Polynomien summa, kuten tehdään, esimerkkejä, harjoituksia

Se Polynomien summa Operaatio koostuu kahden tai useamman polynomin lisäämisestä, mikä johtaa toiseen polynomiin. Sen toteuttamiseksi on tarpeen lisätä kunkin polynomin saman järjestyksen ehdot ja ilmaista tuloksena oleva summa.

Ensin tarkastelemme lyhyesti "saman järjestyksen ehtojen" merkitystä. Kenen tahansa polynomi koostuu summeista ja/tai ehtojen vähentämisestä.

Kuvio 1. Kahden polynomin lisäämiseksi on tarpeen tilata ne ja vähentää sitten samanlaisia ​​termejä. Lähde: Pixabay + Wikimedia Commons.

Termit voivat olla reaalilukujen ja yhden tai useamman muuttujan tuotteita, esimerkiksi kirjaimilla: 3x² ja -√5.-lla²BC³ Ne ovat termejä.

No, saman järjestyksen ehdot ovat ne, joilla on sama eksponentti tai voima, vaikka niillä voi olla erilainen kerroin.

-Tasa -arvoiset ehdot ovat: 5x³, √2 x³ ja -1/2x³

-Eri tilaukset Termit: -2x^-2, 2xy^-1 ja √6x²ja

On tärkeää pitää mielessä, että vain saman järjestyksen ehdot voidaan lisätä tai vähentää, operaatio, joka tunnetaan vähennys. Muuten summa on yksinkertaisesti jätetty.

Kun saman järjestyksen ehtojen käsite selvennetään, polynomit lisätään näiden vaiheiden seurauksena:

-Tilaus Ensin polynomit, jotka lisätään, kaikki samalla tavalla, joko kasvavat tai vähenevät, toisin sanoen voimien kanssa vähiten suurimpaan tai päinvastoin.

-Saada valmiiksi, Jos sekvenssin virtaa puuttuu.

-Vähentää Samanlaiset termit.

-Osoittaa Tuloksena oleva summa.

[TOC]

Polynomisummaesimerkit

Aloitamme lisäämällä kaksi polynomia yhdellä muuttujalla nimeltään x, Esimerkiksi polynomit p (x) ja q (x) antavat:

P (x) = 2x² - 5x⁴ + 2x -x⁵ - 3x³ +12

Q (x) = x⁵- 25 x + x²

Kuvattujen vaiheiden seurauksena se alkaa tilaamalla ne vähenevästi, mikä on tavallisin tapa:

P (x) = -x⁵- 5x⁴  - 3x³  + 2x² + 2x +12

Se voi palvella sinua: Ympyrän kirjoitettu kulma: Määritelmä, lauseet, esimerkit

Q (x) = x⁵+ x² - 25x

Polynomi Q (x) ei ole valmis, nähdään, että voimat, joissa on eksponentti 4, 3 ja 0. Jälkimmäinen on yksinkertaisesti riippumaton termi, jolla ei ole kirjettä.

Q (x) = x⁵+ 0x⁴ + 0x³ + x² - 25x + 0

Kun tämä vaihe on valmis, he ovat valmiita lisäämään. Voit lisätä samanlaiset termit ja ilmaista sitten summan tai sijoittaa toistensa tilaamat polynomit ja vähentää sarakkeilla tällä tavalla:

- x⁵ - 5x⁴  - 3x³ + 2x² + 2x +12

+ x⁵ + 0x⁴ + 0x³  +  x²  - 25x + 0     +

--

0x⁵-5x⁴ - 3x³  +3x² - 23x + 12 = p (x) + q (x)

On tärkeää huomata, että lisättynä se tehdään algebrallisesti merkintöjen sääntöjen kunnioittamiseksi, tällä tavalla 2x + (-25 x) = -23x. Toisin sanoen, jos kertoimilla on erilainen merkki vähennetään ja tulos sisältää merkin pääaineen.

Lisää kaksi tai useampia polynomeja, joissa on useampi kuin yksi muuttuja

Kun kyse on polynomeista, joissa on useampi kuin yksi muuttuja, yksi niistä valitaan tilaamaan sen. Oletetaan esimerkiksi, että sitä pyydetään lisää:

R (x, y) = 5x²  - 4y² +  8xy - 6y³ 

JA:

T (x, y) = ½ x²- 6y²  - 11xy + x³ja

Yksi muuttujista valitaan, esimerkiksi x tilaukseen:

R (x, y) = 5x² +  8xy - 6y³  - 4y²

T (x, y) = + x³y + ½ x² - 11xy - 6y² 

Puuttuvat ehdot saadaan heti päätökseen, minkä mukaan jokaisella polynomilla on:

R (x, y) = 0x³ja + 5x² +  8xy - 6y³  - 4y²

T (x, y) = + x³y + ½ x² - 11xy + 0y³ - 6y² 

Ja molemmat ovat valmiita vähentämään samanlaisia ​​termejä:

0x³ja + 5x² +  8xy - 6y³  - 4y²

Voi palvella sinua: Määrityskerroin: kaavat, laskenta, tulkinta, esimerkkejä

+ x³y + ½ x² - 11xy + 0y³ - 6y²       +

-

+ x³Y + 11/2x² - 3xy - 6y³  - 10y²    = R (x, y) + t (x, y)

Polynomisummaharjoitukset

- Harjoitus 1

Ilmoita seuraavassa polynomien summassa termi, jonka on mentävä tyhjään saamaan polynomisumma:

-5x⁴  + 0x³ +  2x²         + 1

x⁵  + 2x⁴             - 21x² + 8x - 3

2x⁵             +9x³             -14x

-

-6x⁵+10x⁴ -0x³  + 5x²   - 11x + 21

Ratkaisu

Saada -6x⁵ Vaaditaan kirvesmuodon termi⁵, sellainen:

A + 1+ 2 = -6

Siksi:

A = -6-1-2 = -9

Ja haettava termi on:

-9x⁵

-Jatka samalla tavalla löytääksesi loput termit. Tässä on eksponentti 4:

-5 + 2 + A = 10 → A = 10 + 5-2 = 13

Puuttuva termi on: 13x⁴.

-X Powersille³ On välitöntä, että termin on oltava -9x³, Tällä tavoin kuutiotermi -kerroin on 0.

-Mitä neliövoimiin: A + 8 -14 = -11 → A = -11 -8 + 14 = -5 ja termi on -5x².

-Lineaarinen termi saadaan A +8 -14 = -11 → A = -11 + 14 -8 = -5, puuttuva termi -5x.

-Lopuksi, riippumaton termi on: 1 -3 + a = -21 → a = -19.

- Harjoitus 2

Litteä maasto ympäröi kuvassa esitetyllä tavalla. Löydä ilmaus:

a) kehä ja

b) sen pinta -ala ilmoitettujen pituuksien suhteen:

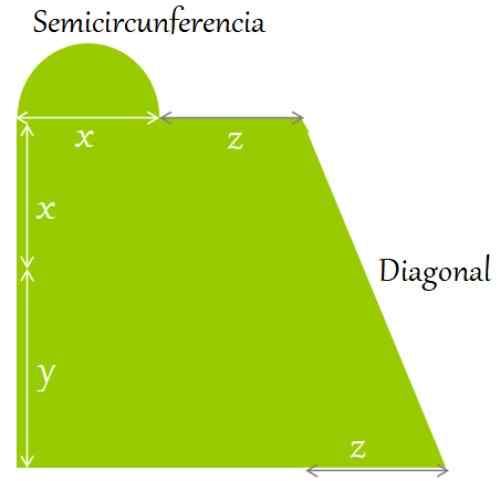Kuva 2. Litteistä maastoa ympäröivät ilmoitetut muodot ja mitat. Lähde: f. Zapata.

Liittää jhk

Kehä on määritelty kuvan sivujen ja muodon summana. Alkaen vasemmasta alakulmasta, kellon käsien suuntaan, sinulla on:

Se voi palvella sinua: ISCELES Trapezoid: Ominaisuudet, suhteet ja kaavat, esimerkit

Kehä = y + x + puolipyöreä pituus + z -z + diagonaalipituus + Z + z + x

Puolipyörän halkaisija on yhtä suuri kuin x. Koska säde on puolet halkaisijasta, sen on:

Radio = x/2.

Kaava täydellisen ympärysmittaisen pituuden kannalta on:

L = 2π x -radio

Niin:

Puolipyörän pituus = ½. 2π (x/2) = πx/2

Diagonaali puolestaan ​​lasketaan sivuille sovelletulla pythagoras -lauseella: (x+y), joka on pystysuora puoli ja Z, joka on vaakasuora:

Diagonaali = [(x+y)² + z -z²-^1/2

Nämä lausekkeet korvataan kehällä saadakseen:

Kehä = y + x + πx/2 + z + [(x + y)² + z -z²-^1/2+ z + x + z

Samankaltaiset termit vähenevät, koska summa edellyttää, että tulosta yksinkertaistetaan maksimiin:

Kehä = y + [x + π (x/2) + x] + z + z + z + [(x + y)² + z -z²-^1/2 = y + (2 + π /2) x + 3Z

Ratkaisu b

Tuloksena oleva alue on suorakulmion alueen, puolipyörän ja oikean kolmion summa. Näiden alueiden kaavat ovat:

-Suorakulmio- Pohja x korkeus

-Puolipyöreä- ½ π (radio)²

-Kolmio- Pohja x korkeus /2

Suorakulmioalue

(x+y). (x+z) = x² + Xz + yx + yz

Puolipyöreä alue

½ π (x/2)² = π x² / 8

Kolmion alue

½ z (x + y) = ½ zx + ½ zy

Kokonaisalue

Kokonaispinta -alan löytämiseksi lisätään jokaiselle osittaiselle alueelle löydetyt lausekkeet:

Kokonaispinta -ala = x² + Xz + yx + yz + (π x² / 8) + ½ zx + ½ zy

Ja lopuksi kaikki samanlaiset termit:

Kokonaispinta -ala = (1 + π/8) x² + 3/2 xy + 3/2yz + yx

Viitteet

1. Baldor, a. 1991. Algebra. Venezuelan kulttuuritoimitus S.-Lla.
2. Jiménez, r. 2008. Algebra. Prentice Hall.
3. Matematiikka on hauskaa. Lisääminen ja vähentäminen polynomit. Toipunut: MathSisfun.com.
4. Monterey Institute. Polynomien lisääminen ja vähentäminen. Toipunut: Montereyinstitute.org.
5. UC Berkeley. Polynomien algebra. Toipunut: matematiikka.Berkeley.Edu.