Teleskooppinen kesä kuinka se on ratkaistu ja ratkaistava harjoitus

Se summaus Teleskooppinen Se on operaatiohaara numeerisella sarjalla. Käsittelee elementtien yhteenvetoja alkuperäisestä arvosta "n" lausekkeisiin, joiden argumentti johtuu mistä tahansa seuraavista malleista:

(F_x - F_x+1); F_x+1  - F_x-A

Missä sen yhteenveto ilmaisu määritellään seuraavasti: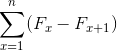

Yhtä hyvin:

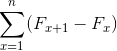
Lähde: Pixabay.com

Ne edustavat summaa elementtejä, jotka kehitettäessä peruutetaan vastakkaiset ehdot. Aiheuttaen seuraavan tasa -arvon teleskooppisia summauksia:

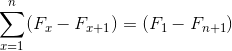
Sen nimi tulee suhteesta klassisen kaukoputken esiintymiseen, joka voitaisiin taittaa ja ottaa käyttöön, muuttaen merkittävästi sen ulottuvuutta. Samoin teleskooppiset summaukset, jotka ovat luonteeltaan äärettömiä, voidaan tiivistää yksinkertaistetussa ilmaisussa:

F₁ - F_N+1

[TOC]

Esittely

Ehtojen summan kehitettäessä tekijöiden poistaminen on melko ilmeistä. Jos jokaisessa tapauksessa vastakkaiset elementit ilmestyvät seuraavaan iteraatioon.

Ensimmäistä tapausta pidetään esimerkkinä (f_x - F_x+1), koska prosessi toimii homologisena (F_x+1-F_x-A.

Kolmen ensimmäisen arvon kehittäminen 1, 2, 3 Yksinkertaistaminen on havaittu

X₁     (F₁ - F₁₊₁) = F₁ - F₂

X₂     (F₂ - F₂₊₁) = F₂ - F₃

X₃     (F₃ - F₃₊₁) = F₃ - F₄

Missä ilmaisemalla kuvattujen elementtien summa:

X₁ + X₂ + X₃ = F₁ - F₂ + F₂ - F₃ + F₃ - F₄

Havaitaan, että termit f₂ ja f₃ Heitä kuvataan vastakohtiensa kanssa, mikä tekee heidän yksinkertaistamisestaan ​​väistämättömän. Samoin havaitaan, että termit f₁ ja f₄ jäädä jäljelle.

Jos summa tehtiin kohdasta x = 1 - x = 3, se tarkoittaa sitä elementtiä f₄ vastaa yleistä termiä f_N+1.

Siten tasa -arvon osoittaminen:

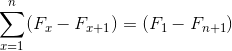
Kuinka se ratkaistaan?

Teleskooppisten summausten tarkoituksena on helpottaa työtä, joten ei ole tarpeen kehittää ääretöntä määrää termejä tai yksinkertaistaa joitain liian pitkäketjuja.

Voi palvella sinua: Trachtenberg -menetelmä: Mikä se on, esimerkkejä

Päätöslauselmaa varten on tarpeen vain arvioida termejä f₁ ja f_N+1. Nämä yksinkertaiset substituutiot muodostavat summan lopputuloksen.

Ehtojen kokonaisuutta ei ilmaista, ja siitä tulee välttämätöntä tuloksen osoittamiseksi, mutta ei normaalille laskentaprosessille.

Tärkeää on huomata numeerisen sarjan lähentyminen. Joskus summan väitettä ei ilmaista teleskooppisella tavalla. Näissä tapauksissa vaihtoehtoisten tekijämenetelmien toteuttaminen on hyvin yleistä.

Tyypillinen faktorisointimenetelmä teleskooppisissa yhteenvedoissa on yksinkertaiset fraktiot. Tämä tapahtuu, kun alkuperäinen fraktio hajoaa useiden fraktioiden summaksi, missä teleskooppikuvio voidaan havaita (F_x - F_x+1) tai (f_x+1  - F_x-A.

Hajoaminen yksinkertaisissa fraktioissa

Numeerisen sarjan lähentymisen varmistamiseksi on hyvin yleistä muuttaa rationaalisia lausekkeita yksinkertaisella fraktiomenetelmällä. Tavoitteena on mallintaa argumentti teleskooppisen summauksen muotoon asti.

Esimerkiksi seuraava tasa -arvo edustaa hajoamista yksinkertaisissa fraktioissa:

Kun kehitetään numeerisia sarjoja ja soveltaa vastaavia ominaisuuksia, lauseke vie seuraavasti:

Missä teleskooppimuoto voidaan nähdä (F_x - F_x+1-A.

Menettely on melko intuitiivinen ja koostuu osoittajan arvojen löytämisestä, jotka katkaisematta tasa -arvoa sallivat nimittäjän tuotteiden erottamisen. Yhtälöt, jotka syntyvät näiden arvojen määrittämisessä, nostetaan tasa -arvon molemmin puolin vertailujen mukaan.

Tätä menettelyä havaitaan askel askeleelta harjoituksen 2 kehittämisessä.

Voi palvella sinua: 6 hauskaa matemaattista arvoitusta lapsille

Historia

On melko epävarmaa pystyä määrittelemään historiallinen hetki, jolloin teleskooppiset summaukset esitettiin. Sen toteutus alkaa kuitenkin nähdä 1700 -luvulla, Leibnizin ja Huygensin suorittamien numeeristen sarjojen tutkimuksissa.

Molemmat matemaatikot, kun tutkitaan kolmion lukumäärän summauksia, alkavat huomata tiettyjen peräkkäisten elementtien konvergenssin suuntauksia. Mutta vielä mielenkiintoisempi on näiden ilmaisujen mallinnuksen alku elementeissä, joita ei välttämättä tapahdu.

Itse asiassa lauseke, jota aiemmin käytettiin viittaamaan yksinkertaisiin fraktioihin:

Sen esittelivät Huygens ja kutsui heti Leibnizin huomion. Kuka ajan myötä voi tarkkailla lähentymistä arvoon 2. Tietämättä sitä, se toteutti teleskooppisen summauksen.

Harjoitukset

Harjoitus 1

Määritä, mikä termi seuraava summa lähenee:

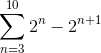
Kun summa kehitetään manuaalisesti, havaitaan seuraava kuvio:

(2³ - 2⁴) + (2⁴ - 2⁵) + (2⁵ - 2⁶)… (2¹⁰ - 2^yksitoista-A

Missä tekijät 2⁴ enintään 2¹⁰ He esittävät positiivisia ja negatiivisia osia, mikä tekee heidän peruutuksensa ilmeiseksi. Silloin ainoat tekijät, joita ei yksinkertaisteta, ovat ensimmäinen ”2³"Ja viimeinen" 2^yksitoista".

Tällä tavalla se saadaan teleskooppiset yhteenvetokriteerit:

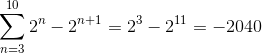
Harjoitus 2

Muuta argumentti teleskooppiseksi tyyppiseksi summaksi ja määritä sarjan lähentyminen:

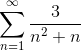
Kuten lausunnossa todetaan, ensimmäinen asia on hajottaa yksinkertaisissa fraktioissa väitteen uudelleenarvioimiseksi ja sen ilmaisemiseksi teleskooppimuodossa.

2 fraktiota, joiden nimittäjät ovat vastaavasti “N” ja “N+1”, on löydettävä, missä alla käytetyn menetelmän on saavutettava tasa -arvoa täyttävän numeraattorin arvot.

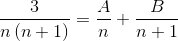
A: n ja B: n arvot on määritelty. Ensimmäinen fraktioiden summa tehdään.

Voi palvella sinua: 60 jakajaa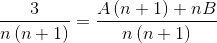

Sitten nimittäjiä yksinkertaistetaan ja lineaarinen yhtälö perustetaan.

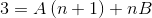
Seuraavassa vaiheessa oikean lausekkeen käyttöä käytetään, kunnes vasemmalla olevan ”3”: n kanssa verrattavissa oleva kuvio.

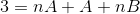
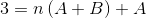
Käytettävien yhtälöiden määrittelemiseksi on verrattava tasa -arvon molemmin puolin tuloksia. Eli vasemmalla puolella ei havaita muuttuvaa N -arvoja, tällä tavalla A +B: n on oltava yhtä suuri kuin nolla.

A + B = 0; A = -b

Toisaalta vakion arvon on oltava yhtä suuri kuin vakioarvo 3.

A = 3

Siksi.

A = 3 ja b = -3

Määritelty jo yksinkertaisten fraktioiden osoitin arvot, summa ajattelee uudelleen.

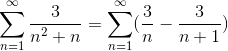
Jos teleskooppisen summauksen yleinen muoto on jo saavutettu. Teleskooppisarja on kehitetty.

Jos jakamalla erittäin suurella määrällä tulos lähtee yhä enemmän, sarjan lähentymisen havaitseminen arvoon 3.

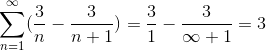
Tämän tyyppisiä sarjoja ei voitu ratkaista, toisin sanoen, johtuen ongelman määrittelemästä äärettömästä määrästä iteraatioita. Tämä menetelmä yhdessä monien muiden kanssa kehystetään kuitenkin numeeristen sarjojen tutkimuksen haara, jonka tavoitteena on määrittää lähentymisarvot tai määritellä näiden sarjojen erottelu.

Viitteet

1. InfinitSimaaliset laskentatunnit. Manuel Franco, Manuel Franco Nicolás, Francisco Martínez González, Roque Molina Legaz. Editum, 1994.
2. Kattava laskelma: peräkkäiset ja toimintojen sarjat. Antonio Rivera figueroa. Patria -toimitusryhmä, 21. lokakuuta. 2014.
3. Kurssi laskennassa ja todellisessa analyysissä. Sudhir r. Ghorpade, Balmohan V. Limaye. Springer Science & Business Media, 5. kesäkuuta. 2006.
4. Ääretön sarja. Tomlinson Fort. Clarendon Press, 1930.
5. Äärettömien kulkueiden teorian elementit. Lloyd Leroy Smail. McGraw-Hill Book Company, Incorpan, 1923.