Sarjojen ominaisuudet, elementit, esimerkit, harjoitukset

Se asettaa teoria Se on logiikan matematiikan haara, joka vastaa joukkojen välisten suhteiden tutkimisesta, jota kutsutaan joukkoiksi. Sarjoille on ominaista olla saman luonteenotokonekokoelmia. Nämä esineet ovat sarjan elementtejä ja voivat olla: numerot, kirjaimet, geometriset luvut, objektit, esineet itse ja muut.

Georg Cantor, 1800 -luvun loppua kohti, ehdotti sarjoja. Vaikka muut merkittävät matemaatikot 2000 -luvulla tekivät muodollisuutensa: Gottlob Frege, Ernst Zermelo, Bertrand Russell, Adolf Fraenkel muun muassa.

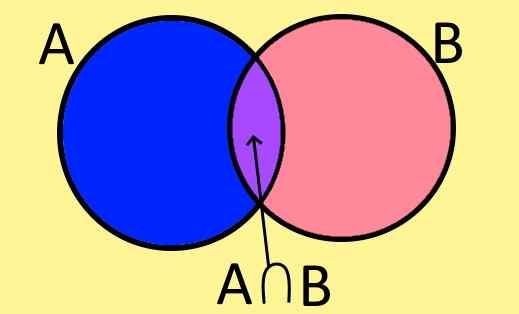
Kuvio 1. Venn -kaavio sarjoista A, B ja niiden risteys A⋂ B. (Oma yksityiskohta).

Venn -kaaviot ovat graafinen tapa edustaa sarjaa, ja ne koostuvat suljetusta tasaisesta hahmosta, jonka sisällä sarjan elementit ovat.

Esimerkiksi, kuvio 1 näyttää kaksi sarjaa A ja B, joilla on yhteisiä elementtejä, A: lle ja B: lle yhteiset elementit. Nämä muodostavat uuden sarjan nimeltä A ja B risteysjoukko, joka on kirjoitettu symbolisesti seuraavasti:

A ∩ B

[TOC]

Ominaisuudet

Sarja on primitiivinen käsite, koska se on geometriassa pisteen, suoran tai litteän käsite. Ei ole parempaa tapaa ilmaista konseptia kuin osoittaa esimerkkejä: 

Sarja ja muodostettu Espanjan lipun värit. Tätä tapaa ilmaista sarjaa kutsutaan ymmärtämällä. Sama ja laajennuksen kirjoittanut on:

E = punainen, keltainen

Tässä tapauksessa punainen ja keltainen ovat asetettuja elementtejä. On huomattava, että elementit on lueteltu avaimien välillä eikä niitä toisteta. Espanjan lipun tapauksessa on kolme väriraitaa (punainen, keltainen, punainen), joista kaksi toistetaan, mutta elementtejä ei toisteta, kun sarja ilmaistaan.

Oletetaan, että asetetaan kolme ensimmäistä äänekirjettä:

V = a, e, i

V: n voima, jota P (V) on merkitty, on joukko sarjoja, jotka voidaan muodostaa V: n:

P (v) = a, e, i, a, e, a, i, e, i, a, e, i

Sarjojen tyypit

Rajallinen sarja

Se on sarja, jossa sen elementit ovat lukuisia. Esimerkkejä äärellisistä sarjoista ovat espanjalaisen aakkosten, espanjalaisten, aurinkokunnan planeettojen kirjeitä. Äärellisen sarjan elementtien lukumäärää kutsutaan sen kardinaalisuudelle.

Ääretön sarja

Ääretön yhtye, kaikki sen elementtien lukumäärä on käsittämätön, koska riippumatta siitä, kuinka suuri sen elementtien lukumäärä on aina mahdollista löytää lisää elementtejä.

Äärettömä joukko esimerkki on luonnonlukujen n joukko n, joka ilmaistaan ​​laajasti seuraavasti:

Voi palvella sinua: Coplanares -pisteet: Yhtälö, esimerkki ja ratkaisut harjoitukset

N = 1, 2, 3, 4, 5, .. . on selvästi ääretön sarja, koska sillä ei ole väliä kuinka suuri luonnollinen luku voi olla, seuraava pääaine voi aina löytää loputtomassa prosessissa. Selvästi äärettömän sarjan kardinaalisuus on ∞.

Tyhjä sarja

Se on sarja, joka ei sisällä mitään elementtiä. Tyhjä sarja V merkitään Ø: llä tai näppäinparin avulla ilman elementtejä:

V = = Ø.

Tyhjä sarja on ainutlaatuinen, joten on oltava virheellistä sanoa "tyhjä sarja", oikea muoto on sanoa "tyhjä sarja".

Tyhjän sarjan ominaisuuksien joukossa on, että se on minkä tahansa sarjan osajoukko:

Ø ⊂ a

Lisäksi, jos sarja on tyhjän sarjan osajoukko, tämä sarja on välttämättä tyhjä:

A ⊂ Ø ⇔ A = Ø

Yhtenäinen sarja

Sitä kutsutaan yhtenäiseksi sarjaksi, joka sisältää yhden elementin. Esimerkiksi maan luonnollisten satelliittien sarja on yksikköjoukko, jonka ainoa elementti on kuu. Asetettu kokonaisluku, joka on pienempi kuin 2 ja suurempi kuin nolla, on vain elementti 1, joten se on yksikköjoukko.

Binaarisarja

Sarja on binaarinen, jos siinä on vain kaksi elementtiä. Esimerkiksi sarja X, niin x on todellinen lukumäärä x^2 = 2 = 2. Tämä laajennuksen sarja on kirjoitettu seuraavasti:

X = -√2, +√2

Yleinen sarja

Universal -sarja on sarja, joka sisältää muita samantyyppisiä tai luontojoukkoja. Esimerkiksi luonnonlukujen yleinen joukko on reaalilukujen joukko. Mutta todelliset numerot ovat myös yleisiä kokonaislukuja ja rationaalisia lukuja.

Ydinasiat

- Suhteet sarjojen välillä

Sarjoissa voit luoda monentyyppisiä suhteita niiden ja niiden elementtien välillä. Jos kahdella sarjassa A ja B on täsmälleen samat elementit, niiden joukossa, yhtäläiset suhteet merkitään seuraavasti:

-Lla = B -

Jos kaikki A -sarjan elementit kuuluvat joukkoon B, mutta kaikki B: n elementit eivät kuulu A: iin, näiden joukossa on sisällyttämissuhde, joka on merkitty seuraavasti:

A ⊂ b, mutta b ⊄ a

Edellinen lauseke lukee: A on B: n osajoukko, mutta B ei ole A: n osajoukko.

Osoittaa, että jotkut tai jotkut elementit kuuluvat joukkoon, käytetään kuulumisen symbolia ∈, esimerkiksi sanoa, että X -elementti tai elementit kuuluvat joukkoon A kirjoitetaan symbolisesti seuraavasti:

x ∈ A

Kyllä, elementti eikä kuulu tähän suhteeseen, on kirjoitettu näin:

ja ∉ a

Kuulumissuhde annetaan sarjan ja sarjan elementtien välillä, lukuun ottamatta voimajoukkoa, sarja on kaikkien mahdollisten sarjojen kokoelma tai sarja, joka voidaan muodostaa mainitun sarjan elementeillä.

Voi palvella sinua: tekijä

Oletetaan, a, e, i, siinä tapauksessa sarjasta V tulee sarjan P (v) elementti ja se voidaan kirjoittaa:

V ∈ P (v)

- Osallisuusominaisuudet

Ensimmäinen osallisuusominaisuus osoittaa, että jokainen sarja on sinänsä tai toisin sanoen, mikä on itsessään osajoukkoa:

A ⊂ a

Toinen sisällyttämisen ominaisuus on transitiivisuus: jos A on B: n ja B: n osajoukko puolestaan, se on C: n osajoukko, niin A on C: n osajoukko. Symbolisesti transitiivisuussuhde on kirjoitettu näin:

(A ⊂ b) ^ (b ⊂ c) => a ⊂ c

Alla on Venn -kaavio, joka vastaa sisällyttämisen transitiivisuutta:

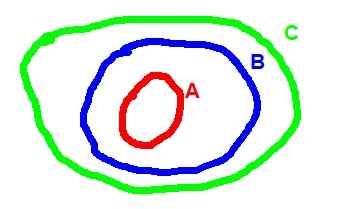Kuva 2. (A ⊂ b) ^ (b ⊂ c) => a ⊂ c

- Operaatio sarjojen välillä

Risteys

Risteys on kahden sarjan välinen operaatio, joka johtaa uuteen sarjaan, joka kuuluu samaan kahden ensimmäisen sarjan sarjaan. Tässä mielessä se on suljettu toiminta.

Symbolisesti leikkausoperaatio on muotoiltu seuraavasti:

A⋂b = x / x∈A ^ x∈B

Esimerkki on seuraava: Aseta sanan "elementit" kirjaimien A ja sanan "toistuvan" kirjaimien asetus B, A: n ja B: n välinen risteys on kirjoitettu näin:

A⋂b = e, l, m, n, t, s ⋂ r, e, p, t, i, d, o, s = e, t, s . A: n ja A⋂ B: n yleismaailmallinen sarja on espanjalaisen aakkosten kirjaimia.

liitto

Kahden sarjan liitto on sarja, jonka muodostavat kahden sarjan kahdelle sarjalle yhteiset elementit. Sarjojen välinen ammattiliitto ilmaistaan ​​symbolisesti seuraavasti:

A∪b = x/x∈A v x∈B

Ero

Ainakin sarjan toiminta on merkitty A-B: llä. A-B on uusi sarja, jonka kaikki elementit ovat A: ssa ja jotka eivät kuulu B: hen. Symboli on kirjoitettu näin:

A - B = x/ x ∈ A ^ x ∉ B

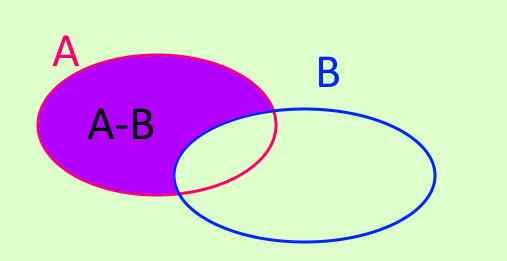Kuva 3. A - B = x/ x ∈ A ^ x ∉ B

Symmetrinen ero

Symmetrinen ero on toiminta kahden sarjan välillä, joissa tuloksena oleva joukko koostuu elementeistä, jotka eivät ole yhteisiä kahdelle sarjalle. Symmetrinen ero symbolisesti esitetään seuraavasti:

A⊕b = x/ x∈ (a-b) ^ x∈ (b-a)

Esimerkit

Esimerkki 1

Venn -kaavio on graafinen tapa edustaa sarjoja. Esimerkiksi sanasarjan kirjaimien asetus on esitetty seuraavasti:

Esimerkki 2

Se on esitetty Venn -kaavioiden avulla, että sanan "asetettu" vokaalien joukko on sanan "asetettu" kirjaimien osajoukko "asetettu".

Voi palvella sinua: kiintiön näytteenotto: menetelmä, edut, haitat, esimerkit

Esimerkki 3

Aseta Ñ Espanjan aakkosten kirjaimista se on äärellinen sarja, tämä laajamittainen joukko on kirjoitettu näin:

Ñ = A, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, w, w, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, X, Y, Z ja sen kardinaalisuus on 27.

Esimerkki 4

Aseta V Espanjan vokaalista se on osa ñ -sarjaa:

V ⊂ Ñ Siksi se on rajallinen sarja.

Rajallinen sarja V Laajennettu tapa, jolla se on kirjoitettu näin: V = a, e, i, o, u ja sen kardinaali on 5.

Esimerkki 5

Ottaen huomioon sarjat a = 2, 4, 6, 8 ja b = 1, 2, 4, 7, 9 Määritä A-B ja B-A. 

A - B ovat elementtejä, joista ne eivät ole B:

A - B = 6, 8

B - A ovat B: n elementtejä, jotka eivät ole A:

B - A = 1, 7, 9

Ratkaisut

Harjoitus 1

Kirjoita symbolisesti ja myös laajentamalla teräslehden P, joka on jopa 10 alle 10 -vuotiaita.

Ratkaisu: P = x∈ N / x < 10 ^ x mod 2 = 0

P = 2, 4, 6, 8

Harjoitus 2

Oletetaan, että kokonaisuus muodostuu luonnollisista luvuista, jotka ovat 210 tekijöitä, ja sarjan B, jotka muodostuvat luonnollisten lukujen serkkujen kanssa alle 9. Määritä molemmat sarjat laajennuksen mukaan ja määritä, mikä suhde on kahden sarjan välillä.

Ratkaisu: Sarjan A elementtien määrittämiseksi sinun on aloitettava löytämällä luonnollisen numeron 210 tekijät:

210 = 2 * 3 * 5 * 7

Sitten asetettu A on kirjoitettu:

A = 2, 3, 5, 7

Tarkastelemme Set B: tä, joka on alle 9 -serkut. 1 ei ole serkku, koska se ei täytä serkkun määritelmää: "Luku on serkku vain ja vain jos siinä on tarkalleen kaksi jakajaa 1 ja itse numero". 2 on tasainen ja samaan aikaan serkku, koska se täyttää serkkun määritelmän, muut serkut, jotka ovat alle 9, ovat 3, 5 ja 7. Joten se joukko B on:

B = 2, 3, 5, 7

Siksi nämä kaksi sarjaa ovat samat: a = B -.

Harjoitus 3

Määritä sarja, jonka elementit x eroavat x: stä.

Ratkaisu: C = x / x ≠ x

Kuten mikä tahansa elementti, numero tai objekti on yhtä suuri kuin itse, asetettu C ei voi olla muu kuin tyhjä sarja:

C = Ø

Harjoitus 4

Olla luonnonlukujen n joukko ja z kokonaislukujoukko. Määritä n ⋂ z y n ∪ z.

Ratkaisu: 

N ⋂ z = x ∈ Z / x ≤ 0 = (-∞, 0]

N ∪ z = z, koska n ⊂ z.

Viitteet

1. Garo, m. (2014). Matematiikka: neliömäiset yhtälöt: Kuinka ratkaista neliömäinen yhtälö. Marilù garo.
2. Haeussler, E. F., & Paul, r. S. (2003). Matematiikka hallinto- ja taloustieteelle. Pearson -koulutus.
3. Jiménez, J., Rodríguez, M., Estrada, r. (2005). Matematiikka 1. syyskuuta. Kynnys.
4. Arvokas, c. T. (2005). Matematiikkakurssi 3o. Toimitusohjelma.
5. Matematiikka 10 (2018). "Esimerkkejä äärellisistä sarjoista". Haettu osoitteesta: matematiikka10.netto
6. Wikipedia. Asettaa teoria. Palautettu: on.Wikipedia.com