Chebyshov -lause, joka on, sovellukset ja esimerkit

Hän Chebyshov -lause (tai Chebyshovin eriarvoisuus) on yksi todennäköisyysteorian tärkeimmistä klassisista tuloksista. Se mahdollistaa satunnaismuuttujan X suhteen kuvattujen tapahtuman todennäköisyyden arvioinnin tarjoamalla meille tason, joka ei riipu satunnaismuuttujan jakautumisesta, vaan X: n varianssista.

Lause kutsutaan venäläisen matemaattisen kunniaksi.

Tätä eriarvoisuutta tai niitä, joita niiden ominaisuuksista kutsutaan Chebyshovin eriarvoisuudeksi, käytetään pääasiassa arvioitujen todennäköisyyksien arviointiin laskentatasojen avulla.

Mikä on chebyshovin lause?

Todennäköisyysteorian tutkimuksessa tapahtuu, että jos tiedetään satunnaismuuttujan X jakautumisfunktio, sen odotettu arvo voidaan laskea - tai matemaattinen toivo ja (x) - ja sen varianssi var (x), niin kauan kuin nämä määriä on olemassa. Vastavuoroinen ei kuitenkaan välttämättä ole totta.

Toisin sanoen E (x): n ja var (x): n tietäminen ei välttämättä saa X: n jakautumisfunktiota, joten määriä, kuten p (| x |> k) joillekin k> 0, on erittäin vaikea saada. Mutta Chebyshovin epätasa -arvon ansiosta on mahdollista arvioida satunnaismuuttujan todennäköisyys.

Chebyshovin lause kertoo meille, että jos meillä on satunnaismuuttuja X näytetilassa todennäköisyysfunktio P, ja jos k> 0, niin: niin:

Voi palvella sinua: Acutlangle Triangle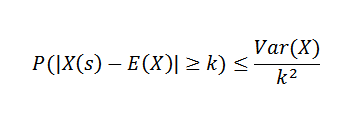

Sovellukset ja esimerkit

Niistä monista sovelluksista, joita Chebyshovin lause hallussaan, seuraavat voidaan mainita:

1. Todennäköisyysraja

Tämä on yleisin sovellus ja sitä käytetään antamaan ylemmän tason P (| x-e (x) | ≥k), jossa k> 0, vain satunnaismuuttujan X varianssin ja toivon kanssa tietämättä todennäköisyysfunktiota.

Esimerkki 1

Oletetaan.

Jos tiedetään, että tuotantoviikon varianssi on yhtä suuri kuin 25, mitä voimme sanoa todennäköisyydestä, että tällä viikolla tuotanto eroaa yli 10 keskimäärin?

Ratkaisu

Chebyshovin epätasa -arvon soveltaminen:

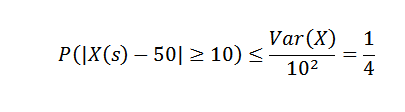
Tästä voimme saada todennäköisyyden, että tuotantoviikolla tavaroiden lukumäärä ylittää yli 10 keskiarvoon, on korkeintaan 1/4.

2. Rajalauseiden osoittaminen

Chebyshovin epätasa -arvolla on tärkeä rooli tärkeimpien rajojen osoittamisessa. Esimerkiksi meillä on seuraavat:

Heikko laki, jossa on suuria määriä

Tämä laki osoittaa, että annetaan peräkkäin x1, x2, ..., xn, ... riippumattomia satunnaismuuttujia, joilla on sama keskimääräinen jakauma e (xi) = μ ja varianssi var (x) = σ², ja tunnettu keskimääräinen näyte:

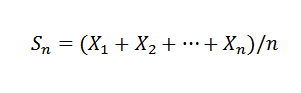
Joten k> 0: lle sinun täytyy:

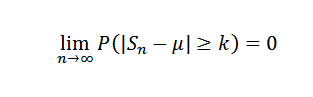
Tai vastaava:

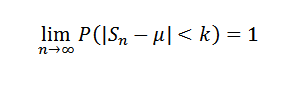
Esittely

Ensin huomaamme seuraavan:

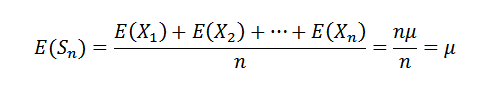
Kuten x1, x2, ..., xn ovat riippumattomia, se seuraa sitä:

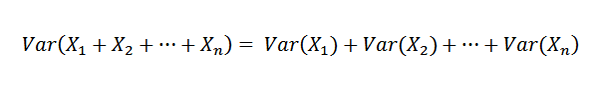
Siksi seuraava on vahvistaa:

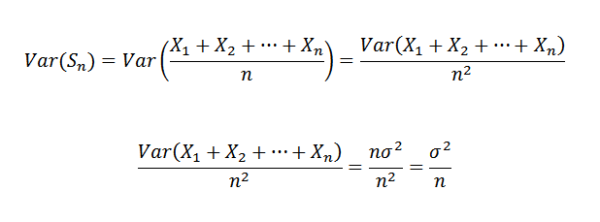
Sitten käyttämällä Chebyshovin lausetta, jolloin sinun on:

Se voi palvella sinua: trigonometriset toiminnot: Basic, Cartesian tasossa, esimerkkejä, liikunta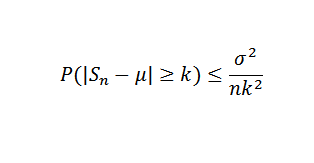

Lopuksi lause johtuu siitä, että oikea raja on nolla, kun n on taipumus äärettömyyteen.

On huomattava, että tämä testi tehtiin vain siinä tapauksessa, jossa XI: n varianssi on; eli se ei eroa. Siten havaitsemme, että lause on aina totta, jos E (xi) on olemassa.

Chebyshovin rajalause

Jos x1, x2, ..., xn, ... se on riippumattomien satunnaismuuttujien peräkkäin siten, että C0 on:

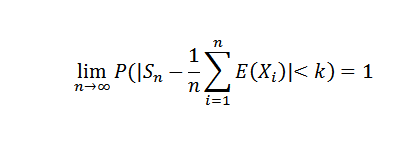
Esittely

Koska varianssien peräkkäisyys on tasaisesti rajoitettu, meillä on se var (sn) ≤ c/n, kaikille luonnollisille n. Mutta tiedämme sen:

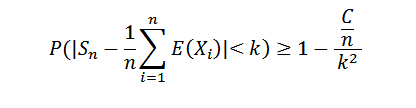
N: n tekeminen äärettömyyteen, se on seuraava:

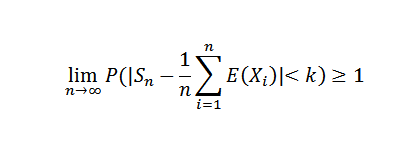
Koska todennäköisyys ei voi ylittää arvoa 1, haluttu tulos saadaan. Tämän lauseen seurauksena voisimme mainita Bernoullin erityistapauksen.

Jos koe toistetaan itsenäisesti kahdella mahdollisella tuloksella (epäonnistuminen ja menestys), missä P on menestyksen todennäköisyys kussakin kokeessa ja x on satunnaismuuttuja, joka edustaa saatujen menestysten lukumäärää, niin jokaiselle k> 0: lle sinun on:

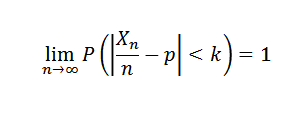
3. Otoskoko

Varianssin kannalta Chebyshovin epätasa-arvo antaa meille mahdollisuuden löytää näytteen koon, joka riittää varmistamaan, että todennäköisyys, että | sn-μ | keskiverto.

Tarkalleen, olipa se sitten x1, x2, ... xn Näyte riippumattomista satunnaismuuttujista, joiden koko on N -kokoinen, ja oletetaan, että e (xi) = μ ja sen varianssi σ². Joten Chebyshovin epätasa -arvon vuoksi sinun on:

Voi palvella sinua: Euler -numero tai numero E: Kuinka paljon OK, ominaisuudet, sovellukset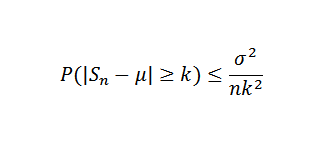

Nyt Δ> 0 kiinteä. Meidän täytyy:

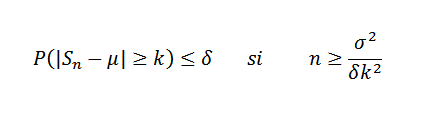
Esimerkki

Oletetaan, että x1, x2, ... xn ovat näyte riippumattomista satunnaismuuttujista, joissa on Bernoulli -jakauma, niin että ne ottavat arvon 1 todennäköisyydellä P = 0.5.

Mikä on näytteen koko varmistaa, että todennäköisyys, että ero aritmeettisen keskiarvon SN ja sen odotettavissa oleva arvo (joka ylittää yli 0,1), on pienempi tai yhtä suuri kuin 0.,01?

Ratkaisu

Meidän on (x) = μ = p = 0,5 ja mitä var (x) = σ²= P (1-P) = 0,25. Chebyshovin epätasa -arvoon jokaiselle K> 0: lle meidän on:

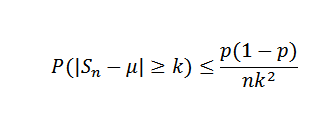
Nyt, kun otat k = 0,1 ja Δ = 0,01, sinun on:

Tällä tavoin tarvitaan, että tarvitaan vähintään 2500 näytteen kokoa sen varmistamiseksi, että tapahtuman todennäköisyys | SN - 0,5 |> = 0,1 on alle 0,01.

Chebyshov -tyyppinen eriarvoisuus

Chebyshovin eriarvoisuuteen liittyy useita eriarvoisuutta. Yksi tunnetuimmista on Markovin epätasa -arvo:

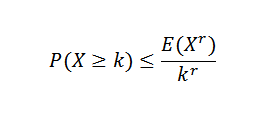
Tässä ekspressiossa X se on ei -negatiivinen satunnaismuuttuja K, r> 0.

Markovin epätasa -arvo voi olla eri muodoissa. Esimerkiksi joko ja ei -negatiivinen satunnaismuuttuja (niin p (y> = 0) = 1) ja oletetaan, että e (y) = μ on olemassa. Oletetaan myös, että (e (y))^{r -}= μ_{r -} Joillekin kokonaislukuille r> 1. Niin:

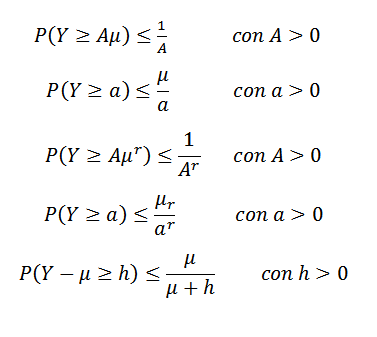
Toinen eriarvoisuus on Gauss, joka kertoo meille, että annetaan yksimodaalinen x -satunnaismuuttuja, jolla on muodissa nolla, sitten k> 0: lle,