Olemassaolon ja ainutlaatuisuuden esittely, esimerkit ja harjoitukset

Hän Olemassaolo- ja ainutlaatuisuuslause määrittää välttämättömät ja riittävät olosuhteet ensimmäisen järjestyksen differentiaaliyhtälölle, tietyllä alkuolosuhteella, jotta saadaan ratkaisu ja että tämä ratkaisu on myös ainoa. 

Lause ei kuitenkaan anna mitään tekniikkaa tai osoitusta sellaisen ratkaisun löytämisestä. Olemassaolo- ja ainutlaatuisuuslause ulottuu myös korkeamman asteen differentiaaliyhtälöihin alkuolosuhteilla, mikä tunnetaan nimellä Cauchy -ongelma.

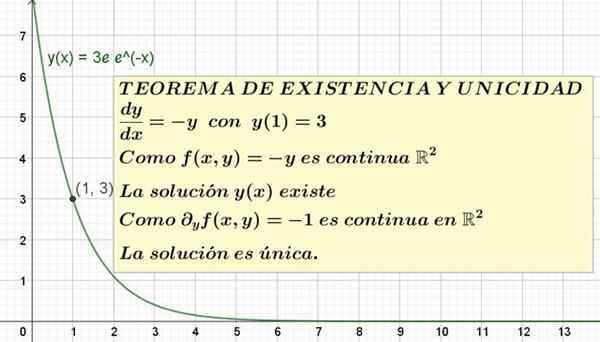
Kuvio 1. Erotusyhtälö, jossa on alkutila ja sen ratkaisu on esitetty. Olemassaolo ja ainutlaatuisuuslause takaavat, että se on ainoa mahdollinen ratkaisu.

Muodollinen lausunto olemassaolosta ja ainutlaatuisuudesta on seuraava:

"Differentiaaliyhtälölle ja '(x) = f (x, y) alkuperäisessä kunnossa ja (a) = b,  olemassa Ainakin yksi liuos tason suorakulmaisella alueella Xy sisältää pisteen (A, b), Joo f (x, y) Se on jatkuvaa tällä alueella. Ja jos osittainen johdannainen F kuin ja: G = ∂f/ ∂y Se on jatkuva samassa suorakulmaisessa alueella, joten ratkaisu on ainutlaatuinen pisteen ympäristössä (A, b) sisältö jatkuvuusalueella F ja g."

Tämän lauseen hyödyllisyys on ensin tietää, mitkä ovat XY -tason alueet, joilla voi olla ratkaisu, ja myös tietää, onko löydetty ratkaisu ainoa mahdollinen vai onko muita. 

Huomaa, että siinä tapauksessa, että ainutlaatuisen kunto.

[TOC]

Olemassaolon ja ainutlaatuisuuden lauseen osoittaminen

Kuva 2. Charles Émile Picardille (1856-1941) Yksi ensimmäisistä olemassaolon ja ainutlaatuisuuden lauseiden esityksistä on akkreditoitu. Lähde: Wikimedia Commons.

Tätä lausetta varten tunnetaan kaksi mahdollista demonstraatiota, joista yksi on Charles Émile Picardin (1856-1941) esittely ja toinen Giuseppe Peano (1858-1932), joka perustuu Augustin Louis Cauchyn (1789-1857 -A.

Voi palvella sinua: samanaikaiset vektorit: ominaisuudet, esimerkit ja harjoitukset

On huomattava, että 1800 -luvun kirkkaimmat matemaattiset mielet osallistuivat tämän lauseen osoittamiseen, joten voi olla intuitia, että kumpikaan niistä ei ole yksinkertainen.

Lauseen muodollisesti osoittamiseksi on ensin perustettava sarja edistyneempiä matematiikkakäsitteitä, kuten Lipschitz -tyyppiset toiminnot, banach -tilat, karatheodory ja useita muita olemassaolelauseita, jotka pakenevat artikkelin tarkoituksesta.

Suuri osa fysiikassa käsiteltyistä differentiaaliyhtälöistä käsittelee mielenkiintoisia alueita jatkuvia toimintoja, joten rajoitamme itsemme osoittamaan tapaa, jolla lausetta sovelletaan yksinkertaisissa yhtälöissä.

Esimerkit

- Esimerkki 1

Harkitse seuraavaa differentiaaliyhtälöä alkuperäisellä ehdoilla:

ja '(x) = - y; kanssa ja (1) = 3

Onko tähän ongelmaan ratkaisu? Onko se ainoa mahdollinen ratkaisu?

Vastaukset

Ensinnäkin arvioidaan differentiaaliyhtälön ratkaisun olemassaolo ja että se täyttää myös alkuperäisen tilan. 

Tässä esimerkissä f (x, y) = - y Olemassaolon kunto vaatii tietämään  f (x, y) Se on jatkuvaa lentokoneessa Xy Sisältää koordinaattipistettä x = 1, y = 3.

Mutta f (x, y) = -y Se on toiminto, joka on jatkuvaa reaalilukujen alueella ja on olemassa koko reaalilukualueella.

Siksi päätellään, että F (x, y) on jatkuvaa R: ssä², Joten lause takaa ainakin yhden ratkaisun olemassaolon.

Tietäen tämän, on aika arvioida, onko ratkaisu ainutlaatuinen vai onko päinvastoin enemmän kuin yksi. Tätä varten on tarpeen laskea osittainen johdannainen F Muuttujan suhteen ja-

∂f/∂y = ∂ (-y)/∂y = -1

Niin G (x, y) = -1 joka on vakio funktio, joka on myös määritelty kaikille r² Ja se on myös jatkuvaa siellä. Tästä seuraa, että olemassaolo- ja ainutlaatuisuuslauseke takaavat, että tällä alkuperäisellä arvoongelmalla on ainutlaatuinen ratkaisu, vaikka se ei kerro meille, mikä se on.

Voi palvella sinua: Conpex Polygon: Määritelmä, elementit, ominaisuudet, esimerkit

- Esimerkki 2

Harkitse seuraavaa ensimmäisen tilauksen tavallista differentiaaliyhtälöä alkuperäisellä ehdoilla:

ja '(x) = 2√y; ja (0) = 0.

Onko ratkaisua ja (x) Tätä ongelmaa? Jos näin on, selvitä, onko yksi tai useampi kuin yksi.

Vastaus

Harkitsemme toimintoa f (x, y) = 2√y. Toiminto F on määritelty vain y ≥0, No, tiedämme, että negatiivisella luvulla puuttuu todellinen juuri. sitä paitsi f (x, y) Se on jatkuvaa r²  mukaan lukien x -akseli, niin Olemassaolo- ja ainutlaatuisuuslauseke takaavat Ainakin yksi ratkaisu kyseisellä alueella.

Alkuolosuhde x = 0, y = 0 on liuosalueen reunalla. Sitten otamme f (x, y) osittaisen johdannaisen suhteessa y:

∂f/∂y = 1/√y

Tässä tapauksessa funktiota ei ole määritelty y = 0: lle, juuri missä alkuolosuhteet ovat.

Mikä kertoo lauseen? Se kertoo meille, että vaikka tiedämme, että on ainakin yksi ratkaisu, X -akselin ylempi puolipilo, mukaan lukien X -akseli, koska ainutlaatuisuuden olosuhteet eivät täyty, ei ole mitään takeita siitä, että yksi ratkaisu on olemassa yksi ratkaisu.

Tämä tarkoittaa, että F (x, y) jatkuvuusalueella voi olla yksi tai useampi ratkaisu,. Ja kuten aina, lause ei kerro meille, mikä voisi olla.

Ratkaisut

- Harjoitus 1

Ratkaise esimerkin 1 cauchy -ongelma:

ja '(x) = - y; kanssa ja (1) = 3. 

Etsi funktio y (x), joka täyttää differentiaaliyhtälön ja alkuolosuhteet.

Ratkaisu

Esimerkissä 1 määritettiin, että tällä ongelmalla on ratkaisu ja se on myös ainutlaatuinen. Ratkaisun löytämiseksi ensimmäinen asia, joka on huomattava, on se, että se on ensimmäinen -asukas erotettavien muuttujien differentiaaliyhtälö, joka on kirjoitettu seuraavasti:

Voi palvella sinua: Variaatiokerroin: Mihin se on, laskenta, esimerkit, harjoitukset

dy /dx = - ja → dy = -y dx

Jakaminen molemmissa jäsenissä ja niiden välillä erottamaan muuttujat:

dy/y = - dx

Molempien jäsenten määrittelemätön integraali on sovellettu:

∫ (1/y) dy = - ∫dx

Määrittelemättömien integraalien ratkaiseminen on:

ln (y) = -x + c

missä C on integraation vakio, joka määritetään alkuperäisen ehdon perusteella:

ln (3) = -1 + C, toisin sanoen C = 1 + ln (3)

C: n ja uudelleenorganisoinnin arvon korvaaminen on:

ln (y) - ln (3) = -x + 1

Seuraavan logaritmien ominaisuuden soveltaminen:

Logaritmien ero on osamäärä logaritmi

Aikaisempi ilmaisu voidaan kirjoittaa uudelleen:

ln (y/3) = 1 - x

Eksponentiaalista funktiota sovelletaan molempien jäsenten kanssa:

Y / 3 = e^{(1 - x)}

Mikä vastaa:

 y = 3e e^-x

Tämä on yhtälön ainutlaatuinen ratkaisu ja '= -y y (1) = 3. Tämän liuoksen kaavio on esitetty kuvassa 1.

- Harjoitus 2

Löydä kaksi ratkaisua esimerkissä 2 esiintyvään ongelmaan:

ja '(x) = 2√ (y); ja (0) = 0.

Ratkaisu

Se on myös yhtälö erillisistä muuttujista, joka on kirjoitettu eri tavalla:

Dy / √ (y) = 2 dx

Määrittelemättömän integraalin ottaminen molemmissa jäsenissä on edelleen:

2 √ (y) = 2 x + c

Kuten tiedetään, että y ≥0 Meillä on ratkaisualueella:

y = (x + c)² 

Mutta koska alkuolosuhde x = 0, y = 0 on täytettävä, niin vakio C on nolla ja seuraava ratkaisu pysyy:

ja (x) = x².

Mutta tämä ratkaisu ei ole ainutlaatuinen, funktio y (x) = 0 on myös ratkaisu nostettuun ongelmaan. Esimerkin 2 ongelmaan sovellettu olemassaolo ja ainutlaatuisuuslause oli jo ennustanut, että ratkaisua voi olla useampi kuin yksi.

Viitteet

1. Coddington, Earl A.; Levinson, Norman (1955), Tavallisten differentiaaliyhtälöiden teoria, New York: McGraw-Hill.
2. Matematiikan tietosanakirja. Cauchy-lipschitz-lause. Palautettu: Encyclopediaofmath.org
3. Lindelöf, South L'A -sovellus Methode des A -likiarvot peräkkäiset Aux Équations Différentielles Ordinaires du Premier Ordre; CompTtes Rendus Hebdomadaires des Séances de l'Anc Acadequie des Sciences. Osa. 116, 1894, s. 454-457. Toipunut: gallic.Bnf.fr.
4. Wikipedia. Picardin peräkkäinen lähestymistapa menetelmä. Palautettu: on.Wikipedia.com
5. Wikipedia. Picard-Lindelöf-lause. Palautettu: on.Wikipedia.com.
6. Zill, D.1986. Alkeis differentiaaliyhtälö sovelluksilla.Prentice Hall.