Vihreä lause, esittely, sovellukset ja harjoitukset

Hän Vihreä lause Se on laskentamenetelmä. Kyseiset toiminnot on osoitettava vektori- ja määriteltyinä kentinä radalla C.

Esimerkiksi integraalilinjan ilmaisu voi olla erittäin monimutkainen ratkaista; Greenin lauseen toteuttamisessa kaksinkertaiset integraalit muuttuvat kuitenkin melko perusteellisiksi. On aina tärkeää kunnioittaa etenemissuunnan positiivista merkitystä, tämä viittaa kelloneulojen suuntaan.

Greenin lause on erityinen tapaus Stokesin lauseesta, jossa vektorifunktion projektio suoritetaan XY -tasossa.

[TOC]

Määritelmä

Greenin ilmaus Greenin lauseesta on seuraava:

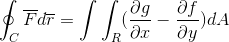
Ensimmäisellä termillä havaitaan linja -integraali, joka on määritelty radalla "C", tuotehenklin "F" ja vektorin "r" välisen tuotehenkilöstön välillä "r".

C: Se on määritelty etenemissuunta, jolla vektoritoiminto projisoidaan niin kauan kuin se on määritelty kyseiselle tasolle.

F: Vektorifunktio, jossa jokainen sen komponentti on määritelty funktiolla sellaisenaan (f, g).

V: Se on vektori tangentti R -alueelle, jolla integraali on määritelty. Tässä tapauksessa sitä käytetään tämän vektorin erotuksella.

Toisella termillä näemme Greenin kehittyneen lauseen, jossa havaitaan havaita. Alueiden erolle, joka ei ole muuta kuin molempien kahden dimensionaalisten erojen tuote (DX.dy).

Tätä lausetta sovelletaan täydellisesti avaruus- ja pinta -integraaleihin.

Esittely

Tämä tehtävä hajotetaan Greenin lauseen osoittamiseksi yksinkertaisella tavalla. Ensinnäkin oletamme, että vektori F -funktiolla on vain määritelmä versiossa Yllyttää. Kun taas versoria vastaava G -funktio J - on yhtä suuri kuin nolla.

Voi palvella sinua: kuinka monta sataa sopii kymmenesosaan? (Esimerkkejä)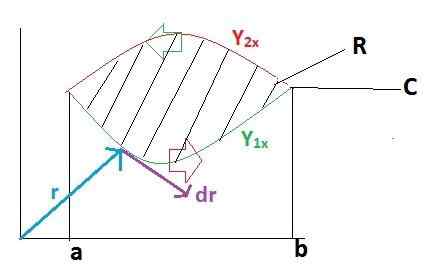Kirjoittaja

F = f (x, y)Yllyttää + G (x, y)J = f (x, y)Yllyttää + 0 -

R = xYllyttää + jaJ -

DR = DXYllyttää + DyJ -

Ensin kehitetään linja -integraali radalla C, jolle etenemissuunta on sektorisoitu kahdessa osassa, jotka menevät ensin A: sta B: hen ja B: n jälkeen A.

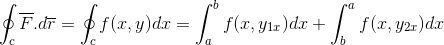
Määritetyn integraalin laskelman peruslauseen määritelmää sovelletaan.

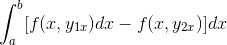
Express.

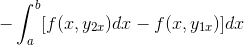
Tarkkailemalla yksityiskohtaisesti tätä lauseketta käy ilmi, että primitiivisen funktion kriteerejä sovellettaessa se on F: stä johdettu ekspression integraali suhteessa ja suhteessa suhteessa ja kohtaan. Arvioitu parametreina

[ja_1x , ja_2x-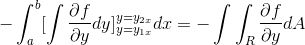

Nyt riittää olettamaan, että vektorihauskin funktio on määritelty vain g (x, y)J -. Jos toimitetaan edelliseen tapaukseen homologisoidulla tavalla, se saadaan:

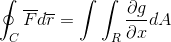
Lopuksi otetaan kaksi demonstrointia ja liittyvät tapaukseen, jossa vektoritoiminto ottaa arvot molemmille versioille. Tällä tavalla se näytetään linja -integraalina määrittelemisen jälkeen ja sitä pidetään yhden dimensionaalisena suuntauksena, se voidaan kehittää kokonaan tasolle ja tilalle.

F = f (x, y)Yllyttää + G (x, y)J -

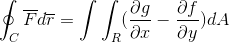
Tällä tavalla Greenin lause on osoitettu.

Sovellukset

Vihreiden lauseiden sovellukset ovat laajoja fysiikan ja matematiikan oksilla. Ne ulottuvat mihin tahansa sovellukseen tai käyttöön, jotka voidaan antaa linjan integrointiin.

Mekaaninen työ, jonka Force F on suorittanut radan C läpi.

Voi palvella sinua: Pentagonaalinen prisma: Ominaisuudet, osat, kärjet, reunat, tilavuus

Monien ulkoisten voimien altistuneiden elinten hitausmomentit eri sovelluspisteissä reagoivat myös kehitettäviin integraaleihin Greenin lauseen kanssa.

Tällä on useita toimintoja käytettävien materiaalien vastustutkimuksissa. Jos ulkoiset arvot voidaan määrittää ja ottaa huomioon ennen eri elementtien kehittämistä.

Yleensä Greenin lause helpottaa alueiden ymmärrystä ja määritelmää, joilla vektoritoiminnot määritellään alueen suhteen, radan mukaan.

Historia

Se julkaistiin vuonna 1828 teoksessa Matemaattinen analyysi sähkön ja magneettisuuden teorioille, Britannian matemaatikon George Greenin kirjoittama. Siinä tutkitaan melko ratkaisevia osia laskelman soveltamisessa fysiikassa, kuten potentiaalin käsite, vihreän toiminnot ja sen autolauseen sovellukset nimeltään.

George Green virallisti opiskelijauransa 40 -vuotiaana, toistaiseksi täysin itsetutkimuksen matemaatikko olemus. Opiskeltuaan Cambridgen yliopistossa hänen tutkimuksensa jatkuu, tekemällä panosta akustian, optiikan ja hydrodynamiikan alalla, jotka ovat edelleen voimassa.

Suhde muihin lauseisiin

Greenin lause on erityistapaus, ja se syntyy kahdesta muista erittäin tärkeistä lauseista laskentahaarassa. Nämä ovat Kelvin-Stokesin lause ja erimielisyys tai Gausski-lause.

Alkaen mistä tahansa molemmista lauseista voit saavuttaa Greenin lauseen. Tietyt määritelmät ja ehdotukset ovat välttämättömiä näiden mielenosoitusten kehittämiseksi.

Harjoitukset

- Seuraava harjoitus osoittaa, kuinka linja -integraali muuntaa kaksinkertaiseksi integraaliksi alueen R suhteen.

Alkuperäinen lauseke on seuraava:

Voi palvella sinua: kuinka paljon x arvoinen on?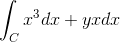

Ja on arvioitava kolmionmuotoisella alueella, joka liittyy pisteisiin (0, 0), (1, 0), (0, 1), jotka on merkitty C: llä. Tässä tapauksessa otetaan huomioon positiivinen käännöksen merkitys.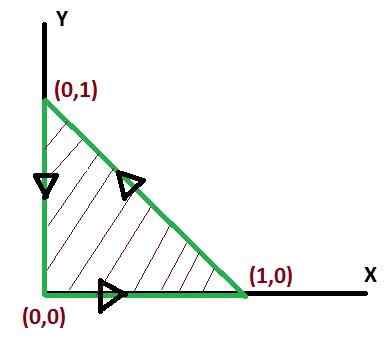

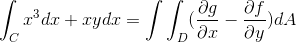
Missä F- ja G: tä vastaavat toiminnot otetaan

f (x, y) = x³                      g (x, y) = yx

df/dy = 0 dg/dx = y

On tärkeää määritellä toiminnot, jotka muodostavat alueen C rajat, jotta voidaan koota differentiaalituote, joka kattaa alueen kokonaan.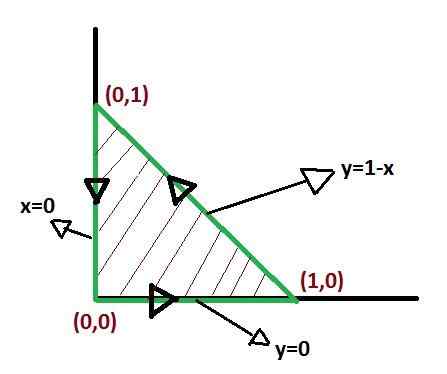

Greenin lausetta sovellettaessa ei ole ainutlaatuista tapaa määritellä integraatiorajoja. Mutta on muotoja, joissa integraalit määrittelemisen jälkeen voivat olla yksinkertaisempia. Siten, että integraatiorajojen optimointi ansaitsee huomion.

Tässä tapauksessa tätä ilmaisua otetaan huomioon: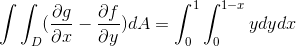

Missä saamme integraalit:

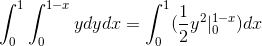
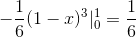
Tämä arvo vastaa kuutioyksiköitä vektorifunktion alapuolella olevalle alueelle ja C: n määrittelemällä kolmion muotoisella alueella.

Line -integraalin tapauksessa suorittamatta vihreää menetelmää, olisi ollut tarpeen parametroida toiminnot jokaisessa alueen osassa. Eli tee 3 parametroitua integraalia resoluutiolle. Tämä on riittävä näyttö tehokkuudesta, jonka Robert Green osallistui lauseeseensa laskelmaan.

Viitteet

1. Johdanto jatkumisen mekaniikkaan. W Michael Lai, David H. Rubin, Erhard Krempl, David Rubin Butterworth-Heinemann, 23. heinäkuuta. 2009
2. Monimuuttujainen laskenta. James Stewart. Cengage Learning, 22. maaliskuuta. 2011
3. Epävirallinen historia Greenin lauseesta ja niihin liittyvistä ideoista. James Joseph Cross. Matematiikan laitos, Melbournen yliopisto, 1975
4. Lämpökäyttäytyminen vihreiden toimintojen avulla. Kevin D. Cole, James V. Beck, a. Haji-Sheikh, Bahman Luckuhi. Taylor & Francis, 16. heinäkuuta. 2010
5. Greenin lauseen soveltaminen lineaaristen integraalien äärimmäisyyteen. Puolustustietokeskus, 1961