Lamyn lause

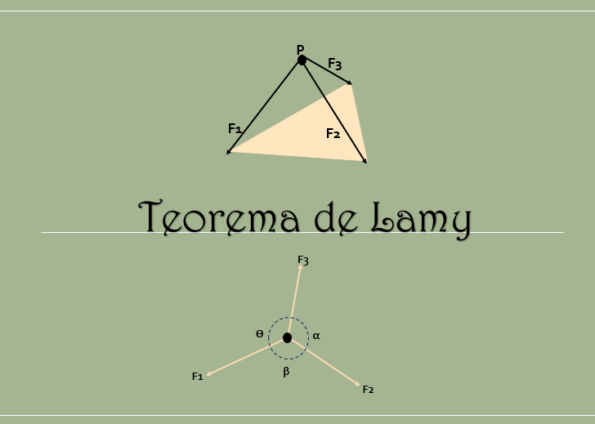
Lamyn lause osoittaa, että kun jäykkä ruumis on tasapainossa ja kolmen pariskierän (samassa tasossa) vaikutuksesta, niiden toimintalinjat ovat yhtä mieltä samassa vaiheessa.

Ranskan fyysikko ja uskonnollinen päätteli lauseen. Sitä käytetään laajasti kulman arvon, voiman toimintaviivan löytämiseen tai voimien kolmion muodostamiseen.

Selitys

Lause toteaa, että tasapainon ehdon toteuttamiseksi voimien on oltava koplaaneja; toisin sanoen pisteeseen kohdistettujen voimien summa on nolla.

Lisäksi, kuten seuraavassa kuvassa nähdään, on täytettävä, että jatkamalla näiden kolmen voiman toimintalinjoja, ne ovat samaa mieltä samassa vaiheessa.

Siten, jos kolme voimaa, jotka ovat samassa tasossa ja samanaikaisesti, kunkin voiman suuruus on verrannollinen vastakkaisen kulman rintaan.

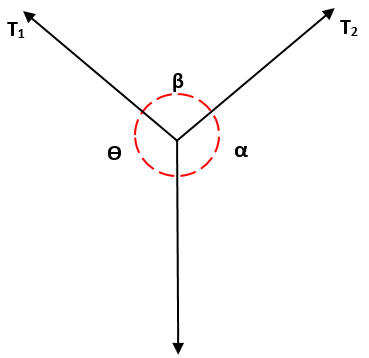
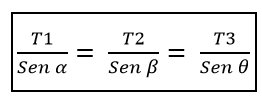
Tämän on oltava T1, alkaen α: n rinnasta, se on yhtä suuri kuin T2 / β: n suhde, joka puolestaan ​​on yhtä suuri kuin T3 / ɵ: n suhde, ts.:

Sieltä seuraa, että näiden kolmen voiman moduulien on oltava samat, jos kunkin voiman parin muodostavat kulmat ovat yhtä suuret kuin 120º.

On mahdollista, että yksi kulmista on tylsä ​​(mittaa välillä 90^{0 -} ja 180^{0 -}-A. Tällöin kyseisen kulman rinta on yhtä suuri kuin lisäkulman rinta (parissa se mittaa 180^{0 -}-A.

Liikuntaa

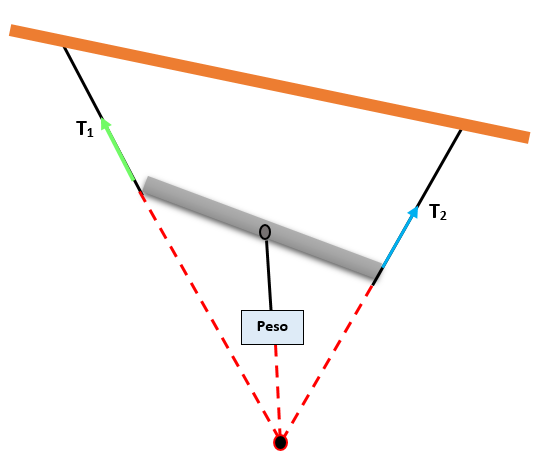
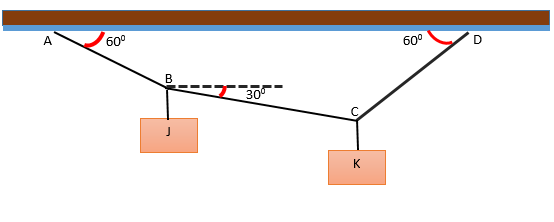
Kahden J- ja K -lohkon muodostama järjestelmä, joka roikkuu useissa kielissä, jotka muodostavat kulmia vaakatasossa, kuten kuvassa on esitetty. Järjestelmä on tasapainossa ja J -lohko painaa 240 N. Määritä lohkon K paino.

Ratkaisu

Vaikutus- ja reaktioperiaatteella lohkoihin 1 ja 2 kohdistuvat jännitteet ovat yhtä suuret kuin näiden paino.

Nyt jokaiselle lohkolle on rakennettu vapaa kehon kaavio ja määritä siten järjestelmän muodostavat kulmat.

On tiedossa, että köyden, joka menee A - B, kulma on 30^{0 -} , niin, että se täydentää kulma on yhtä suuri kuin 60^{0 -} . Tällä tavalla saavut 90^{0 -}.

Toisaalta, missä piste A sijaitsee, on 60 kulma^{0 -} Vaakasuoran suhteen; Pystysuoran ja t välinen kulma_-Lla Se on = 180^{0 -} - 60 60^{0 -} - 90^{0 -} = 30^{0 -}.

Siten saadaan, että AB: n ja BC = välinen kulma (30^{0 -} + 90^{0 -} + 30^{0 -}) ja (60^{0 -} + 90^{0 -} + 60) = 150^{0 -} ja 210^{0 -}. Liittyessään on varmistettu, että kokonaiskulma on 360^{0 -}.

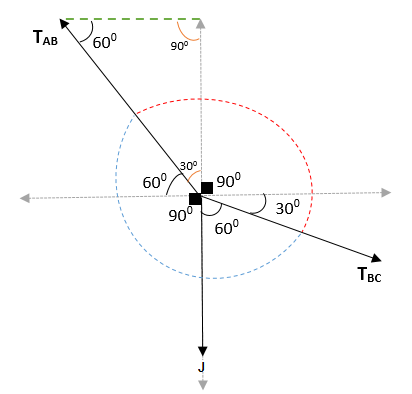
Lamyn lauseen soveltaminen:

T_BC/ Sin 150^{0 -} = P_-Lla/ Sin 150^{0 -}

T_BC = P_-Lla

T_BC = 240N.

Kohdassa C, missä lohko on, vaakasuoran ja BC -köyden välinen kulma on 30 on 30^{0 -}, Joten täydentävä kulma on yhtä suuri kuin 60^{0 -}.

Toisaalta kulma on 60^{0 -} CD -pisteessä; Pystysuoran ja t välinen kulma_C Se on = 180^{0 -} - 90^{0 -} - 60 60^{0 -} = 30^{0 -}.

Siten saadaan, että lohkon K kulma on = (30^{0 -} + 60 60^{0 -}-A

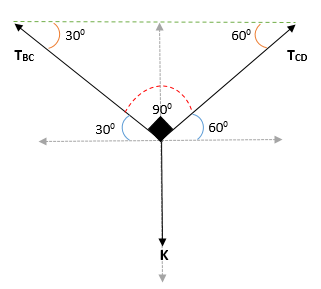
Lamyn lauseen soveltaminen kohtaan C:

T_BC/ Sin 150^{0 -} = B / sin 90^{0 -}

Q = t_{BC *} Sen 90^{0 -} / Sin 150^{0 -}

Q = 240 N * 1/0,5

Q = 480 N.

Viitteet

1. Ferdinand p. Olut, e. R -. (2013). Insinöörien mekaniikka, staattinen. McGraw-Hill-Amerikanvälinen.
2. Francisco Español, J. C. (2015). Ratkaistu lineaarinen algebra -ongelmat. Paraninfo Editions, S.-Lla.
3. Graham, J. (2005). Vahvuus ja liike. Houchton Mifflin Harcourt.
4. Harpe, P. d -d. (2000). Geometrisen ryhmäteorian aiheet. University of Chicago Press.
5. P. A tpler y, g. M. (2005). Fysiikka tieteen ja tekniikan puolesta. Osa. Barcelona: Palauta sinut.-Lla.