Thévenin -lause, mikä koostuu, sovelluksia ja esimerkkejä

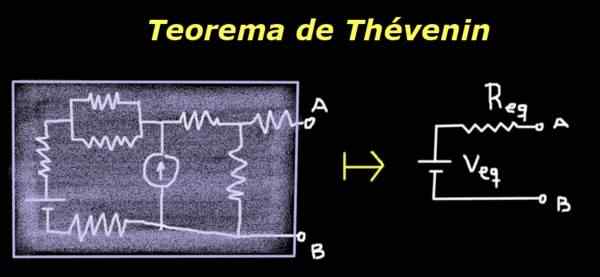
Hän Thévenin -lause Siinä todetaan, että piiri A ja B: n piiri voidaan korvata vastaavalla ekvivalentilla, joka koostuu lähteestä ja sarjankestävyydestä, joiden arvot antavat saman potentiaalieron A: n ja B: n ja saman impedanssin välillä kuin alkuperäinen piiri.

Ranskalainen insinööri Léon Charles Thévenin vapautti tämän lauseen vuonna 1883, mutta väitetään, että saksalainen fyysikko Hermann von Helmholtz väitti, että hänet totesi kolmekymmentä vuotta ennen.

Kuvio 1. Thévenin -lause. Lähde: Itse tehty

Sen hyödyllisyys on siinä tosiasiassa, että vaikka alkuperäinen piiri olisi monimutkainen tai tuntematon, kuorman tai impedanssin tarkoituksiin, jotka asetetaan terminaalien A ja B väliin, théveninin yksinkertainen vastaava piiri käyttäytyy samalla tavalla kuin alkuperäinen.

[TOC]

Kuinka vastaava jännite askel askeleelta lasketaan?

Vastaavan piirin jännite tai potentiaaliero voidaan saada seuraavilla tavoilla:

- Kokeellisesti

Théveninin vastaavan jännitteen saaminen

Jos se on laite tai laite, joka on ”mustassa laatikossa”, potentiaaliero a ja b väliset volttimittarit tai oskilloskooppi mitataan. On erittäin tärkeää, ettei napa A: n ja B välillä ole kuormitusta tai impedanssia. 

Volattimittari tai oskilloskooppi ei edusta mitään kuormaa päätelaitteille, koska molemmilla joukkueilla on erittäin suuri (ihanteellisesti ääretön) impedanssi ja ne olisivat ikään kuin terminaalit A ja B olisivat ilman kuormaa. Tällä tavalla saatu jännite tai jännite on Théveninin vastaava jännitys.

Théveninin vastaavan impedanssin saaminen

Vastaavan impedanssin saamiseksi kokeellisesta mittauksesta asetetaan A- ja B -päätteiden välillä tunnettu vastus ja jännitepisara tai jännitesignaali oskilloskoopilla mitataan. 

Pitterminaalien keskuudessa tunnetun vastusjännitteen pudotuksesta sen läpi kiertävä virta voidaan saada. 

Virran tuote, joka on saatu vastaavalla vastustuskestävyydellä plus tunnettujen vastustuskyvyn mitattu jännitepisara on yhtä suuri kuin aikaisemmin saadun Théveninin vastaava jännite. Tästä tasa -arvosta Théveninin vastaava impedanssi puhdistetaan.

- Piirin ratkaiseminen

Théveninin vastaava jännitteen laskenta

Ensinnäkin, mikä tahansa päätelaitteiden A ja B kuormitus tai impedanssi on irrotettu.

Kuten piiri tiedetään, silmät tai Kirchhoffin lakeja sovelletaan levojen löytämiseen terminaaleissa. Tämä jännitys on Théveninin vastaava.

Voi palvella sinua: Mount Olympus (Mars)

Théveninin vastaava impedanssilaskelma

Vastaavan impedanssin saamiseksi jatkamme:

- Vaihda alkuperäiset piirin jännitelähteet lyhyillä alueilla "nollaimpedanssi" ja alkuperäisen piirin lähteet avoimelle "äärettömälle impedanssille".

- Sitten vastaava impedanssi lasketaan sarjan impedanssin ja impedanssien sääntöjen mukaisesti rinnakkain.

Thévenin -lauseen sovellukset (osa I)

Käytämme Théveninin lauseita ratkaistaksesi joitain piirejä. Tässä ensimmäisessä osassa tarkastellaan piiriä, jolla on vain jännityslähteet ja resistanssit.

Esimerkki 1 (vastaavan jännitteen laskenta vaihe vaiheelta)

Kuvio 2 esittää piirin, joka on taivaallisessa laatikossa, jossa on kaksi akkua elektromotorista Force V1: tä ja V2: ta, ja resistanssit R1 ja R2, piirissä on liittimet A ja B, joihin kuorma voidaan kytkeä.

Kuva 2. Esimerkki 1 Thévenin -lauseesta. Lähde: Itse tehty

Tavoitteena on löytää vastaava piiri, ts. Määritä vastaavan piirin VT- ja RT -arvot.  Käytä seuraavia arvoja: V1 = 4V, V2 = 1 V, R1 = 3Ω, R2 = 6Ω ja R = 1Ω.

Askel askeleelta

Vaihe 1 

Määritämme liittimien A ja B jännitteen, kun niille ei ole mitään kuormaa.

Vaihe 2

Ratkaiseva piiri koostuu yhdestä verkkosta, jonka läpi virran, jonka kiertää, että olemme ottaneet positiivisesti myötäpäivään.

Vaihe 3

Matkamme verkkoa alkaen vasemmasta alakulmasta. Reitti johtaa seuraavaan yhtälöön:

V1 - i*r1 - i*r2 - v2 = 0

Vaihe 4

Tyhjennämme verkkovirran I ja saamme:

I = (V1 -V2) / (R1 +R2) = (4V - 1 V) / (3Ω +6Ω) = ⅓ A

Vaihe 5

Mesh -virran avulla voimme määrittää A: n ja B: n välisen jännitteen tai jännitteen eron, mikä on:

VAB = V1 - i * R1 = 4V - ⅓ A * 3Ω = 3V

Toisin sanoen Theveninin vastaava jännite on: VT = 3V.

Vaihe 6 (Théveninin vastaava vastus))

Jatkamme nyt Théveninin vastaavan resistanssin, jolle ja kuten aiemmin sanottiin, jännitelähteet korvataan kaapelilla.

Tällöin meillä on vain kaksi vastustuskykyä rinnakkain, joten Théveninin vastaava vastus on:

RT = (R1 * R2) / (R1 + R2) = (3Ω * 6Ω) / (3ω + 6Ω) = 2Ω

Esimerkki 1B (virtavirta käyttämällä Thévenin -ekvivalenttia)

Yhdistä kuormana napoihin A ja B A Vastaus r = 1Ω vastaavaan piiriin ja löydä virran, joka kiertää mainittua kuormaa. 

Voi palvella sinua: Strektiliininen liike: Ominaisuudet, tyypit ja esimerkit

Ratkaisu

Kun vastus r on kytketty Theveninin vastaavaan piiriin, on yksinkertainen piiri, joka koostuu VT -lähteestä A -sarjan vastus sarjassa vastus r. 

Kutsumme virran, joka kiertää kuorman R läpi, niin että verkkoyhtälö on tällainen:

Vt - ic* rt - ic* r = 0

Josta seuraa, että IC: n annetaan:

Ic = vt / (rt + r) = 3v / (2Ω + 1Ω) = 1 a

Thévenin -lauseen varmennus

Yhdistä r alkuperäiseen piiriin varmistaaksesi, että Théveninin lause on täytetty, ja löydä virran, joka kiertää R: n soveltamalla silmänlaki tuloksena olevaan piiriin.

Tuloksena oleva piiri pysyy ja sen verkkoyhtälöt ovat seuraavassa kuvassa esitetty:

Kuva 3. Verkkovirrat. (Oma yksityiskohta)

Mesh -yhtälöiden lisääminen on mahdollista löytää verkkovirta i1 virrasta I2 riippuen. Sitten se korvataan toisessa mesh -yhtälössä ja I2: n kanssa on yhtälö ainoana tuntemattomana. Seuraava taulukko näyttää toiminnot.

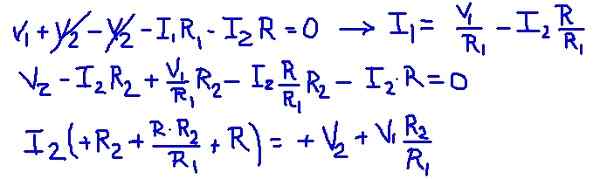Kuva 4. Yksityiskohta toiminnoista. (Oma yksityiskohta)

Sitten korvataan lähteiden vastusarvot ja jännitteet, jotka saavat i2 -mesh -virran numeerisen arvon.

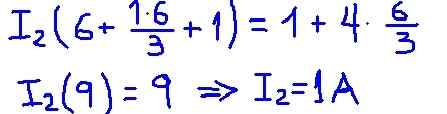Kuva 5. Tulos yksityiskohdat. (Oma yksityiskohta)

I2 -mesh -virta on virta, joka kiertää kuormitusvastuksen R läpi ja 1: stä löydetty arvo on täysin samaan aikaan kuin aiemmin löydettiin vastaavan Théveninin vastaavan piirin kanssa.

Théveninin lauseen (osa II) soveltaminen

Tässä toisessa osassa Théveninin lause sovelletaan piiriin, jolla on jännityslähteet, virran lähde ja vastus. 

Esimerkki 2A (Théveninin vastaava vastus))

Tavoitteena on määrittää seuraavan kuvan piiriä vastaavan théveniinin vastaava piiri, kun napit ovat ilman 1 ohmion vastustusta, niin vastus asetetaan ja virran virta määritetään samalla tavalla.

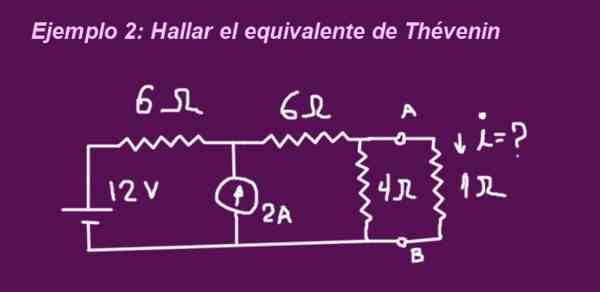Kuva 6. Esimerkki 2 piiri. (Oma yksityiskohta)

Ratkaisu

Vastaavan vastuskyvyn löytämiseksi kuormitusvastus poistetaan (tässä tapauksessa 1 ohmion vastus). Lisäksi jännitelähteet korvataan oikosulkulla ja virranlähteillä avoimella piirillä. 

Tällä tavalla piiri, johon vastaava vastus lasketaan, on alla esitetty:

Voi palvella sinua: Boltzmann vakio: historia, yhtälöt, laskelmat, harjoitukset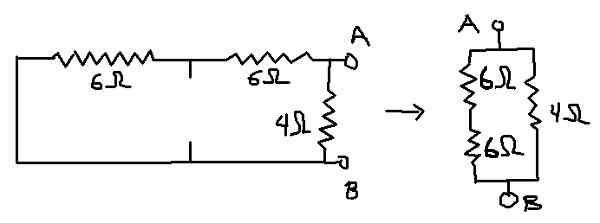Kuva 7. Yksityiskohta ekvivalenttivastuksen laskemiseksi (oma yksityiskohta)

Rab = (12Ω * 4Ω) / (12Ω + 4Ω) = 3Ω, joka on Theveninin (rth) vastaava vastus (rth).

Esimerkki 2b 

Laske Théveninin vastaava jännite.

Ratkaisu

Théveninin vastaavan jännitteen laskemiseksi tarkastellaan seuraavaa piiriä, johon sijoitetaan virrat I1: een ja I2: een seuraavaan kuvaan ilmoitettuihin oksille:

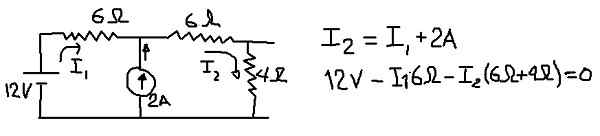Kuva 8. Yksityiskohdat Théveninin jännityksen laskemisesta. (Oma yksityiskohta)

Edellisessä kuvassa nykyisten solmujen yhtälö ja jännitteen yhtälö esitetään, kun ulkoista verkkoa kuljetetaan. Toisesta yhtälöistä nykyinen i1 puhdistetaan:

I1 = 2 - i2*(5/3)

Tämä yhtälö korvataan solmujen yhtälössä:

I2 = 2 - (5/3) i2 + 2 ===> i2 (8/3) = 4 ===> i2 = 12/8 = 1,5 a

Tämä tarkoittaa, että jännitteen pudotus 4 ohmin vastus on 6 volttia.

Lyhyesti sanottuna Théveninin jännitys on v. = 6 V.

Esimerkki 2C

Etsi Theveninin ja virran vastaava piiri kuormituksen vastustuskykyä.

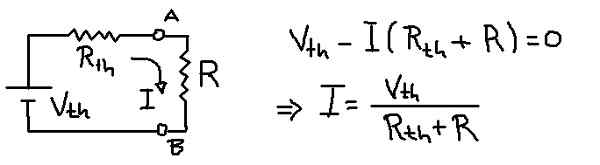Kuva 9. Virta kuormituksessa Théveninin vastaavalla. (Oma yksityiskohta)

Ratkaisu

Edellinen kuva näyttää théveninin vastaavan piirin kuormitusvastuksella r. Meshin jänniteyhtälöstä virran i, joka kiertää kuormankestävyyden R läpi, johdetaan.

I = vth / (rth + r) = 6v / (3ω + 1Ω) = 1,5 a

Théveninin lauseen soveltaminen (osa III)

Tässä kolmannessa Théveninin lausekeskuksessa vuorotteleva virtapiiri sisältää vuorottelevan jännitteen lähteen, lauhduttimen, induktanssin ja vastustuskyvyn otetaan huomioon. 

Esimerkki 3

Tavoitteena on löytää seuraavan piirin vastaava Thévenin -piiri:

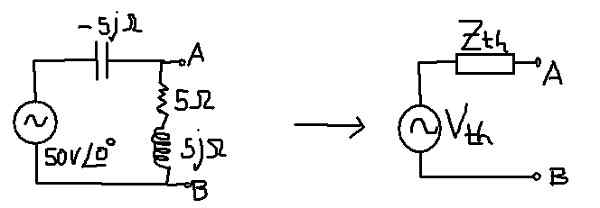Kuva 10. Thévenin vuorotellen virtapiirissä. (Oma yksityiskohta)

Ratkaisu

Vastaava impedanssi vastaa lauhduttimen vastustuskykyä rinnakkain vastus- ja induktanssisarjan yhdistelmän kanssa.

Vastaavan impedanssin käänteinen annetaan:

Zeq^-1 = (-5j)^-1 + (5 + 5J)^-1 = (1/5) J + ((1/10 + (1/10) j) = (1/10 + 3/ 10 j) mho

Ja vastaava impedanssi on sitten:

Zeq = (1 - 3 J) ohm

Kompleksi virra, jonka voin päätellä verkkoyhtälöstä:

50V>0 - I (-5 J + 5 + 5J) = 50 V> I*5 = 0 ===> I = 10a ∠0 

Nyt lasketaan jänniteprosentti ja induktanssi, ts. VAB -jännitys, joka on Théveninin vastaava jännitys:

VAB = I * (5 + 5 J) ω = 10A ∠0 * 5Ωlla45º = 50 V kerran45º

Toisin sanoen

Viitteet

1. Elektroniikkaoppaat, Theveninin lause. Toipunut: Elektroniikka-Tormales.WS
2. Verkkoteorian kysymykset ja vastaukset. Theveninin lause. Toipunut: Sanfoundry.com
3. Theveninin lause. Askel askeleelta. Toipunut: sähköteknologia.org
4. Theveninin lause. Ratkaistu esimerkki askel askeleelta. Haettu: ElecticalSimple.Blogin.com
5. Työpaja Theveninin ja Nortonin lauseissa. Haettu: Web.iit.Edu
6. Wikipedia. Thévenin -lause. Toipunut: Wikipedia.com