Varsignonilause

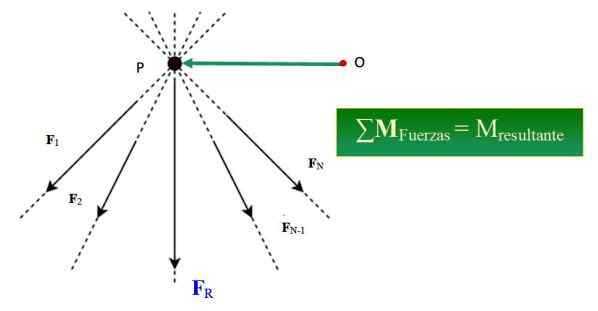
Kuvio 1.- Varignonin lause vakuuttaa, että tietyn pisteen ympärillä olevien voimien hetken summa vastaa tulosaikaa kyseisen pisteen suhteen. Lähde: Wikimedia Commons/F. Zapata.

Mikä on Varignonin lause?

Varsignonin lause mekaniikassa todetaan.

Tästä syystä tämä lause tunnetaan myös nimellä Hetkien alku.

Vaikka ensimmäinen ilmoitti, että hollantilainen Simon Stevin (1548-1620), hydrostaattisen paradoksin luoja, ranskalainen matemaatikko Pierre Varignon (1654-1722) oli se, joka myöhemmin antoi hänelle lopullisen muodonsa.

Esimerkki siitä, kuinka Varignonin lause toimii mekaniikassa F₁ ja F₂, (Merkitty lihavoidulla vektorihahmoonsa). Nämä voimat aiheuttavat netto- tai tuloksena olevan voiman, jota kutsutaan F_{R -}.

Jokainen voima käyttää vääntömomenttia tai hetken pisteeseen tai, joka on laskettu vektorituotteella sijaintivektorin välillä r -_Oppi Ja rasitus F, missä r -_Oppi Se on suunnattu samanaikaisesti tai siihen pisteeseen p:

M_O1 = r -_Oppi × F₁

M_O2 = r -_Oppi × F₂

Kun otetaan huomioon F_{R -} = F₁ + F₂, niin:

M_JOMPIKUMPI = r -_Oppi × F₁ + r -_Oppi × F₂ = M_O1 + M_O2

Mutta miten r -_Oppi Se on sitten yleinen tekijä jakautuvan ominaisuuden soveltaminen ristiintuotteeseen:

M_JOMPIKUMPI = r -_Oppi × (F₁ + F₂) = r -_Oppi × F_{R -}                

Siksi kunkin voiman hetkien tai vääntömomenttien summa pisteeseen nähden tai vastaa tuloksena olevan voiman ajankohtana samaan kohtaan.

Lausunto ja esittely

Olla N: n samanaikaisten voimien järjestelmä, jonka on muodostettu F₁, F₂, F₃.. F_N, jonka toimintalinjat on tarkoitettu kohtaan P (katso kuva 1), tämän voiman järjestelmän hetki M_JOMPIKUMPI, Kohdan tai sen annetaan:

Voi palvella sinua: Epävakaa tasapaino: Konsepti ja esimerkit

M_JOMPIKUMPI = r -_Oppi × F₁ + r -_Oppi × F₂ + r -_Oppi × F₃ +.. r -_Oppi × F_N = r -_Oppi × (F₁ + F₂ + F₃ +.. F_N-A

Esittely

Lauseen osoittamiseksi tehdään vektorituotteen jakautuva ominaisuus vektorien välillä.

Olla voimassa F₁, F₂, F₃.. F_N kohdistaa jhk₁, -Lla₂, -Lla₃…_N ja samanaikainen kohdassa P. Tämän järjestelmän tuloksena oleva hetki suhteessa pisteeseen tai nimeltään M_JOMPIKUMPI, Se on kunkin voiman hetkien summa siihen kohtaan:

M_JOMPIKUMPI = ∑ r -_OAI × F_Yllyttää

Missä summa menee välillä i = 1 - i = n, koska n -voimia on. Koska nämä ovat samanaikaisia ​​voimia ja koska vektorituote rinnakkaisvektoreiden välillä on nolla, tapahtuu, että:

r -_Pai × F_Yllyttää = 0 -

Nollavektorilla merkittynä 0 -.

Yhden O: n voiman, esimerkiksi voiman hetken hetki F_Yllyttää sovellettu a_Yllyttää, Se on kirjoitettu näin:

M_kuulin = r -_OAI × F_Yllyttää

Sijaintivektori r -_OAI  Se voidaan ilmaista kahden vektorin sijainnin summana:

r -_OAI = r -_Oppi + r -_Pai

Tällä tavalla hetki suhteessa tai pakottamiseen F_Yllyttää On:

M_kuulin = (r -_Oppi + r -_Pai) × F_Yllyttää = (r -_Oppi × F_Yllyttää) + (r -_Pai × F_Yllyttää-A

Mutta viimeinen termi on tyhjä, kuten edellä selitetään, koska r -_Pai on toimintalinjalla F_Yllyttää, siksi:

M_kuulin = r -_Oppi × F_Yllyttää

Tietäen, että järjestelmän hetki pisteeseen tai on kunkin voiman kaikkien yksittäisten hetkien summa siihen kohtaan, sitten:

M_JOMPIKUMPI = ∑ M_kuulin = ∑ r -_Oppi × F_Yllyttää

Kuten r -_Oppi Se on jatkuvaa, summasta:

M_JOMPIKUMPI = r -_Oppi × (∑ F_Yllyttää-A

Mutta ∑ F_Yllyttää Se on yksinkertaisesti tuloksena oleva verkko tai voima F_{R -}, Siksi heti päätellään, että:

Voi palvella sinua: Leyden -pullo: Osat, toiminta, kokeet

M_JOMPIKUMPI = r -_Oppi × F_{R -}

Esimerkki

Varsignonin lause helpottaa voiman hetken laskemista F Kuvassa esitetyn pisteen tai rakenteen suhteen, jos voima jaotellaan suorakulmaisiin komponentteihin ja niiden momentti lasketaan:

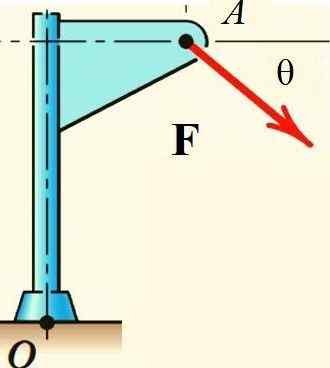Kuva 2.- Varsignonin lause sovelletaan laskemaan voimanmomentti tai. Lähde: f. Zapata.

Varsignon -lauseen sovellukset

Kun järjestelmästä saatu voima tiedetään, Varignonin lause voidaan käyttää korvaamaan kunkin voimien tuottamien momenttien summa, jotka säveltävät sen tuloksen aikaan.

Jos järjestelmä koostuu samassa tasossa olevista voimista ja siitä, että suhteessa haluat laskea hetken kuuluu siihen tasoon, tuloksena oleva hetki on kohtisuorassa.

Esimerkiksi, jos kaikki voimat ovat XY -tasossa, hetki on suunnattu Z -akselille ja jäljellä vain sen suuruuden ja merkityksen löytämiseksi, kuten edellä kuvatun esimerkin tapauksessa.

Tällöin Varignonin lause mahdollistaa järjestelmästä johtuvan momentin laskemisen summauksen kautta. Se on erittäin hyödyllinen kolmen ulottuvuuden voiman järjestelmän tapauksessa, jolle tuloksena olevan hetken suunnasta ei tunneta etukäteen.

Näiden harjoitusten ratkaisemiseksi se on kätevä.

Liikuntaa

Laske Varignonin lauseen avulla F voiman F -momentti pisteen ympärillä tai esitetty kuvassa, jos F on 725 N.

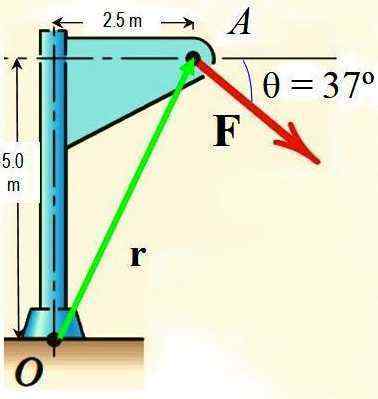Kuva 3.- Harjoituksen luku ratkaistu. Lähde: f. Zapata.

Ratkaisu

Sovelletaan Varsignonin lause, Force hajoaa F kahdessa komponentissa, joiden vastaavat hetket ympärillä tai lasketaan ja lisätään saadaan hetken saamiseksi.

Voi palvella sinua: jäykkä ruumis

F_x = 725 n ∙ cos 37 º = 579.0 N

F_ja = - 725 n n ∙ Sen 37 º = −436.3 n

Samoin sijaintivektori r - Ohjatulla tai A: lla on komponentit:

r -_x = 2.5m

r -_ja = 5.0 m

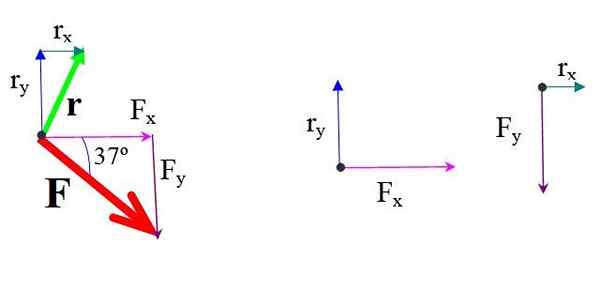Kuva 4.- Voima- ja sijaintikomponentit. Lähde: f. Zapata.

Voiman kunkin komponentin momentti suhteessa voimaan ja kohtisuoraan etäisyyteen.

Molemmilla voimilla on taipumus kiertää rakennetta samaan suuntaan, mikä tässä tapauksessa on pistemäärä, jolle on annettu mielivaltaisesti positiivinen merkki:

M_Härkä = F_x∙ r_ja ∙ Sin 90º = 579.0 N ∙ 5.0 m = 2895 n ∙ m

M_Oy = F_ja∙ r_x ∙ synti (−90º) = −436.3 n ∙ 2.5 m ∙ (−1) = 1090.8 n ∙ m

Tuloksena oleva hetki suhteessa tai on:

M_JOMPIKUMPI = M_Härkä + M_Oy = 3985.8 n ∙ m kohtisuorassa tasoon ja vääntömomenttiin.

Viitteet

1. Bedford, 2000. -Lla. Tekniikan mekaniikka: staattinen. Addison Wesley. 
2. Olut, f. 2010. Staattinen. McGraw Hill. 9NA. Painos.
3. Hibbeler, R. 1992. Insinöörien mekaniikka. Kuudes. Painos. CECSA.
4. HK -tekniikka. Varsignonilause. Palautettu: YouTube.com.
5. Wikipedia. Varsignonin lause (mekaniikka). Haettu: vuonna.Wikipedia.org.