Tetradecágono

Mikä on tetradecágono?

Tetradecágono on litteä ja suljettu geometrinen kuva 14 sivua, jotka kuuluvat Polygons -perheelle. Se tunnetaan myös nimellä tetrakaidecágono, Kaikki kreikkalaisista sanoista johdetut sanat: "Tetra" (cuatri), "Kai" (lisää), "rappeutuminen" (kymmenen) ja "gon" (kulma), koska siinä on myös 14 sisäkulmaa.

Kuvassa on säännöllinen tetradagon, ts. Yksi, jonka sivuilla ja sisäkulmilla on sama mitta, joka näyttää tämän luvun pääominaisuudet.

Kuvio 1.- Säännöllinen tetrade pääominaisuuksillaan. Lähde: f. Zapata.

Tetradecágono -elementit

• Puolet: Niitä kutsutaan 14 linjasegmentiksi, jotka on suljettu kuvan muodostamiseksi. Heillä kaikilla voi olla samanpituus, jolloin monikulmio on säännöllinen tai ne voivat olla erilaisia ​​ja sitten on epäsäännöllinen tetrade.
• Kärjet: Ne ovat risteyspisteitä peräkkäisten segmenttien ja tetradecágonon välillä 14 kärkeä.
• Keskusta: Paritsin tasa -arvoinen kohta.
• Radio: segmentti, joka yhdistää keskuksen kärkipisteellä.
• Sisäkulma: Se muodostuu kuvan sisäpuolelta ja kahden peräkkäisen tai viereisen segmentin välillä. Mitat 154.286º tavalliselle tetradecágonille, sivun koosta riippumatta.
• Ulkokulma: muodostettu yhden sivun ja yhden viereisen puolen pidentymisen väliin. Sivupituudesta riippumatta, tämä kulma mittaa 25.7143º tavalliselle tetradelle.
• Keskikulma: Se, jonka kärkipiste on samanaikainen monikulmion keskustan ja sen sivujen kanssa, on kaksi peräkkäistä radiota.
• Diagonaali: segmentti, joka yhdistää kaksi ei -säilytyskäsitystä.

Kuinka tetradecágono on?

Säännöllä ja kompassilla rakennetuilla N -puolilla olevilla N -puolilla on muodoltaan 2 N^{r -} p₁… P_{k -k -}, P -oleminen_Yllyttää Fermat Primo numerot erilaiset, ja puolestaan ​​Fermatin alusluvut muodostuvat 2ⁿ + 1.

Voi palvella sinua: Rivin odottaminen: Kaava ja yhtälöt, esitys, esimerkit

Tetradecágonolla on n = 14 puolta, mutta 14 = 7 × 2, jotka eivät ole Fermat -serkkuja, koska niitä ei voida ilmaista ilmoitetulla tavalla. Siksi tämä monikulmio ei myönnä tarkkaa rakennetta sääntöllä ja kompassilla, vaan rakenne, joka lähestyy erittäin hyvin useiden menetelmien avulla.

Yleinen menetelmä tavallisten monikulmioiden rakentamiseksi

Seuraava on yleinen menetelmä (ei ainoa), joka rakentaa säännöllisiä monikulmioita, jotka on rekisteröity kehälle, mukaan lukien tavallinen tetrade.

Se koostuu tämän kehän pystysuuntaisen halkaisijan jakamisesta yhtä moniin yhtä suuriin osiin kuin sivuilla on monikulmio piirtää. Tetradecágonon tapauksessa ne ovat 14 osassa, jotka on numeroitu kuvassa 2. Nämä ovat vaiheet:

• Piirrä pystysuora halkaisija A: sta B: hen.
• Piirrä sitten puoliksi oikeasta pisteestä A alkaen, avaa kompassi mielivaltaisella aukkolla ja tee siitä 14 tasaisesti etäisyydellä sijaitsevaa jakoa. Semirrect ja sen jakautumiset voivat päästä pois kehästä.
• Liity 14Va -tuotemerkkiin (kuvassa sininen) puoliksi oikean pisteen B lopussa.
• Jatkamaan liittymistä muihin puoliaineen merkinnöihin pystysuoran halkaisijan vastaavien pisteiden kanssa (vihreät pisteet).
• Kompassin kärjessä a ja aukko, joka on yhtä suuri kuin ympärysmitta, kaari vedetään. Samalla mittauksella, mutta tukee kärkeä B: ssä (kuvion 2 piste 14).

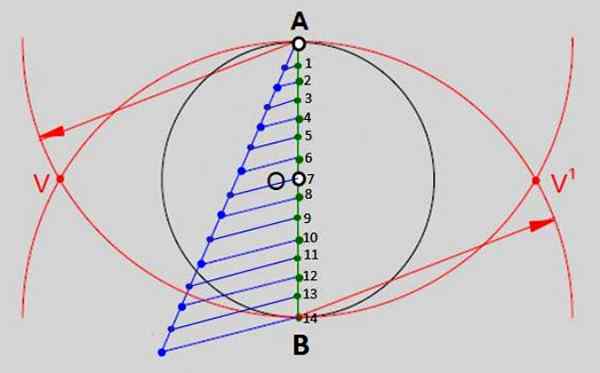Kuva 2.- Yksi yleisistä menetelmistä tavallisten monikulmioiden rakentamiseksi on jakaa kehän halkaisija niin moniin yhtä suuriin osiin kuin puolilla on monikulmio. Tavallisen tetradechin tapauksessa on 14 yhtä suurta osaa. Lähde: f. Zapata.

• Piirrä nyt sääntöllä viiva v ': stä pisteeseen 2 ja pidentämään sitä leikkaamaan ympärysmitta kuvion 3 kohdassa C. Merkitse leikkauspiste, joka on yksi kuvan kärkipisteistä.

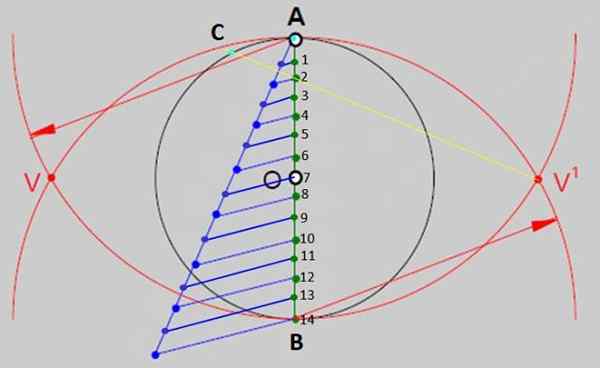Voi palvella sinua: Tilasto -oksat Kuva 3.- AC -segmentti on rakennetun tetradecionin sivujen mittaus. Lähde: f. Zapata.

• Avaa kompassi vaihtovirta -etäisyydellä ja tue kärkeä A tai C: ssä, piirtäen yhtä suuret mittaiset kaarit koko kehän yli, tällä tavalla se on jaettu suunnilleen yhtä suuriksi osiin, kaarien ja kehän väliset risteykset ovat kärkipisteitä Tetradecágonon huiput.
• Liity sääntöllä kärkipisteisiin linjasegmenteillä muodostaen monikulmion sivut.
• Poistaa varovasti apurakenteet.

Seuraavassa animaatiossa esitetään toinen likimääräinen menetelmä, sääntöllä ja kompassilla:

Kuva 4.- Animaatio, joka osoittaa, kuinka tetradecágon tehdään (suunnilleen tavallinen monikulmio). Lähde: Wikimedia Commons.

Kaavat tavalliselle tetradelle

Seuraavat kaavat ovat voimassa tavallisille monikulmoille:

• Arkin numero: n
• Sivumitta: a
• Apoteemi: l_-Lla
• Radio: r
• Kehä: P
• Alue: a
• Sisäinen kulma: I
• Ulkoinen kulma: e
• Diagonaali: D

Tunnettu puoli Apothem

A = 2L_-Lla × TG (π/N)

N = 14:

A = 2L_-Lla × TG (π/14)

Tunnetun puolen radio

A = 2R × Sen (π/N)

Kyllä n = 14:

A = 2R × Sen (π/14)

Tunnettu kehä sivu

Kehä on sivujen summa. Kun tetradecágono on säännöllinen:

P = n⋅a = 14⋅a

Jos tetradecágono on epäsäännöllinen, kaikki sivut on lisättävä suoraan kehän saamiseksi.

Tunnettu alue sivu

A = ¼ NA² × pinnasänky (π/n)

N = 14:

A = ¼ (14²) × pinnasänky (π/14) = (7/2) a² × pinnasänky (π/14)

Tunnettu alue

A = n⋅l_-Lla ² × TG (π/N)

N = 14 tulosta:

A = 14L_-Lla ² × TG (π/14)

Alue perustuu kehään ja apoteemiin

A = (P × L_-Lla)/2

Voi palvella sinua: Bayes -lause

Sisäkulmamitta

 Kun n = 14, tetradecágonon sisäkulma mittaa asteina:

I = 12 × 180º /14 = 154.286º

Ulkoisen kulman mittaus

E = 360º/N

Kun n = 14 sinulla on:

E = 25.7143º

Diagonaalit

Kaava missä tahansa monikulmiossa olevien diagonaalien lukumäärän laskemiseksi, säännöllisesti tai ei, on:

N = 14:

D = 14 × 11/2 = 77 diagonaalia

Esimerkit

Toinen esimerkki Tetradecágonista

Säännölliset monikulmiot ilmestyvät toistuvasti lukuisissa malleissa, kuten valuutoissa. Säännöllisen tetradagonin tapauksessa tämä esiintyy malesialaisissa muistokolikoissa, jotka edustavat sen sivuja jokaiselle kyseisen kansakunnan neljätoista konfederaation osavaltiolle.

Kovera ja kupera tetradecágonos

Yleensä monikulmiot, kuten tetradecágono, voivat olla kupera tai kovera, ensimmäisessä tapauksessa niiden sisäkulmien mitta ei ylitä 180º. Säännöllinen tetradech on kupera, kuten mikä tahansa tavallinen monikulmio, koska mikä tahansa sen sisäkulma mittaa 154.286º.

Toisaalta koverassa tetradechissä yksi tai useampi sen sisäkulmista on yli 180º.

Numeerinen esimerkki

Annetaan säännöllinen tetradagon, jonka sivu on 5 cm, etsi:

a) kehä
b) Apoteemen mittaus
c) Radiopituus
d) alue

Vastaukset

a) Koska se on tavallinen monikulmio, kehä on:

P = 14 × 5 cm = 70 cm.

b) Yhtälöstä A = 2L_-Lla × Tg (π/14), missä a = 5 cm, apotemi l_-Lla-

Lens_-Lla = A / [2 × TG (π / 14)] = 5 cm / 0.4565 = 21.9064 cm

c) Radio r voidaan laskea a = 2R × Sen (π/14):

R = a / [2 × sin (π / 14)] = 5 cm / 0.4565 = 22.4698 cm

d) Alueelle on useita vaihtoehtoja, esimerkiksi A = (P × L_-Lla)/2:

A = (70 × 21.9064)/2 cm² = 1533.45 cm².

Viitteet

1. Alexander, D. 2013. Geometria. Viides. Painos. Cengage -oppiminen.
2. Arturo -geometria. Yleinen menetelmä monikulmioiden piirtämiseksi. Palautettu YouTubesta.com
3. Keittolaskin. Tavallinen monikulmiolaskin. Palautettu: Calculatorosoup.com.
4. Piirustus. Tavallinen monikulmikone. Palautettu: Piirustus.com.
5. Requena, b. Kovera monikulmio. Toipunut: UniversOformulat.com.
6. Wikipedia. Rakennettava monikulmio. Palautettu: on.Wikipedia.org.