Mekaaninen työ mikä on, olosuhteet, esimerkit, harjoitukset

Hän mekaaninen työ Se määritellään järjestelmän energiatilassa, joka johtuu ulkoisten voimien vaikutuksesta, kuten painovoima tai kitka. Kansainvälisen järjestelmän mekaaniset työyksiköt ovat Newton X -metro tai Joules, lyhennetty J.

Matemaattisesti se määritellään voimavoiman skalaarituotena vektorin siirtymällä. Joo F Se on jatkuva voima ja lens Se on siirtymä, molemmat vektorit, työ W ilmaistaan ​​seuraavasti: W = F ● lens

Kuvio 1. Vaikka urheilija nostaa painoa, hän työskentelee painovoimaa vastaan, mutta kun hän ylläpitää painoa liikkumattomana, fysiikan näkökulmasta hän ei tee työtä. Lähde: NeedPix.com

Kun voima ei ole vakio, meidän on analysoitava työ, kun siirtymät ovat hyvin pieniä tai differentiaalisia. Tässä tapauksessa, jos sitä pidetään lähtökohtana pisteeseen A ja saapuessa kohtaan B, kokonaistyö saadaan lisäämällä kaikki maksut samaan. Tämä vastaa seuraavan integraalin laskemista:

Ja kuten alussa todettiin, jos järjestelmän energiaa tapahtuu, se johtuu siitä, että ulkomailla on voimia, jotka vaikuttavat siihen, siksi:

Järjestelmäenergian vaihtelu = ulkoisten voimien tekemä työ

ΔE = W_alanumero

Kun järjestelmään lisätään energiaa, w> 0 ja kun se vähennetään<0. Ahora bien, si ΔE = 0, puede significar que:

-Järjestelmä on eristetty eikä siihen vaikuta ulkoisia voimia.

-On olemassa ulkoisia voimia, mutta he eivät tee työtä järjestelmän parissa.

Koska energian variaatio vastaa ulkoisten voimien tekemää työtä, yksikkö, jos energia on myös Joule. Tähän sisältyy minkä tahansa tyyppinen energia: kineettinen, potentiaali, lämpö, ​​kemiallinen ja paljon muuta.

[TOC]

Olosuhteet, jotta mekaaninen työ on

Olemme jo nähneet, että työ on määritelty skalaarituotteeksi. Otetaan määritelmä jatkuvan voiman tekemästä työstä ja sovelletaan skalaarituotteen käsite kahden vektorin välillä:

W = F ● L = F.lens.cos θ

Missä F Se on voiman suuruus, lens Se on siirtymän suuruus ja θ Se on kulma, joka on voiman ja siirtymän välillä. Kuvassa 2 on esimerkki kallistetusta ulkoisesta voimasta, joka vaikuttaa lohkoon (järjestelmä), joka tuottaa vaakasuuntaisen siirtymän.

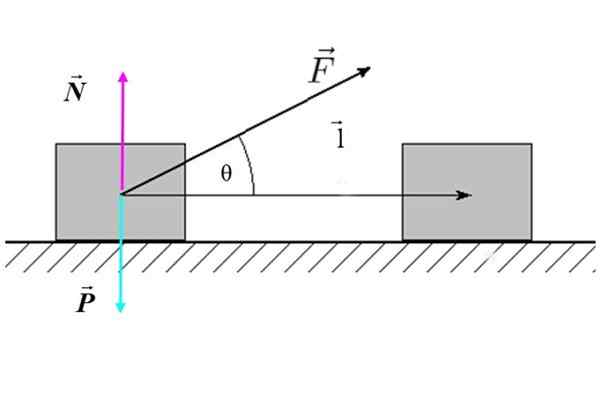Kuva 2. Vapaa rungon kaavio lohkosta, joka liikkuu tasaisella pinnalla. Lähde: f. Zapata.

Teoksen uudelleenkirjoittaminen seuraavasti:

W = (f. cos θ). lens

Voimme vakuuttaa, että vain siirtymän suuntainen voiman komponentti: F. cos θ es pystyy tekemään työtä. Jos θ = 90º, niin cos θ = 0 ja työ olisi mitätön.

Siksi päätellään, että siirtymiseen kohtisuorassa olevat voimat eivät tee mekaanista työtä.

Kuvan 2 tapauksessa eikä normaali voima N eikä paino P Ne toimivat, koska molemmat ovat kohtisuorassa siirtymiseen lens.

Työn merkit

Kuten edellä selitettiin, W - Se voi olla positiivinen tai negatiivinen. Kun cos θ> 0, Voimalla tehty työ on positiivinen, koska sillä on sama suunta liikkeelle.

Se voi palvella sinua: Massumero: Mikä se on ja miten se saa (esimerkkien kanssa)

Joo cos θ = 1, Vahvuus ja siirtymä ovat yhdensuuntaisia ​​ja työ on maksimia.

Jos cos θ < 1, la fuerza no está a favor del movimiento y el trabajo es negativo.

Kun cos θ = -1, Voima on täysin vastakohta siirtymistä, kuten kineettinen kitka, jonka vaikutus on pysäyttää esine, jolla se toimii. Joten työ on minimaalinen.

Tämä on yhtä mieltä siitä, mitä alussa sanottiin: Jos työ on positiivista, järjestelmään lisätään energiaa, ja jos se on negatiivinen, se vähennetään.

Nettotyö W -_netto Se on määritelty kaikkien järjestelmään toimivien voimien tekemien töiden summaksi:

W -_netto = ∑W_Yllyttää

Sitten voimme päätellä, että nettomekaanisen työn olemassaolon takaamiseksi on välttämätöntä, että:

-Ulkoiset voimat toimivat esineeseen.

-Nämä voimat eivät ole kaikki kohtisuorassa siirtymään (cos θ ≠ 0).

-Kunkin voiman tekemiä töitä ei peruuteta toistensa kanssa.

-Siirtymä on.

Mekaaniset työesimerkit

-Aina kun se on asetettava esine liikkeelle lepojen perusteella, on välttämätöntä tehdä mekaaninen työ. Esimerkiksi työntää jääkaappi tai raskas tavaratila vaakasuoralle pinnalle.

-Toinen esimerkki tilanteesta, jossa on tarpeen tehdä mekaaninen työ on muuttaa liikkuvan pallon nopeutta.

-On tarpeen tehdä työtä esineen nostamiseksi tietyllä korkeudella lattialla.

Nyt on yhtä yleisiä tilanteita, joissa Ei työ tehdään, vaikka esiintymiset osoittavat muuten. Olemme sanoneet, että kohteen nostamiseksi tietyllä korkeudella meidän on tehtävä työtä, joten lataamme esineen, nostamme sen pään yläpuolelle ja pidämme sen siellä. Teemmekö töitä?

Ilmeisesti kyllä, koska jos esine on raskas, aseet väsyvät pian, mutta riippumatta siitä, kuinka paljon työtä tehdään, työtä ei tehdä fysiikan näkökulmasta. Miksi ei? Koska esine ei liiku.

Toinen tapaus, jossa siitä huolimatta, että sillä on ulkoinen voima, se ei suorita mekaanista työtä, kun hiukkasella on tasainen pyöreä liike.

Se voi palvella sinua: Normaali työ: mistä se koostuu, miten se lasketaan, esimerkkejä

Esimerkiksi lapsi, joka kääntää kiven sidottuna naruun. Merkin jännitys on keskikeskuksen voima, joka mahdollistaa kiven kiertoa. Mutta aina tämä voima on kohtisuorassa siirtymiseen. Älä siis tee mekaanista työtä huolimatta siitä, että se suosii liikettä.

Työenergian teoria-elokuva

Järjestelmän kineettinen energia on se, mitä sillä on liikkeen alla. Joo m on taikina ja v Se on liikkeen nopeus, kineettinen energia merkitään K -k - Ja sen annetaan:

K = ½ mV²

Määritelmän mukaan esineen kineettinen energia ei voi olla negatiivinen, koska sekä massa että nopeuden neliö ovat aina positiivisia määriä. Kineettinen energia voi olla 0, kun esine on levossa.

Järjestelmän kineettisen energian muuttamiseksi se on välttämätöntä-. Tätä varten on välttämätöntä tehdä nettotyö järjestelmässä, siksi:

W -_netto = ΔK -k -

Tämä on työlause - kineettinen energia. Toteaa, että:

Nettotyö vastaa järjestelmän kineettisen energian muutosta

Huomaa, että vaikka k on aina positiivinen, ΔK voi olla positiivinen tai negatiivinen, koska:

Δk = k_lopullinen - K -k - _alkukirjain

Joo K -k -_lopullinen -K -k - _alkukirjain Järjestelmä on saanut energiaa ja Δk> 0. Päinvastoin, kyllä K -k -_lopullinen < K -k - _alkukirjain, Järjestelmä on tuottanut energiaa.

Työskentely kevään venyttämiseksi

Kun venyttää (tai puristaa) jousta, on tehtävä työ. Tämä työ on tallennettu keväällä, jolloin tämä puolestaan ​​voi tehdä töitä esimerkiksi lohkon kanssa, joka on kiinnitetty yhteen sen päistä.

Hooken laissa todetaan, että jousen aiheuttama joukko on palautusjoukko - se on vastoin siirtymistä - ja myös verrannollinen mainittuun siirtymiseen. Suhteellisuusvakio riippuu siitä, kuinka jousi on: pehmeä ja helposti muodonmuutos tai jäykkä.

Tämän voiman annetaan:

F_{r -} = -kx

Ilmaisussa, F_{r -} Se on voima, k -k - Se on kevään vakio ja x Se on siirtymä. Negatiivinen merkki osoittaa, että jousen aiheuttama voima vastustaa siirtymistä.

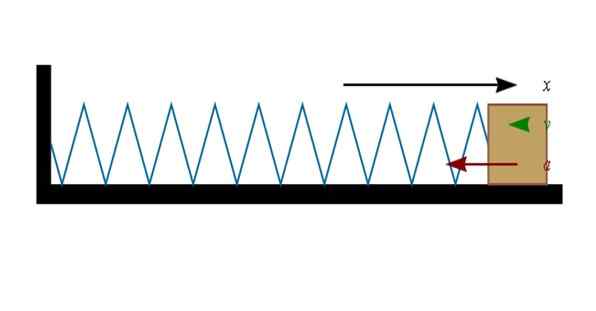Kuva 3. Pakattu tai venytetty jousi toimii sen päähän sidottuun esineeseen. Lähde: Wikimedia Commons.

Jos jousi on pakattu (kuvion vasemmalle), sen päässä oleva lohko siirtyy oikealle. Ja kun jousi on venytetty (oikealla), lohko haluaa siirtyä vasemmalle.

Jotta jousi purkaa tai venyttää, joidenkin ulkoisten edustajien on tehtävä työ, ja koska se on muuttuva voima, tämän työn laskemiseksi sinun on käytettävä alussa tapahtuvaa määritelmää:

Voi palvella sinua: Darcy Law

On erittäin tärkeää huomata, että tämä on ulkoisen aineen (esimerkiksi henkilön käsi) tekemä työ jousen puristamiseksi tai venyttämiseksi. Siksi negatiivinen merkki ei ilmesty. Ja koska sijainnit ovat neliöitä, riippumatta siitä, ovatko ne kompressioita tai pidentymisiä.

Työ, joka tekee kevään vuorotellen lohkoon, on:

W -_kevät = -W_alanumero

Harjoitukset

Harjoitus 1

Kuvion 4 lohkossa on massa m = 2 kg ja liukuu kallistetun tason läpi ilman kitkaa, α = 36.Yhdeksäs. Olettaen, että sen sallitaan liukastua muusta tason yläosasta, jonka korkeus on h = 3 m, etsi nopeus, jolla lohko saavuttaa tason pohjan, työenergialause-energian kinetiikan läpi.

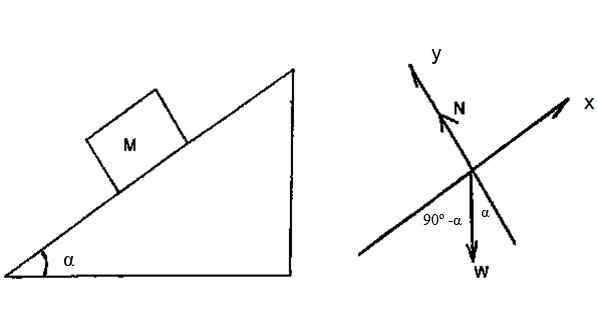Kuva 4. Lohko liukuu alas kaltevalle tasolle hieromatta. Lähde: f. Zapata.

Ratkaisu

Vapaa kehon kaavio osoittaa, että ainoa voima, joka pystyy tekemään työtä lohkossa, on paino. Tarkempi.

Tason lohkon kuljettama etäisyys lasketaan trigonometrialla:

D = 3 / (cos 36.9º) M = 3.75 m

W -_paino = (Mg). d -d. cos (90-a) = 2 x 9.8 x 3.75 x cos 53.1. J = 44.1 J

Työlauseen ja energian kineettinen:

W -_netto = ΔK -k -

W -_netto = W_paino

Δk = ½ mV_F²- ½ MV_jompikumpi²

Koska se julkaistaan ​​lepo, v_jompikumpi = 0, siksi:

W -_netto = ½ MV_F²

Harjoitus 2

Vaakaväki, jonka vakio on k = 750 n/m on kiinnitetty toiseen päähän seinään. Yksi henkilö pakata toisen pään 5 cm: n etäisyydellä. Laske: a) henkilön käyttämä voima, b) työ, jonka hän teki jousen puristamiseksi.

Ratkaisu

a) Henkilön käyttämän voiman suuruus on:

F = kx = 750 n/ m . 5 x 10 ^-2 M = 37.5 n.

b) Jos kevään pää on alun perin x₁ = 0, viedä se sieltä lopulliseen sijaintiin x₂ = 5 cm, seuraava työ on tehtävä edellisessä osassa saadun tuloksen mukaan:

W -_alanumero = ½ k (x₂² - x₁²) = 0.5 x 750 x (0.05² -0 -²) J = 0.9375 J.

Viitteet

1. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Nide 2. Dynaaminen. Toimittanut Douglas Figueroa (USB).
2. Iparraguirre, L. 2009. Perusmekaniikka. Luonnontieteiden kokoelma ja matematiikka. Ilmainen online -jakelu.
3. Ritari, r. 2017. Tutkijoiden fysiikka ja tekniikka: strategialähestymistapa. Pearson.
4. Fysiikka librettexts. Energian lause. Toipunut: Phys.Librettexts.org
5. Työ- ja energia. Toipunut: fysiikka.Bu.Edu
6. Työ, energia ja voima. Palautettu: NCERT.Nivel.sisään