Kotisivu
Matematiikka
Suorakulmion trapetsiominaisuudet, suhteet ja kaavat, esimerkit

Matematiikka

Suorakulmion trapetsiominaisuudet, suhteet ja kaavat, esimerkit

2585
528
Eddie Hackett

Eräs suorakaiteen trapetsi Se on neljän sivun litteä kuva, niin että kaksi niistä on yhdensuuntainen toistensa kanssa, nimeltään pohjat Ja myös yksi muista puolista on kohtisuorassa emäksissä.

Tästä syystä kaksi sisäkulmasta ovat suorat, ts. Ne mittaavat 90º. Siten kuvalle annetun "suorakulmion" nimi. Seuraava kuva suorakulmion trapetsista selventää näitä ominaisuuksia:

[TOC]

Trapetsin elementit

Trapezoidin elementit ovat:

-Pohjat

-Kärjet

-Korkeus

-Sisäkulmat

-Keskimääräinen pohja

-Diagonaalit

Yksityiskohtaisesti nämä elementit kuvioiden 1 ja 2 avulla:

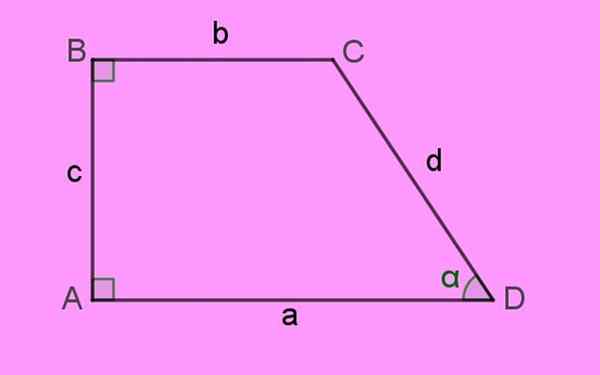
Kuvio 1. Suorakulmion trapetsi, jolle on tunnusomaista kaksi sisäkulmaa 90º: a ja b. Lähde: f. Zapata.

Suorakulmion trapetsoidin sivut on merkitty pienillä kirjaimilla A, B, C ja D. Kuvion kulmat tai Kärjet Ne on ilmoitettu isoilla kirjaimilla. Lopuksi Sisäkulmat Ne ilmaistaan kreikkalaisilla kirjaimilla.

Määritelmän mukaan pohjat Tästä trapezoidista ovat sivut A ja B, jotka havaitut ovat yhdensuuntaisia ja myös eripituisia.

Kohtisuora puoli molemmille emäksille on puoli c vasemmalla, mikä on korkeus h trapetsia. Ja lopuksi on sivu D, joka muodostaa akuutin kulman α sivulla A.

Summa Sisäkulmat nelinkertainen on 360º. On helppo ymmärtää, että puuttuva kulma C kuvassa on 180 - α.

Se keskimääräinen pohja Segmentti liittyy ei -rinnakkaisten sivujen keskipisteisiin (EF -segmentti kuvassa 2).

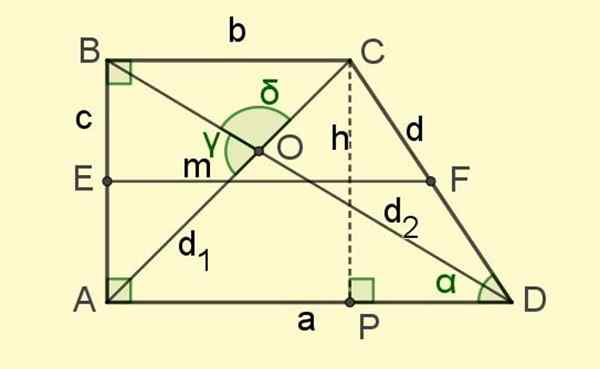Kuva 2. Suorakulmion elementit trapezoidi. Lähde: f. Zapata.

Ja lopuksi on diagonaalit d₁ ja D₂, segmentit, jotka yhdistävät vastakkaiset kärkipisteet ja leikkaavat pisteessä O (katso kuva 2).

Suhteet ja kaavat

Trapetsin korkeus H

H = c

Kehä p

Se on muodon mitta ja lasketaan lisäämällä sivut:

Kehä = a + b + c + d

Puoli d -d Se ilmaistaan korkeuden tai puolen suhteen c Pythagoras -lauseen kautta:

D = √ (a-b)² + c²

Korvaaminen kehällä:

P = a + b + c + √ (a-b)² + c²

Keskimääräinen pohja

Se on emäksen puolivälissä:

Keskipitkä pohja = (a+b)/2

Joskus tällä tavalla ilmaistu keskimääräinen pohja on löydetty:

Keskimääräinen pohja = (tärkein emäs + vähäinen pohja) /2

Alue

Trapetsin alue A on keskimääräisen pohjan tuote korkeudesta:

A = (Tärkein pohja + vähäinen pohja) x korkeus /2

A = (a+b) c/2

Diagonaalit, sivut ja kulmat

Useita kolmioita esiintyy kuviossa 2, sekä suorakulmiot että ei -suorakulmiot. Pythagoras -lause ja ne, jotka eivät ole, niille, jotka ovat oikeassa kolmiossa.

Voi palvella sinua: Transcendent -numerot: Mitä ovat, kaavat, esimerkit, harjoitukset

Tällä tavoin sivujen ja trapezion sivujen ja sivujen ja sisäkulmien välillä on suhteita.

CPA -kolmio

Se on suorakulmio, sen jalat ovat samat ja ne ovat B: n arvoisia, kun taas hypotenuse on diagonaalinen D₁, siksi:

d -d₁² = b² + b -² = 2b²

Kouru

Se on myös suorakulmio, jalat ovat -lla ja c (tai myös -lla ja h) Ja hypotenuse on D₂, jotta:

d -d₂² = a² + c²= a² + h²

CDA -kolmio

Koska tämä kolmio ei ole suorakulmio, kosinuslause levitetään tai myös rinta.

Coseno -lauseen mukaan:

d -d₁² = a² + d -d² - 2AD cos α

CDP -kolmio

Tämä kolmio on suorakulmio ja sen sivuilla kulman α trigonometriset syyt on rakennettu:

sin α = h/d

cos α = pd/d

Mutta PD = A - B -puoli, siksi:

cos α = (a -b) / d → a - b = d cos α

a = b + d cos α

Sinulla on myös:

TG α = sin α / cos α = h / (a-b) → h = tg α (a-b)

CDB -kolmio

Tässä kolmiossa meillä on kulma, jonka kärkipiste on C: ssä. Sitä ei ole merkitty kuvassa, mutta alussa se erottui, että se on 180 - α arvoinen. Tämä kolmio ei ole suorakulmio, joten kosininlause tai rintalause voidaan käyttää.

Nyt voidaan helposti osoittaa, että:

SEN (180 - α) = sin α

cos (180 - α) = - cos α

Coseno -lauseen soveltaminen:

d -d₂² = D² + b -²- 2DB COS (180 - α) = D² + b -²+ 2DB COS α

Esimerkkejä suorakulmioista

Trapezioja ja erityisesti suorakulmioita löytyy monilta puolilta, ja joskus eivät aina konkreettisia. Täällä meillä on useita esimerkkejä:

Trepecio suunnitteluelementtinä

Geometrisia hahmoja on runsaasti lukuisten rakennusten arkkitehtuurissa, kuten tämä New Yorkissa.

Myös trapetsoidinen muoto on yleinen konttien, astioiden, terien (terien (terien (Leikkuri tai tarkka), arkit ja graafisessa suunnittelussa.

Kuva 3. Enkeli suorakulmion trapetsoidissa New Yorkin kirkossa. Lähde: David Goehring Flickrin kautta.

Trapetsoidinen aaltogeneraattori

Sähkösignaalit eivät voi olla vain neliömäisiä, sinia tai kolmionmuotoisia. On myös trapetsoidisia signaaleja, jotka ovat hyödyllisiä lukuisissa piireissä. Kuviossa 4 on trapetsoidinen signaali, joka koostuu kahdesta suorakulmusta. Niiden välillä ne muodostavat yhden šosceles trapezoidin.

Voi palvella sinua: 8: 8: Mitkä ovat helppoja selityksiä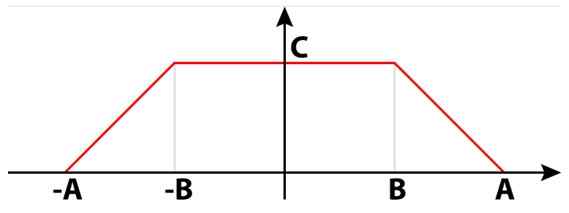

Kuva 4. Trapetsoidinen signaali. Lähde: Wikimedia Commons.

Numeerisessa laskelmassa

Numeerisesti laskemiseksi funktion f (x) määritellyt integraalit A: n ja B: n välillä, trapetsisääntöä käytetään likimääräiseen alueeseen F (x) -kaavion alla. Seuraavassa kuvassa vasemmalla vasemmalla integraalit lähestymistavat yhdellä suorakulmiolla trapezoidilla.

Parempi lähestymistapa on oikea kuva, useilla suorakulmoilla.

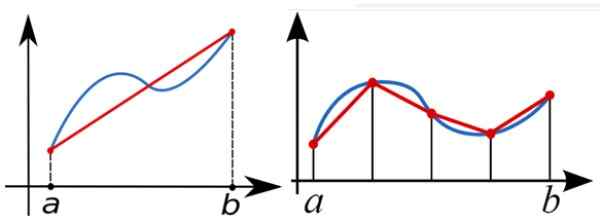Kuva 5. Määritelty integraali A: n ja B: n välillä ei ole muuta kuin käyrän f (x) -alueen alueella näiden arvojen välillä. Suorakulmion trapetsoidi voi toimia ensimmäisenä lähestymistapana kyseiselle alueelle, mutta mitä enemmän trapetsoideja käytetään, sitä parempi lähestymistapa. Lähde: Wikimedia Commons.

Trapetsoidinen kuormituspalkki

Voimat eivät aina keskittyy yhteen pisteeseen, koska niiden toiminnassa olevilla ruumiilla on huomattavia ulottuvuuksia. Näin on sillan, jonka läpi ajoneuvot kiertävät jatkuvasti, uima -altaan vesi saman seinällä tai katto, johon vesi tai lumi kerääntyy.

Siksi voimat jakautuvat pituuden, pinnan tai tilavuuden yksikköä kohti riippuen siitä, että ne toimivat.

Palkin tapauksessa pituusyksikköä kohti jakautuneella voimalla voi olla erilaisia jakautumisia, esimerkiksi alla esitetty suorakulmion trapetsia:

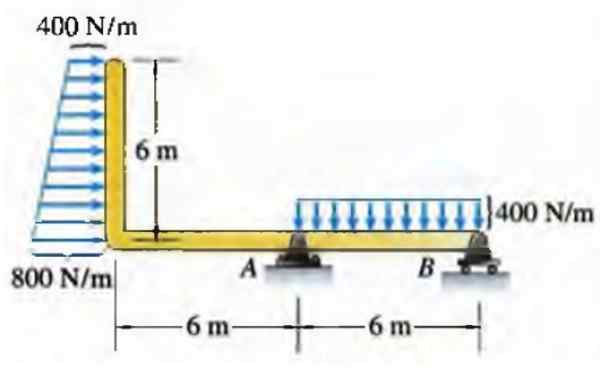Kuva 6. Kuorma palkkiin. Lähde: Bedford,. 1996. Staattinen. Addison Wesley Inter -American.

Todellisuudessa ei aina jakautuminen vastaa säännöllisiä geometrisia muotoja, mutta ne voivat olla monissa tapauksissa hyvä lähestymistapa.

Koulutus- ja oppimisvälineenä

Lohkot ja arkit, joissa on geometriset muodot, trapetsoidit mukaan lukien.

Kuva 7. Lohkot yksinkertaisilla geometrisilla muodoilla. Kuinka monta suorakulmiota on piilotettu lohkoihin? Lähde: Wikimedia Commons.

Ratkaisut

- Harjoitus 1

Kuvion 1 suorakulmion trapetsoidissa suurin pohja on 50 cm: n arvoinen ja pienin emäs on yhtä suuri kuin 30 cm, on myös tiedossa, että vino sivumitta on 35 cm. Löytö:

a) kulma α

b) korkeus

c) kehä

d) Keskikokoinen pohja

e) alue

f) diagonaali

Liittää jhk

Lausuntotiedot on tiivistetty tällä tavalla:

A = korkeampi pohja = 50 cm

B = pieni pohja = 30 cm

D = kalteva puoli = 35 cm

Voi palvella sinua: Perusoperaatiot

Kulman α löytämiseksi vierailemme kaavoissa ja yhtälöissä osassa nähdäksemme kumpi, joka parhaiten sopii tarjottuihin tietoihin. Epäselmäkulma löytyy useista analysoiduista kolmioista, esimerkiksi CDP.

Siellä meillä on tämä kaava, joka sisältää tuntemattoman ja myös tuntemamme tiedot:

cos α = (a-b) / d

Siksi:

α = kaaret [(a-b) / d] = kaaret [(50-30) / 35] = kaaret 20/35 = 55.15 º

Ratkaisu b

Yhtälöstä:

sin α = h/d

H = D.synti α = 35 Sen 55.15 º cm = 28.72 cm

Liuos C

Ympäristö on sivujen summa, ja koska korkeus on yhtä suuri kuin sivu C, meidän on:

C = H = 28.72 cm

Siksi:

P = (50 + 30 + 35 + 28.72) CM = 143.72 cm

Liuos D

Keskimääräinen pohja on emäksen puolivälissä:

Keskipitkä pohja = (50 + 30 cm)/2 = 40 cm

Ratkaisu E

Trapetsoidinen alue on:

A = keskimääräinen pohja x korkeus = 40 cm x 28.72 = 1148.8 cm².

Liuos f

Diagonaalille d₁ Tätä kaavaa voidaan käyttää:

d -d₁² = b² + b -² = 2b²

d -d₁²= 2 x (30 cm)² = 1800 cm²

d -d₁ = √1800 cm² = 42.42 cm

Ja diagonaalille D₂-

d -d₂² = D² + b -²+ 2DB COS α = (35 cm)² + (30 cm)² + 2 x 35 x 30 cm² Cos 55.15 º = 3325 cm²

d -d₂ = √ 3325 cm² = 57.66 cm

Tämä ei ole ainoa tapa löytää d₂, koska siellä on myös DAB -kolmio.

- Harjoitus 2

Seuraava nopeuskaavio siirrettävästä riippuen, jolla on tasaisesti kiihtynyt suoraviivainen liike. Laske matkapuhelimen kulkemat etäisyydet ajanjakson välillä 0.5 ja 1.2 sekuntia.

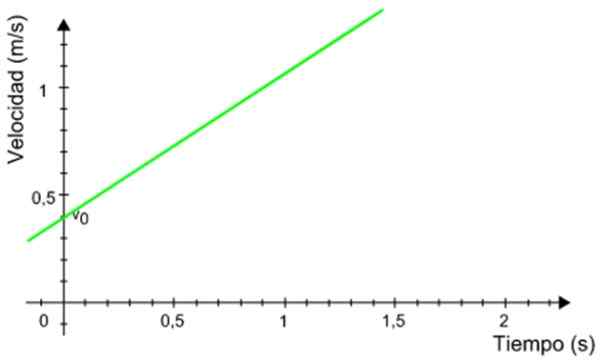Kuva 8. Graafinen matkapuhelimen aikaa vastaan tasaisesti kiihdytetyllä REKNET -liikkeellä. Lähde: Wikimedia Commons.

Ratkaisu

Matkapuhelimen kuljettama etäisyys vastaa kaavion alla olevaa aluetta, joka on rajattu ilmoitetulla aikavälillä.

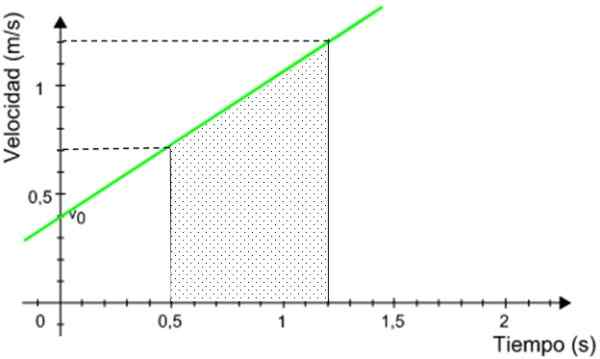Kuva 9. Matkapuhelimen kuljettama etäisyys vastaa grafiikan alla olevaa aluetta. Lähde: Muokattu f. Zapata.

Varjostettu alue on suorakulmion trapetsoidin alue, jonka on annettu: