Fyysisen radan ominaisuudet, tyypit, esimerkit ja harjoitukset

Se Fysiikan etenemissuunta Se käyrä kuvaa liikkuvasta kulkiessaan peräkkäisiä pisteitä sen liikkeen aikana. Koska tämä voi omaksua lukemattomia variantteja, ne ovat myös suuntauksia, joita matkapuhelin voi seurata.

Siirtyäkseen paikasta toiseen, henkilö voi kulkea erilaisia ​​polkuja ja erilaisia ​​tapoja: jalka kaduilla ja keinoilla olevien jalkakäytävien läpi tai saapuminen autolla tai moottoripyörällä moottoritiellä. Metsän läpi kulkevan matkan aikana kävelijä voi seurata monimutkaista etenemissuuntausta, joka sisältää käännökset, kiipeämisen tai pudottamisen ja kunnes hän kulkee useita kertoja saman pisteen läpi.

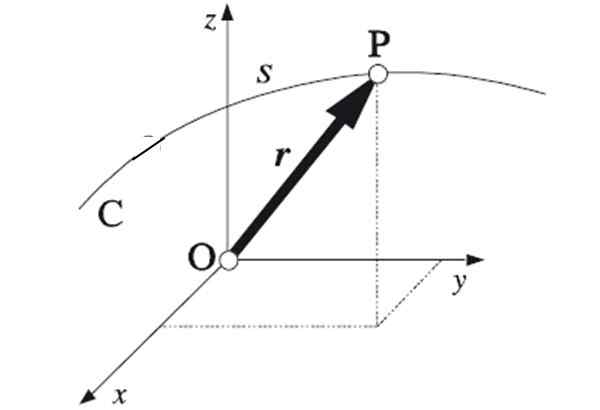Kuvio 1. Yhdistämällä kunkin sijaintivektorin äärimmäiset pisteet, hiukkasen ja. Lähde: Algarabia [julkinen alue]

Jos pisteet, joiden kautta matkapuhelin kulkee, seuraavat suoraa linjaa, suuntaus on suoraviivainen. Tämä on yksinkertaisin etenemissuunta, koska se on yksi ulottuvuus. Aseman määrittäminen vaatii yhden koordinaatin.

Mutta matkapuhelin voi seurata kurvikas etenemissuuntausta, joka on suljettu tai avoin,. Näissä tapauksissa aseman seuranta vaatii kaksi tai kolme koordinaattia. Nämä ovat vastaavasti liikkeitä tasossa ja tilassa. Tämän kanssa on linkit: Liikkeen aineellisten olosuhteiden rajoittaminen. Joitakin esimerkkejä ovat:

- Auringon ympärillä olevat planeettoja kuvaavat kiertoradat ovat suljettuja ellipsin muotoisia suuntauksia. Vaikka joissain tapauksissa ne voivat arvioida pyöreän, kuten maan tapauksessa.

- Pallo, jonka maalivahti potkaisee maalipotkun, seuraa parabolista etenemissuuntausta.

- Lennon lintu kuvaa avaruudessa kaarevia suuntauksia, koska lentokoneella liikkumisen lisäksi se voi nousta tai alhaisemmalla tasolla tahdon mukaan.

Fysiikan etenemissuunta voidaan ilmaista matemaattisesti, kun liikkuva asema tunnetaan milloin tahansa. Olla r - Sijaintivektori, jolla puolestaan ​​on koordinaatit x, ja ja z -z Kolmen dimensionaalisen liikkeen yleisimmässä tapauksessa. Toiminnon tunteminen r - (T) Etenemissuunta määritetään kokonaan.

[TOC]

Kaverit

Yleisesti ottaen suunta voi olla melko monimutkainen käyrä, varsinkin jos haluat ilmaista matemaattisesti. Siksi se alkaa yksinkertaisimmista malleista, joissa matkapuhelimet kulkevat suoralla linjalla tai lentokoneella, joka voi olla lattia tai mikä tahansa muu sopiva:

Liikkeet yhdessä, kaksi ja kolme ulottuvuutta

Tutkituimpia suuntauksia ovat:

- Suorakulmainen, Kun matkustat vaakasuoralla, pystysuoralla tai kaltevalla viivalla. Pallo, joka heitetään pystysuoraan ylöspäin tämän suuntauksen tai esineen, joka liukuu alamäkeen myös kaltevalla tasolla. Ne ovat yhden ulottuvuuden liikkeitä, yksi koordinaatti riittää määrittämään sen sijainti kokonaan.

- Parabolinen, jossa matkapuhelin kuvaa parabolakaaria. Se on usein, koska kaikki esineet, jotka käynnistettiin vinosti painovoiman (ammus) nojalla, seuraa tätä suuntausta. Määrittääksesi mobiililaitteen sijainnin, sinun on annettava kaksi koordinaattia: x ja ja.

- Pyöreä, tapahtuu, kun liikkuva hiukkas seuraa kehää. Se on myös yleistä luonteeltaan ja päivittäisessä käytännössä. Monet jokapäiväiset esineet seuraavat pyöreää etenemissuuntausta, kuten renkaita, koneet ja satelliitit kiertoradalla, antamaan joitain esimerkkejä.

Voi palvella sinua: varustevektorit: Määritelmä, merkintä, harjoitukset

- Elliptinen, Esine liikkuu ellipsin jälkeen. Kuten alussa todettiin, planeetat seuraavat kiertoradalla auringon ympärillä.

- Hyperbolinen, Tähtitieteelliset esineet keskusvoiman (painovoima) vaikutuksesta voivat seurata elliptisiä (suljettuja) tai hyperbolisia (avoimia) suuntauksia, nämä ovat harvemmin kuin ensimmäiset.

- Kiero-, o Kierre, kuten lintu, joka nousee lämpövirrassa.

- Heiluttaa tai riipus, Matkapuhelin kuvaa kaaria edestakaisen matkan liikkeissä.

Esimerkit

Edellisessä osassa kuvattuja suuntauksia on erittäin hyödyllinen saadaksesi kuvan nopeasti siitä, kuinka esineen liikkeet ovat. Joka tapauksessa on tarpeen selventää, että matkapuhelimen etenemissuunta riippuu tarkkailijan sijainnista. Tämä tarkoittaa, että sama tapahtuma voidaan nähdä eri tavoin, missä kukin on.

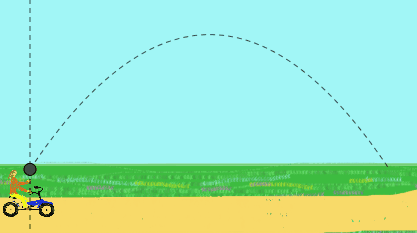
Esimerkiksi tyttöpoljin vakiona nopeudella ja heittää pallon. Hän huomauttaa, että pallo kuvaa suoraviivaista etenemissuuntausta. 

Kuitenkin tarkkailijalle, joka seisoo sitä, pallo on kuitenkin parabolinen liike. Hänelle pallo heitettiin alun perin kaltevalla nopeudella, tytön käden nopeuden seurauksena plus polkupyörän nopeus.

Kuva 2. Tämä animaatio osoittaa tytön tekemän pallon pystysuuntaisen käynnistyksen, joka menee polkupyörällä, kuten hän näkee (suoraviivainen suunta) ja kuten näet tarkkailijan (parabolinen suunta). (Valmistettu f. Zapata).

Matkapuhelimen etenemissuuntainen, implisiittinen ja parametrinen tapa

- Selkeä, Suoraan yhtälön antaman käyrän tai geometrisen paikan määrittäminen ja (x)

- Implisiittinen, jossa käyrä ilmaistaan f (x, y, z) = 0

-Parametrinen, Tällä tavoin X- ja Y Z -koordinaatit tapahtuvat parametrista riippuen, jotka yleensä valitaan ajankohtana t. Tässä tapauksessa suunta koostuu toiminnoista: x (t), ja T) ja z (t).

Seuraavaksi kaksi erittäin tutkittua suuntausta on yksityiskohtaisesti kuvata elokuvateatterissa: parabolinen etenemissuunta ja pyöreä rata.

Käynnistyminen tyhjiössä

Objekti (ammus) heitetään muodostaen kulman A vaakasuoran ja alkuperäisen nopeuden kanssa v_jompikumpi Kuten kuva näyttää. Ilmankestävyyttä ei oteta huomioon. Liikettä voidaan käsitellä kahtena riippumattomana ja samanaikaisena liikkeessä: yksi vaakasuora vakiona ja toisella pystysuoralla nopeudella painovoiman vaikutuksen alla.

x (t) = x_jompikumpi +v_härkä.t

ja (t) = y_jompikumpi +v_Oy.T -½ g.t²

Nämä yhtälöt ovat parametriset yhtälöt ammuksen käynnistämisestä. Kuten edellä selitettiin, heillä on yhteinen parametri t, mitä on aika.

Kuvan oikeassa kolmiossa seuraava voidaan nähdä:

v_härkä = v_jompikumpi cos θ_Yllyttää

v_Oy = v_jompikumpi synti θ_Yllyttää

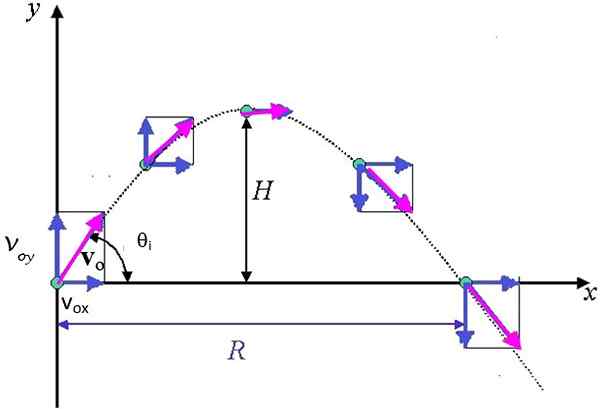Kuva 3. Parabolinen etenemissuunta, jota seuraa ammus, joka näyttää nopeusvektorin komponentit. H on maksimiarvo ja R -korkeus on maksimaalinen vaakasuuntainen ulottuvuus. Lähde: Ayush12gupta [CC BY-SA 4.0 (https: // creativecommons.Org/lisenssit/by-SA/4.0)]

Korvaamalla nämä yhtälöt, jotka sisältävät käynnistyskulman parametrisissä yhtälöissä, se on:

Voi palvella sinua: äänen diffraktio: Mikä on, esimerkkejä, sovelluksia

x (t) = x_jompikumpi +v_jompikumpi cos θ_Yllyttää.t

ja (t) = y_jompikumpi +v_jompikumpi. synti θ_Yllyttää.T -½ g.t²

Parabolinen radan yhtälö

Suuntaradan nimenomainen yhtälö on x (t) -yhtälön T T: n puhdistaminen ja Y (t) -yhtälön (t) korvaaminen (t). Algebrallisen työn helpottamiseksi voidaan olettaa, että alkuperä (0,0) on laukaisupisteessä ja tällä tavalla x_jompikumpi = y_jompikumpi = 0.

Parametrin yksinkertaistamisen jälkeen "t”Se on eliminoitu ja jäljellä oleva yhtälö on ja riippuen X: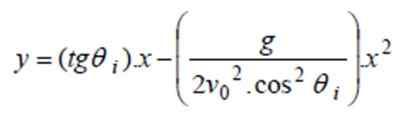

Tämä on suuntayhtälö Selkeä muoto.

Pyöreä suuntaus

Pyöreä suuntaus antaa:

(X - x_jompikumpi-A² + (ja ja_jompikumpi-A² = R²

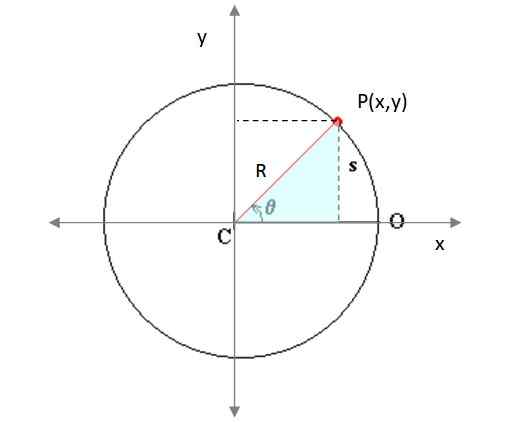Kuva 4. Hiukkas liikkuu ympyränmuotoisella tasolla tasossa. Lähde: Muokattu f. Wikimedia Commons Shoe.

Täällä x_jompikumpi ja ja_jompikumpi Ne edustavat liikkuvan ja r. P (x, y) on suuntauspiste. Varjostetusta suorakulmiokolmiosta (kuva 3) varoitetaan, että:

x = r. cos θ

y = r. synti θ

Parametri on tässä tapauksessa pyyhkäisykulma θ, jota kutsutaan kulma -siirtymäksi. Erityisesti, että kulmanopeus ω (kulma pyyhkäisy aikayksikköä kohti) on vakio, voidaan vahvistaa, että:

θ = θ_jompikumpi + Ωt

Missä θ_jompikumpi Se on hiukkasen alkuperäinen kulma -asema, joka otetaanna 0: ksi, pienenee:

θ = ωt

Tässä tapauksessa aika palaa parametrisiin yhtälöihin, kuten:

x = r.cos ωt

y = r. synti ωt

Yksikkövektorit Yllyttää ja J - Ne ovat erittäin käteviä kirjoittaa objektin sijaintitoiminto r - (T). Ne osoittavat akselin ohjeet x ja akselilla ja vastaavasti. Sen ehdoilla hiukkasen sijainti, joka kuvaa tasaista pyöreää liikettä, on:

r - (t) = r.cos ωt Yllyttää + R -. synti ωt J -

Ratkaisut

Liikunta ratkaistiin 1

Tykki voi ampua luodin nopeudella 200 m/s ja kulma 40º vaakasuoraan nähden. Jos laukaisu suoritetaan tasaisella maastolla ja ilman vastus on halveksittava, etsi:

a) Suuntayhtälö ja (x) ..

b) parametriset yhtälöt x (t) ja ja T).

c) Vaaka -alue ja aika, jonka ammus kestää ilmassa.

d) Korkeus, jolla ammus sijaitsee, kun x = 12.000 m

Ratkaisu)

A) Edellisen osan yhtälössä Y (x): n arvot korvataan: korvataan: korvataan:

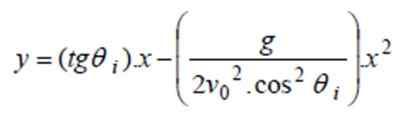
ja (x) = tg 40º. x - 9.8/(2 '400². koos²40º) x² ⇒  ja (x) = 0.8391 x - 0.0000522x²

Ratkaisu b)

b) Käynnistyspiste valitaan koordinaattijärjestelmän alkuperästä (0,0):

x (t) = x_jompikumpi +v_härkä.T = 400'Cos 40º.T = 306.42. t.

ja (t) = y_jompikumpi +v_Oy.T -½ g.t²= 400 'Sen 40º.T - 0.5 9.8't²= 257.12 t - 4.9.t²

Liuos c)

c) Löydä aika, jolloin ammus kestää ilmassa, se on tehty ja (t) = 0, Käynnistyksenä on tasainen maasto:

Voi palvella sinua: mikä on suhteellinen ja ehdoton karheus?

0 = 257.12.T - 4.9.t²

T = 257.12/4.9 s = 52.473 S

Vaakasuuntainen enimmäisalue korvaa tämän arvon x (t):

x_Max = 306.42'52.47 m = 16077.7 m

Toinen tapa löytää x_Max Se tekee suoraan y = 0 suuntausyhtälössä:

0 = 0.8391 x_Max - 0 -.0000522 x²_Max

x = 0.8391 /0.0000522 M = 16078.5m

Desimaalien pyöristämisen vuoksi on pieni ero.

D) liuos

d) Korkeuden tuntemiseksi, kun x = 12000 m tämä arvo korvataan suoraan suuntayhtälössä:

ja (12000) = 0.8391'12000 - 0.0000522'12000² M = 2552.4 m

Liikunta ratkaistiin 2

Objektin sijaintitoiminto annetaan:

r - (t) = 3T Yllyttää + (4 -5T²-A J - m

Löytö:

a) suuntauksen yhtälö. Mikä käyrä on?

b) Alkupaikka ja sijainti, kun t = 2 s.

c) T = 2 s: n jälkeen tehty siirtymä.

Ratkaisu

a) Sijoitusfunktio on annettu yksikkövektorien suhteen Yllyttää ja J -, jotka määrittävät akselien osoitteen x ja ja, siksi:

x (t) = 3T

ja T) = 4 -5T²

Etenemissuuntainen yhtälö ja (x) Hän selvittää t - x (t) ja korvaaminen ja T):

T = x/3

ja (x) = 4 -5. (x/3)² = 4 - 5x²/9 (vertaus)

b) Alkupaikka on: r - (2) = 4 J - m ; Sijainti T = 2 s On r - (2) = 6 Yllyttää -16 J - m

c) siirtymä D -dr - Se on kahden sijaintivektorin vähennys:

Δr - = r - (2) - r - (2) = 6 Yllyttää -16 J -- 4 J - = 6 Yllyttää - kaksikymmentä J - m

Liikunta ratkaistiin 3

Maalla on säde r = 6300 km ja tiedetään, että sen liikkeen kiertojakso on yksi päivä. Löytö:

a) Maan pinnan pisteen suuntauksen yhtälö ja sen sijaintitoiminto.

b) Mainitun pisteen nopeus ja kiihtyvyys.

Ratkaisu)

a) Pyöreän kiertoradan kohdan sijaintifunktio on:

r - (t) = r.cos ωt Yllyttää + R -.synti ωt J -

Sinulla on maan säde r, mutta ei kulmanopeutta ω, mutta se voidaan kuitenkin laskea ajanjaksosta tietäen, että pyöreälle liikkeelle on pätevä sanoa, että:

Ω = 2π × Taajuus = 2π / jakso

Liikevaihto on: 1 päivä = 24 tuntia = 1440 minuuttia = 86400 sekuntia, siksi:

Ω =  2π / 86400 s = 0.000023148 ​​S^-1

Paikkatoiminnon korvaaminen:

r - (t) = r.cos ωt Yllyttää + R -. synti ωt J = 6300 (cos 0.000023148t Yllyttää + synti 0.000023148t J -) Km

Polku parametrisessa muodossa on:

x (t) = 6300. cos 0.000023148t

ja (t) = 6300. synti 0.000023148t

Ratkaisu b)

b) Pyöreän liikkeen osalta lineaarisen nopeuden suuruus v piste liittyy kulmanopeuteen W - kautta:

v = ΩR = 0.000023148 ​​S^-1'6300 km = 0.1458 km/s = 145.8 m/s

Jopa jatkuva liike 145.8 m/s, On kiihtyvyys, joka osoittaa pyöreän kiertoradan keskustaan, joka on vastuussa pyörimispisteen pitämisestä. Se on centripetaalinen kiihtyvyys -lla_c, antama:

-lla_c = v² / R = (145.8 m/s)² / 6300 × 10³ M = 0.00337 m/s².

Viitteet

1. Giancoli, D. Fysiikka. (2006). Periaatteet hakemuksissa. 6^th Prentice Hall. 22-25.
2. Kirkpatrick, L. 2007. Fysiikka: Katsaus maailmaan. 6^ta Lyhennetty painos. Cengage -oppiminen. 23 - 27.
3. Resnick, r. (1999). Fyysinen. Osa 1. Kolmas painos espanjaksi. Meksiko. Mannertoimitusyhtiö S.-Lla. C: n.V. 21-22.
4. Rex, a. (2011). Fysiikan perusteet. Pearson. 33 - 36
5. Sears, Zemansky. (2016). Yliopiston fysiikka, jolla on moderni fysiikka. 14^th. Ed. Osa 1. 50 - 53.
6. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Osa 1. 7^mehu. Painos. Meksiko. Cengage Learning Editors. 23-25.
7. Serway, R., ULOLE, c. (2011). Fysiikan perusteet. 9^naa Ed. Cengage -oppiminen. 43 - 55.
8. Wilson, J. (2011). Fysiikka 10. Pearson -koulutus. 133 - 149.