Etenemissuunta ja siirtymä

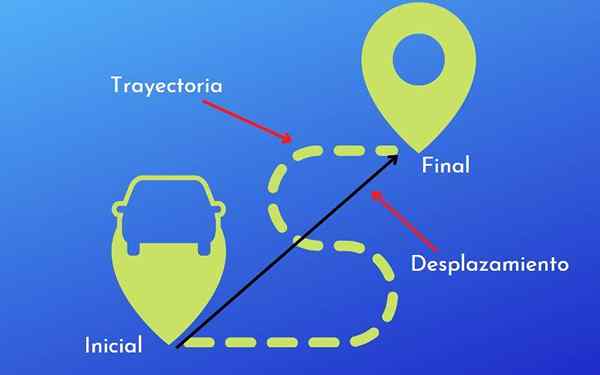
Ero radan ja siirtymisen välillä. Lisenssillä

Se Ero radan ja siirtymisen välillä on se, että jälkimmäinen on esineen kuljettama etäisyys ja suunta, kun taas etenemissuunta on reiti.

Siirtymisen ja etenemissuunnan välillä on kuitenkin selkeämpiä eroja, on parempi selittää esimerkkien avulla, jotka mahdollistavat molempien termien paremman ymmärtämisen.

Siirtymä

Se ymmärretään esineen kuljettamana etäisyydellä ja suunnana ottaen huomioon sen alkuperäinen sijainti ja lopullinen sijainti, aina suorassa linjassa. Sen laskentaa varten, koska se on vektorin suuruus, käytetään senttimetrejä, mittareita tai kilometrejä,.

Siirtymisen laskentakaava määritellään seuraavasti:

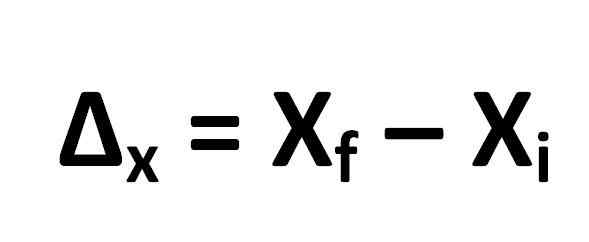
Josta se seuraa sitä:

- Δ_x = siirtymä

- X_F = objektin lopullinen sijainti

- X_Yllyttää = Alkuperäinen objektin sijainti

Esimerkki siirtymästä

1. Jos ryhmä lapsia on reitin alussa, jonka alkuperäinen sijainti on 50 m, liikkuu suorassa linjassa, määrittäen siirtymä jokaisessa kohdassa x_F. 

- X_F = 120 m

- X_F = 90 m

- X_F = 60 m

- X_F = 40 m

2. Ongelmatiedot poistetaan korvaamalla x: n arvot₂ ja x₁ Siirtymäkaavassa:

- Δ_x = ?

- X_Yllyttää = 50 m

- Δ_x = X_F - X_Yllyttää

- Δ_x = 120 m - 50 m = 70 m

3. Tässä ensimmäisessä lähestymistavassa sanomme, että δ_x Se on yhtä suuri kuin 120 m, mikä vastaa ensimmäistä arvoa, jonka löydämme X: stä_F, vähemmän 50 m, joka on x: n arvo_Yllyttää, Se johtaa 70 metriin, toisin sanoen, kun saavutti 120 metriä, siirtymä oli 70 m oikealla.

Voi palvella sinua: laboratoriohaara

4. Jatkamme ratkaisua samalla tavalla B: n, C: n ja D: n arvoille

- Δ_x = 90 m - 50 m = 40 m

- Δ_x = 60 m - 50 m = 10 m

- Δ_x = 40 m - 50 m = - 10 m

Tässä tapauksessa siirtymä antoi meille negatiivisen, mikä tarkoittaa, että lopullinen sijainti on alkuperäisen asennon vastakkaiseen suuntaan.

Suunta

Se on objektin määrittelemä reitti tai linja sen liikkeen ja sen arvioinnin aikana kansainvälisessä järjestelmässä, se käyttää yleensä geometrisiä muotoja, kuten linja, vertaus, ympyrä tai ellipsi.

Se tunnistetaan kuvitteellisen linjan kautta ja olemalla skalaarinen määrä mitataan metreinä.

On huomattava, että radan laskemiseksi meidän on tiedettävä, onko ruumis levossa vai liikkumisessa, ts. Se toimitetaan valitsemassamme referenssijärjestelmässä.

Yhtälö esineen laskemiseksi kansainvälisessä järjestelmässä on annettu:

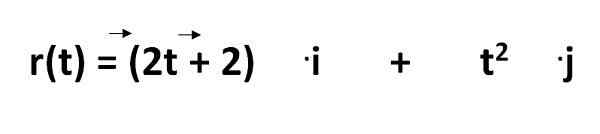
Joista meidän on:

- R (t) = se on suuntayhtälö yhtälö

- 2T - 2 ja T² = edusta koordinaatit ajan funktiona

-  ^.minä ja ^.J = ovat yksikkövektoreita

Ymmärtääksemme esineen kulkevan etenemissuunnan laskelman kehitetään seuraavan esimerkin:

Laske seuraavien sijaintivektoreiden radan yhtälö:

- R (t) = (2T + 7) ^.i + t^{2 .}J -

- R (t) = (t - 2) ^.T & K 2T ^.J -

Ensimmäinen vaihe: Koska suuntayhtälö on x: n funktio, jotta tämä määrittelee vastaavasti X: n ja Y: n arvot jokaisessa nostetussa vektorissa:

1. Ratkaise ensimmäinen sijaintivektori:

- R (t) = (2T + 7) ^.i + t^{2 .}J -

2. Ty = f (x), missä x annetaan yksikkövektorin pitoisuudella ^.I E ja se antaa yksikkövektorin sisältöä ^.J:

Voi palvella sinua: ad hoc: termin alkuperä, merkitykset ja esimerkit käytöstä

- X = 2T + 7

- Y = t²

3. y = f (x), toisin sanoen aika ei ole osa lauseketta, siksi meidän on puhdistettava se, meillä on:

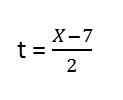
4. Korvaamme puhdistuman sisään ja. Pysyvät:

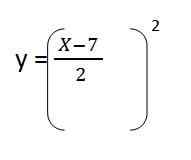
5. Ratkaisemme sulujen sisällön ja meillä on ensimmäisen yksikkövektorin tuloksena olevan etenemissuunnan yhtälö:

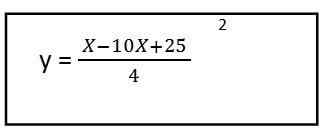
Kuten voimme nähdä, se johti toisen asteen yhtälöön, tämä tarkoittaa, että suuntaus on parabolin muotoon.

Toinen vaihe: Jatkamme samalla tavalla toisen yksikkövektorin etenemissuunnan laskemiseksi:

1. R (t) = (t - 2) ^.T & K 2T ^.J -

- X = t - 2

- Y = 2T

2. Aikaisemmin y = f (x) -vaiheiden seurauksena meidän on puhdistettava aika, koska se ei ole osa lauseketta, meillä on:

- t = x + 2

3. Korvaamme selvityksen ja pysymme:

- y = 2 (x + 2)

4. Sulujen ratkaiseminen, meillä on toisen yksikkövektorin tuloksena olevan etenemissuunnan yhtälö:

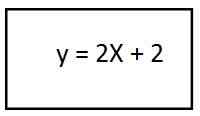
Tässä toimenpiteessä tulimme linjaan, joka kertoo meille, että suuntauksella on suorakulmainen muoto.

Ymmärtää siirtymä- ja etenemissuunnitelmat voimme päätellä muut erot, jotka ovat molempien termien välillä.

Lisää eroja siirtymisen ja radan välillä

Siirtymä

- Se on etäisyys ja suunta, jota objekti on kulunut ottaen huomioon sen alkuperäisen sijainti ja lopullinen sijainti.

- Tapahtuu aina suorassa linjassa.

- Tunnustetaan nuolella.

- Käytä pituusmittauksia (senttimetri, mittari, kilometri).

- Se on vektorisäki.

- Ota huomioon kulkenut suunta (oikea tai vasen)

- Ei pidä kiertueen aikana vietettyä aikaa.

Voi palvella sinua: Kondensaatio: Konsepti, prosessi, esimerkit

- Se ei riipu vertailujärjestelmästä.

- Kun lähtökohta on sama lähtökohta, siirtymä on nolla.

- Moduulin on oltava samanaikaisesti kiertueen tilan kanssa niin kauan kuin suuntaus on suora, eikä sitä seuraa muutoksia.

- Moduulilla on taipumus lisätä tai vähentää liikkeen tapahtuessa ottaen huomioon suuntaus.

Suunta

Se on objektin määrittelemä reitti tai linja sen liikkeen aikana. Hyväksy geometriset muodot (suora, parabolinen, pyöreä tai elliptinen).

- Sitä esitetään kuvitteellisen linjan kautta.

- Se mitataan metreinä.

- Se on skalaarinen määrä.

- Ei ota huomioon matkustettaessa.

- Harkitse kiertueen aikana vietettyä aikaa.

- Se riippuu viitejärjestelmästä.

- Kun lähtökohta tai alkupaikka on sama kuin lopullinen sijainti, suuntaus annetaan kulkevalla etäisyydellä.

- Siirtokauden arvo osuu samaan aikaan vektorin siirtymän moduulin kanssa, jos tuloksena oleva suuntaus on suora viiva, mutta seuraavissa mielessä ei ole muutoksia.

- Se kasvaa aina, kun vartalo liikkuu, radasta riippumatta.

Viitteet

1. Fernández, m., Fidalgo, j. (2016). Fysiikka ja kemia 1. ylioppilastutkinto. Paraninfo Editions, S.-Lla. Espanja.
2. Guatemalan radiokoulutuksen instituutti (2011) perusfysiikka. Ensimmäisen lukukauden Zaculeu -ryhmä. Guatemala.