Balacket -kolmion ominaisuudet, ominaisuudet, kaavat, alue

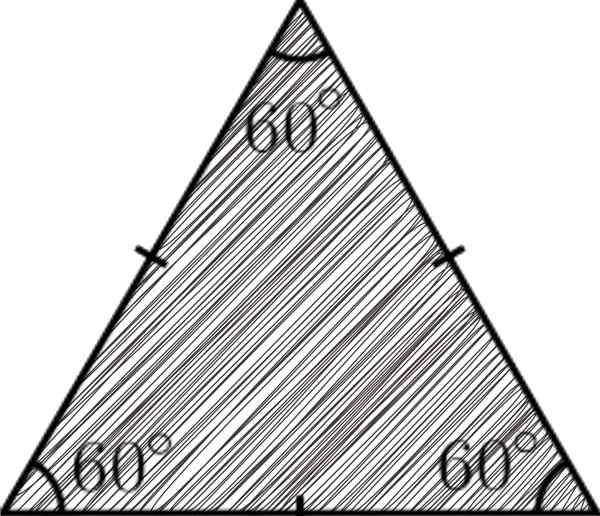
Eräs tasasivuinen kolmio Se on kolmipuolinen monikulmio, jossa kaikki ovat samoja; eli heillä on sama mitta. Tälle ominaisuudelle sille annettiin tasapainon nimi (yhtäläiset puolet).

Kolmiot ovat monikulmioita, joita pidetään geometrian yksinkertaisimpana, koska muodostetaan kolme puolta, kolme kulmaa ja kolme kärkeä. Tasasivuisen kolmion tapauksessa yhtä suuret puolet se tarkoittaa, että sen kolme kulmaa on myös.

Esimerkki tasapainosta kolmiosta

[TOC]

Tasapainomuotojen ominaisuudet

- Yhtäläiset puolet

Tasasivuiset kolmiot ovat tasaisia ​​ja suljettuja lukuja, jotka koostuvat kolmesta viivan linjasta. Kolmiot luokitellaan niiden ominaisuuksien mukaan suhteessa niiden sivuihin ja kulmiin; Tasasivuinen luokitella.

Tasasivuinen kolmio on erityinen tapausosaskisten kolmion tapaus, koska kaksi sen sivua on yhdenmukainen. Siksi kaikki tasaperusteiset kolmiot ovat myös tasa -arvoisia, mutta kaikki tasa -arvoiset kolmiot eivät ole tasa -arvoisia.

Tällä tavoin tasasivuisilla kolmioilla on samat ominaisuudet tasavirta kolmiosta.

Tassivuiset kolmiot voidaan myös luokitella niiden sisäisten kulmien amplitudilla tasapainon akuutiksi kolmioksi, jolla on kaikki kolme puolta ja kolme sisäkulmaa samalla tavalla. Kulmat ovat akuutteja, ts. Ne ovat alle 90^jompikumpi.

- Komponentit

Kolmioilla on yleensä useita linjoja ja pisteitä, jotka muodostavat sen. Niitä käytetään laskemaan pinta -ala, sivut, kulmat, mediaani, puolustaja, mediatrix ja korkeus.

• Mediaani: Se on linja, joka lähtee keskipisteestä toiselta puolelta ja saavuttaa vastakkaisen kärjen. Kolme väliainetta osallistuvat pisteeseen nimeltä Baricentro tai Centroid.
• Puolustaja: Se on puoliksi oikea, joka jakaa kärjen kulman kahteen yhtä suureen kulmaan, joten se tunnetaan symmetrian akselina. Tasasivuisella kolmiolla on kolme symmetria -akselia. Tasasivuisessa kolmiossa BISECTOR on piirretty kulman kärjen kärjestä vastakkaiselle puolelle, leikkaamalla sen keskipisteeseen. Olet kohta nimeltään kannustin.
• Mediatrix: Se on segmentti, joka on kohtisuorassa tämän keskeltä peräisin olevan kolmion sivulle. Kolmiossa on kolme mediaatiaa ja ne ovat yhtä mieltä kohdasta, jota kutsutaan Ympyräkeskukseksi.
• Korkeus: Se on linja, joka kulkee vastapäätä olevasta kärjestä ja myös tämä viiva on kohtisuorassa siihen puoleen. Kaikilla kolmioilla on kolme korkeutta, jotka ovat samat pisteet nimeltä Ortotenter.

Seuraavassa kaaviossa havaitsemme Scallene -kolmiota, jossa jotkut edellä mainituista komponenteista ovat yksityiskohtaisia

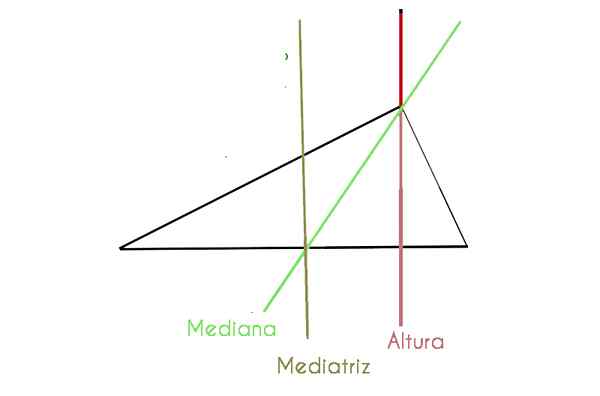Voimme nähdä komponentit selvästi, mikä on vaikeampaa tasapainossa kolmiossa, koska jotkut vastaavat. Selitämme ne alla:

Pakoitsija, mediaani ja mediatrix ovat sattumaa

Puolija jakaa kolmion viereen kahteen osaan. Tassivuisessa kolmioissa tämä puoli jaetaan kahteen täsmälleen samaan osaan, ts. Kolmio jaetaan kahteen yhdenmukaiseen suorakulmion kolmioon.

Siten tasavertaisen kolmion kulmasta vedetty puolustaja vastaa vastakkaisella puolella olevaa mediaania ja mediatrixiä kuin kyseinen kulma.

Voi palvella sinua: Suhteellisuussuhteet: Konsepti, esimerkit ja harjoitukset

Esimerkki:

Seuraava kuva näyttää ABC -kolmion keskimmäisellä D: llä, joka jakaa yhden sen sivuista kahteen AD- ja BD -segmenttiin.

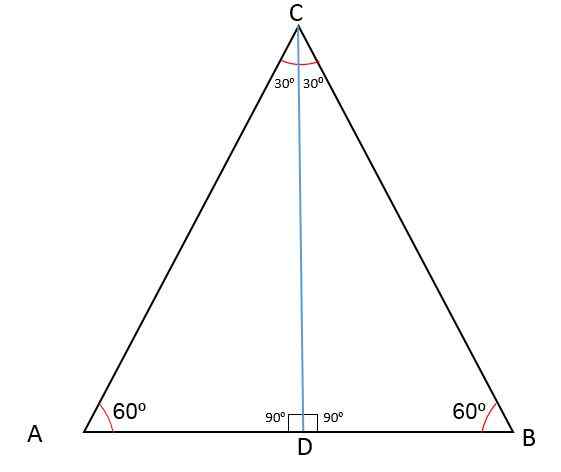
Kun piirtät viivan pisteestä D vastakkaiseen kärkeen, saadaan määritelmän mukaan mediaani CD, joka on suhteessa kärkeen C ja sivuun AB.

Kun CD -segmentti jakaa ABC -kolmion kahteen yhtä suureen CDB- ja CDA -kolmioon, se tarkoittaa, että kyseessä on kongruenssi: sivu, kulma, puoli ja siksi CD ovat myös BCD BISECtor.

Piirrät CD -segmenttiä, kärjen kulma on jaettu kahteen yhtä suureen kulmaan 30^jompikumpi, Vertex A: n kulma mittaa edelleen 60^jompikumpi Ja CD -viiva muodostaa 90 kulman^jompikumpi Keskipisteen d.

CD -segmentti muodostaa kulmat, joilla on sama mitta ADC- ja BDC -kolmioille, ts. Ne ovat täydentäviä siten, että kunkin mitta on:

Lääketieteellinen. (Adb) + med. (ADC) = 180^jompikumpi

2 _* Lääketieteellinen. (ADC) = 180^jompikumpi

Lääketieteellinen. (ADC) = 180^jompikumpi ÷ 2

Lääketieteellinen. (ADC) = 90^jompikumpi.

Ja niin, CD -segmentti on myös Mediatrix AB -puolella.

Puoli ja korkeus ovat sattumaa

Kun puolustaja jäljittää kulman kärkipaikasta vastakkaisen puolen keskipisteeseen, tämä jakaa tasapainon kolmion kahteen yhdenmukaiseen kolmioon.

Siten, että 90 kulma muodostuu^jompikumpi (suoraan). Tämä osoittaa, että tämä linjasegmentti on täysin kohtisuorassa siihen puoleen nähden, ja määritelmän mukaan tämä viiva olisi korkeus.

Tällä tavoin tasapainon kolmion kulman puolustaja on samaan aikaan kuin korkeus suhteessa kyseisen kulman vastakkaiseen puoleen.

Orocentro-, Baricentro-, Incentro- ja Colecentro -kolinsidit

Kun korkeus, mediaani, puolustaja ja mediatrix ovat saman segmentin edustettuna samanaikaisesti näiden segmenttien kokouspisteiden -ortokeskuksen, baricenterin, kannustuksen ja ympärileikkauksen -kokouspisteissä -samassa vaiheessa:

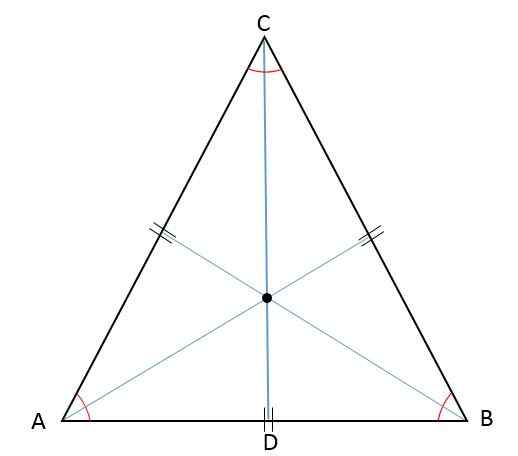
Ominaisuudet

Tasasivuisten kolmioiden pääominaisuus on, että ne ovat aina tasapelin kolmiot, koska samoitusmuodot muodostavat kaksi yhdenmukaista puolta ja tasapainot kolmella.

Tällä tavoin tasapainoskolmiot perivät kaikki Basosceles -kolmion ominaisuudet:

Sisäkulmat

Sisäisten kulmien summa on aina yhtä suuri kuin 180^jompikumpi, Ja koska kaikki sen kulmat ovat yhdenmukaisia, niin jokainen näistä mittaa 60^jompikumpi.

Ulkokulmat

Ulkoisten kulmien summa on aina yhtä suuri kuin 360^jompikumpi, Siksi jokainen ulkoinen kulma mittaa 120^jompikumpi. Tämä johtuu siitä, että sisäiset ja ulkoiset kulmat ovat täydentäviä, ts. Lisäämällä ne ovat aina yhtä suuret kuin 180^jompikumpi.

Sivujen summa

Kahden osapuolen mittojen summan on aina oltava suurempi kuin kolmannen puolen mitta, ts. A + B> C, missä a, b ja c ovat mittaukset molemmilla puolilla.

Yhtenäiset osapuolet

Tasasivuisella kolmioilla on kolme sivua samalla mittalla tai pituudella; eli he ovat yhdenmukaisia. Siksi edellisessä tuotteessa sinun on = b = c.

Yhdenmukaiset kulmat

Tassivuiset kolmiot tunnetaan myös nimellä tasa -arvoinen kolmio, koska niiden kolme sisäkulmaa ovat yhdenmukaisia ​​keskenään. Tämä johtuu siitä, että kaikilla heidän puolillaan on myös sama mitta.

Se voi palvella sinua: Nimellinen muuttuja: Konsepti ja esimerkit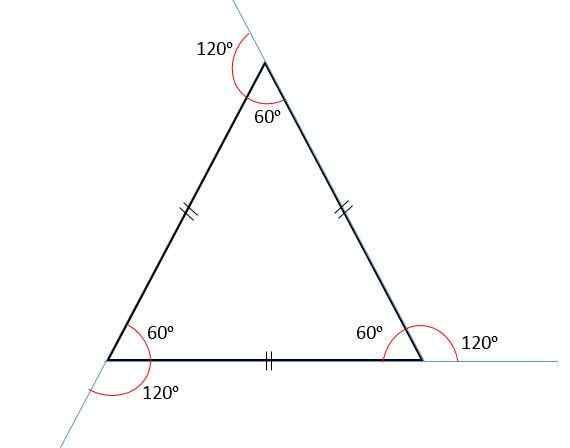

Kuinka kehä lasketaan?

Polygonin kehä lasketaan sivujen summan perusteella. Kuten tässä tapauksessa tasapainoskolmiolla on kaikki sivunsa samalla mittauksella, sen kehä lasketaan seuraavalla kaavalla:

P = 3 _* sivu-.

Kuinka laskea korkeus?

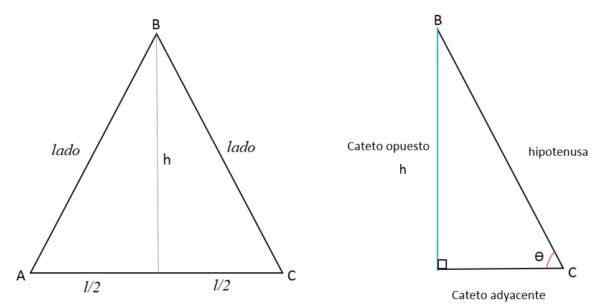
Koska korkeus on pohjaan kohtisuorassa oleva viiva, jaa se kahteen yhtä suureen osaan ulottumalla vastakkaiseen kärkeen. Siten kaksi kolmiota muodostetaan yhtä suuret suorakulmiot.

Korkeus (H) edustaa vastakkaista katetoa (A), puolet vaihtovirtapuolesta viereiselle katetolle (b) ja BC -puoli edustaa hypotenusia (c).

Käyttämällä Pythagoras -lausetta, korkeuden arvo voidaan määrittää:

-lla² + b -² = c²

Missä:

-lla² = korkeus (h).

b -² = sivu B / 2.

c² = puoli a.

Näiden arvojen korvaaminen Pythagoras -lauseessa ja puhdistamalla korkeus:

h² + ( l / l / 2)² = lens²

h² +  lens²- 4 = lens²

h² = lens²  -  lens²- 4

h² = (4_*lens² -  lens²-A - 4

h² =  3_*lens² -4

√h² = √ (3_*lens² -4)

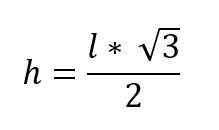
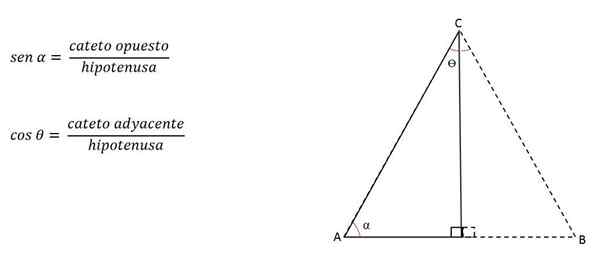
Jos yhtenäisten puolten muodostama kulma, korkeus (jalan edustama) tunnetaan, se voidaan laskea soveltamalla trigonometrisiä syitä.

Luokkia kutsutaan päinvastaiseksi tai vierekkäin kulmasta riippuen, jota pidetään viitteenä.

Esimerkiksi edellisessä kuvassa Cateto H on vastapäätä kulmalle C, mutta kulman B vieressä:

Siten korkeus voidaan laskea:

Kuinka laskea sivut?

On tapauksia, joissa kolmion sivujen mittauksia ei tunneta, vaan sen korkeus ja kärjessä muodostuvat kulmat.

Alueen määrittämiseksi näissä tapauksissa on tarpeen soveltaa trigonometrisiä syitä.

Tietäen yhden sen kärkipisteiden kulman, luokka tunnistetaan ja käytetään vastaavaa trigonometristä syytä:

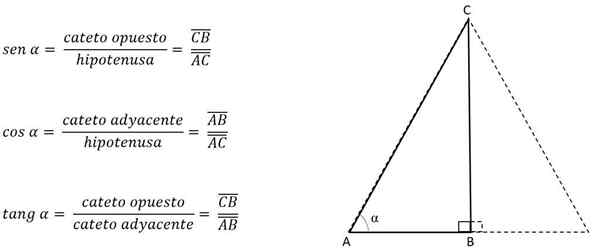
Siten Cateto AB vastustaa kulmaa C, mutta kulman a vieressä. Korkeutta vastaavasta sivusta tai jalasta riippuen toinen puoli puhdistetaan tämän arvon saamiseksi, tietäen, että tasasivuisessa kolmiossa kolmella puolella on aina sama mitta.

Kuinka laskea alue?

Kolmiot lasketaan aina samalla kaavalla, kertomalla pohja korkeudella ja jakamalla kahdella:

Alue = (b _* H) ÷ 2

Tietäen, että korkeus antaa kaava:

Harjoitukset

- Ensimmäinen harjoitus

ABC: n tasapainon kolmion sivut mittaavat 20 cm. Laske sen monikulmion korkeus ja pinta -ala.

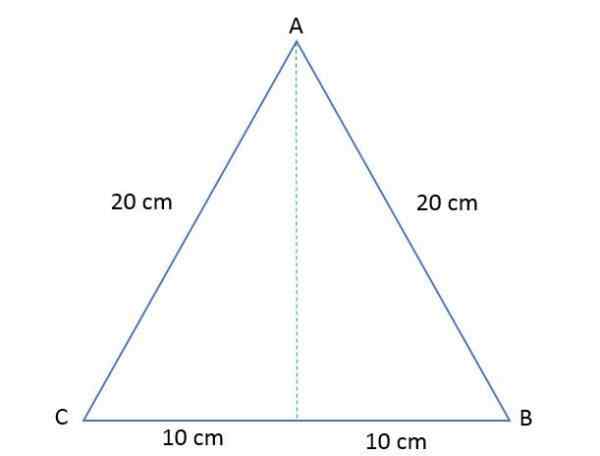
Ratkaisu

Tämän tasapainon kolmion pinta -alan määrittämiseksi on tarpeen laskea korkeus tietäen, että piirtäessäsi se jakaa kolmion kahteen yhtä suureen suorakulmioon.

Tällä tavalla voit käyttää Pythagoras -lausetta sen löytämiseen:

-lla² + b -² = c²

Missä:

A = 20/2 = 10 cm.

B = korkeus.

C = 20 cm.

Tiedot korvataan lauseessa:

10² + b -² = 20²

100 cm + b -² = 400 cm

b -² = (400 - 100) cm

b -² = 300 cm

B = √300 cm

B = 17,32 cm.

Toisin sanoen kolmion korkeus on yhtä suuri kuin 17,32 cm. Nyt on mahdollista laskea annettu kolmioalue korvaamalla kaava:

Alue = (b _* H) ÷ 2

Alue = (20 cm _* 17,32 cm) ÷ 2

Se voi palvella sinua: lineaariset muunnokset: Ominaisuudet, mitkä ovat käyttö, tyypit, esimerkit

Alue = 346,40 cm² ÷ 2

Alue = 173,20 cm².

Toinen yksinkertaisempi tapa ratkaista harjoitus on tietojen korvaaminen alueen suorassa kaavassa, jossa myös korkeuden arvo löytyy epäsuorasti:

- Toinen harjoitus

Pellossa, jolla on tasapainon kolmion muoto, kukat istuttavat. Jos kyseisen maaston kehä on yhtä suuri kuin 450 m, laske kukkia miehittävien metrien lukumäärä.

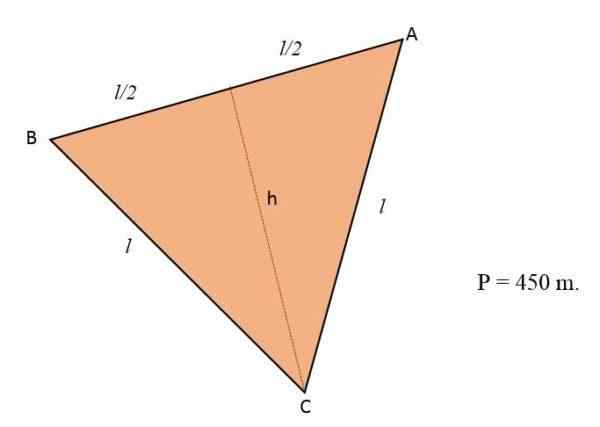
Ratkaisu

Tietäen, että kolmion kehä vastaa sen kolmen sivun summaa ja koska maasto on muotoiltu tasapainon kolmioksi, tämän kolmen puolen on sama mitta tai pituus:

P = sivu + puoli + puoli = 3 _* lens

3 _* lens = 450 m.

L = 450 m ÷ 3

L = 150 m.

Nyt on tarpeen laskea vain kyseisen kolmion korkeus.

Korkeus jakaa kolmion kahteen yhdenmukaiseen suorakulmioon kolmioon, joissa yksi luokista edustaa korkeutta ja pohjan toista puolta. Pythagoras -lauseen mukaan korkeus voidaan määrittää:

-lla² + b -² = c²

Missä:

-lla = 150 m ÷ 2 = 75 m.

c = 150 m.

b - = korkeus

Tiedot korvataan lauseessa:

(75 m)² + b -² = (150 m)²

5.625 m + b -² = 22.500 m

b -² = 22.500 m - 5.625 m

b -² = 16.875 m

b - = √16.875 m

b - = 129,90 m.

Siten alue, jonka kukat miehittävät, ovat:

Alue = B * H ÷ 2

Pinta -ala = (150 m _* 129,9 m) ÷ 2

Alue = (19.485 m²) ÷ 2

Alue = 9.742,5 m²

- Kolmas harjoitus

ABC: n tasa -arvoinen kolmio jaetaan linjasegmentillä, joka kulkee sen kärkipisteestä C -puolivälille D, joka sijaitsee vastakkaisella puolella (AB). Tämä segmentti mittaa 62 metriä. Laske tämän tasapainon kolmion pinta -ala ja kehä.

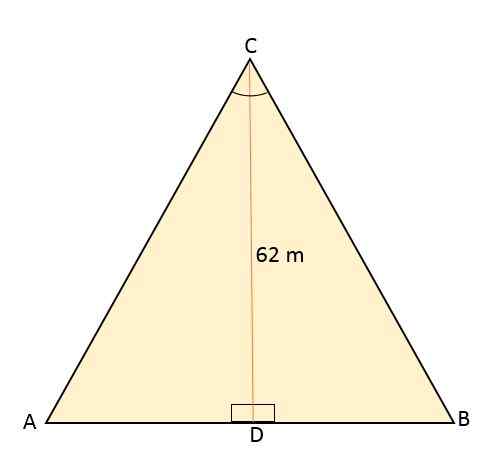
Ratkaisu

Tietäen, että tasasivuinen kolmio on jaettu linjasegmentillä, joka vastaa korkeutta, muodostaen siten kaksi yhdenmukaista suorakulmiota, tämä puolestaan ​​jakaa myös kärjen C -kulman kahteen kulmaan, jolla on sama mitta, 30, 30^jompikumpi jokainen.

Korkeus muodostaa 90 kulman^jompikumpi Segmentin AB: n ja kärjen kulman suhteen mitataan sitten 60^jompikumpi.

Sitten käyttämällä 30 kulmaa referenssinä^jompikumpi, CD.

Näistä tiedoista voidaan määrittää yhden kolmion sivun arvo trigonometrisiä syitä käyttämällä:

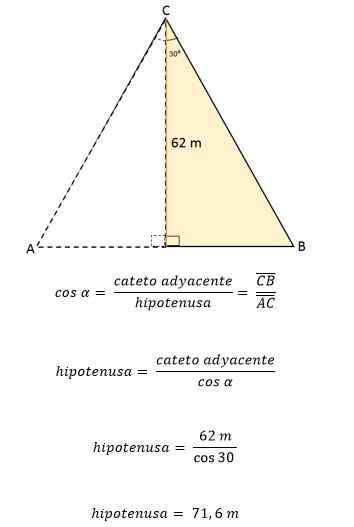
Kuten tasapainon kolmiossa, kaikilla puolilla on täsmälleen sama mitta tai pituus, se tarkoittaa, että ABC: n tasapainon kolmion molemmat puolet ovat yhtä suuret kuin 71,6 metriä. Tietäen sen, on mahdollista määrittää alueesi:

Alue = B * H ÷ 2

Alue = (71,6 m _* 62 m) ÷ 2

Alue = 4.438,6 m² ÷ 2

Alue = 2.219,3 m²

Kehä annetaan sen kolmen puolen summalla:

P = sivu + puoli + puoli = 3 _* lens

P = 3_*lens

P = 3 _* 71,6 m

P = 214,8 m.

Viitteet

1. Álvaro Rendón,. R -. (2004). Tekninen piirustus: Aktiviteettikirja.
2. Arthur Goodman, L. H. ( 1996). Algebra ja trigonometria analyyttisellä geometrialla. Pearson -koulutus.
3. Baldor, a. (1941). Algebra. Havana: Kulttuuri.
4. Barbosa, J. Lens. (2006). Litteä euklidinen geometria. SBM. Rio de Janeiro, .
5. Coxford, a. (1971). Geometria muutosmenetelmä. USA: Laidlaw Brothers.
6. Euklidi, r. P. (1886). Euclidin geometrian elementit.
7. Héctor Trejo, J. S. (2006). Geometria ja trigonometria.
8. León Fernández, G. S. (2007). Integroitu geometria. Metropolitan Technological Institute.
9. Sullivan, J. (2006). Algebra ja trigonometria. Pearson -koulutus.