Teselados -ominaisuus, tyypit (säännöllinen, epäsäännöllinen), esimerkkejä

Se Hölynpölyinen Ne ovat pintoja, jotka on peitetty yhdellä tai useammalla nimeltään hahmo Tesselit. Ne ovat kaikkialla: kaikenlaisissa kaduissa ja rakennuksissa. Tesselit tai laatat ovat litteitä kappaleita, yleensä monikulmioita, joissa on yhdenmukaisia ​​tai isometrisiä kopioita, jotka asetetaan säännöllisen kuvion jälkeen. Tällä tavoin ei ole tiloja ilman peittämistä, ja laatat tai mosaiikit eivät ole päällekkäisiä. 

Jos käytetään yhden tyyppistä mosaiikkityyppistä mosaiikkia säännöllinen tesseld, Mutta jos käytetään kahta tai useampaa tyyppiä tavallisia monikulmioita, niin se on Puoliksi säädetty.

Kuvio 1. Epäsäännölliset laattalattialattia, koska suorakulmiot ovat ei-säännöllisiä monikulmioita, vaikka neliöt ovat. Lähde: Pixabay.

Lopuksi, kun Tesseldon muodostavat monikulmiot eivät ole säännöllisiä, joten se on a epäsäännöllinen.

Yleisin Tesseldo -tyyppi on suorakaiteen muotoinen ja erityisesti neliömäinen mosaiikki. Kuvassa 1 meillä on hyvä esimerkki.

[TOC]

Teseladojen historia

Tessellaatiota on käytetty tuhansien vuosien ajan kattamaan eri kulttuurien ja uskontojen palatsien ja temppelien lattiat ja seinät.

Esimerkiksi Sumerian sivilisaatio, joka kukoisti noin 3500.C. Eufrates- ja Tigris Riversin välissä Mesopotamiasta eteläpuolella he käyttivät arkkitehtuurissa olevia keskuksia.

Kuva 2. Teselados Sumerios ISTARin ovella. Lähde: Wikimedia Commons.

Teselit ovat myös herättäneet kaikkien aikojen matemaatikkojen kiinnostuksen: alkaen Archimedesistä kolmannella vuosisadalla eKr.

Se voi palvella sinua: fraktio vastaa 3/5 (ratkaisu ja selitys)

Penrose loi ei -periodisen tessellation, joka tunnetaan nimellä Penrose Tessellation. JAnämä Ne ovat vain joitain tutkijoiden nimiä, jotka ovat vaikuttaneet paljon Tessellationista.

Tavalliset kesteet

Säännöllinen teslate on valmistettu yhden tyyppisellä tavallisella monikulmiolla. Toisaalta, jotta Tesseldoa voidaan pitää säännöllisenä koko koneen pisteen on:

-Kuulua monikulmioon

-Tai kahden vierekkäisen monikulmion reunaan 

-Lopuksi se voi kuulua vähintään kolmen monikulmion yleiseen kärkeen.

Edellä olevien rajoitusten avulla voidaan osoittaa, että vain tasapainon kolmiot, neliöt ja kuusikulmiot voivat muodostaa säännöllisen tesselin.

Nimikkeistö

Teselit, jotka koostuvat listautumisesta kellon neulojen suuntaan, on nimikkeistö, joka on erotettu pisteellä, tesseledin jokaista solmu (tai kärkipaikan) sivujen lukumäärää, aina alkaen pienimmällä numerolla. puolet.

Tämä nimikkeistö koskee säännöllisiä ja puoliarjoajia. 

Esimerkki 1: Kolmion teselado

Kuvio 3 esittää kolmion säännöllisen laatan. On huomattava, että jokainen kolmion muotoinen laattasolmu on kuuden tasapainon kolmion yleinen kärki. 

Tapa osoittaa tämän tyyppistä Tesseldoa on 3.3.3.3.3.3, jota merkitään myös 3⁶.

Kuva 3. Kolmion säännöllinen Teselado 3.3.3.3.3.3. Lähde: Wikimedia Commons

Esimerkki 2: Square Tessel

Kuvio 4 esittää tavallisen laatan, joka koostuu vain neliöistä. On huomattava, että jokaista laattasolmua ympäröi neljä yhdenmukaista neliötä. Tämän tyyppisiin neliömäisiin tiloihin liittyvä merkintä on: 4.4.4.4 o vuorotellen 4⁴

Kuva 4. Square Tesseld 4.4.4.4. Lähde: Wikimedia Commons.

Esimerkki 3: Hexagonal Tesseld

Kuusikulmainen Tesselle. Tavallisen kuusikulmaisen tilojen nimikkeistö on 6.6.6 o vuorotellen 6³.

Voi palvella sinua: Kartiomaiset osat: Tyypit, sovellukset, esimerkit Kuva 5. Kuusikulmainen Tesseld 6.6.6. Lähde: Wikimedia Commons.

Puoliksi säädetty

Archimedesin puoliksi säännölliset tai tessellisoidut kesteet koostuu kahdesta tai useammasta tavallisesta monikulmiosta. Jokaista solmua ympäröivät tyypit monikulmiot, jotka muodostavat tesselloituneen samassa järjestyksessä, ja naapurin kanssa täysin jaetun reunan kunto ylläpidetään.

Kahdeksan puoliarjoaja keskiasteita on:

1. 3.6.3.6 (tri-heksagonaalinen tesselled)
2. 3.3.3.3.6 (kuusikulmainen teslate romo)
3. 3.3.3.4.4 (Elongado -kolmionmuotoinen Teselado)
4. 3.3.4.3.4 (Romo Square Tesselled)
5. 3.4.6.4 (ROMBI-TRI-HECAGANAL TESSELD)
6. 4.8.8 (katkaistu neliömäinen)
7. 3.12.12 (katkaistu kuusikulmainen Tesseld)
8. 4.6.12 (katkaistu tri-heksagonaalinen Tesseld)

Joitakin esimerkkejä puoliarjouksesta Teslate on esitetty alla.

Esimerkki 4: Tixagonal Teselado

Se koostuu tavallisista tasapaino kolmioista rakenteessa 3.6.3.6, mikä tarkoittaa, että ympäröi laattasolmu (kunnes se täydentää paluuta) kolmion, kuusikulmion, kolmion ja kuusikulmion kautta. Kuvio 6 esittää sellaisen Tesselin.

Kuva 6. Tri-heksagonaalinen Tesseld (3.6.3.6) Se on esimerkki puoliarjouksesta. Lähde: Wikimedia Commons.

Esimerkki 5: Hexagonal Tesseldo Romo

Kuten edellisen esimerkin laatta, tämä koostuu myös kolmioista ja kuusikulmioista, mutta sen jakautuminen solmun ympärillä on 3.3.3.3.6. Kuvio 7 havainnollistaa selvästi tämän tyyppistä tipistettyjä.

Kuva 7. Kuusikulmainen Tesseldo Romo koostuu kuusikulmiosta, jota ympäröi 16 kolmiota kokoonpanossa 3.3.3.3.6. Lähde: Wikimedia Commons.

Esimerkki 6: Rombi-tri-heksagonaalinen Tessel

Se on laatta, joka koostuu kolmioista, neliöistä ja kuusikulmioista, kokoonpanossa 3.4.6.4, joka on esitetty kuvassa 8.

Kuva 8. Puoli -säännöllinen tipistetty koostuva kolmiosta, neliöstä ja kuusikulmiosta konfiguraatiossa 3.4.6.4. Lähde: Wikimedia Commons.

Epäsäännölliset kesteet

Niitä kutsutaan epäsäännöllisiksi kestäviksi niille, jotka muodostavat epäsäännölliset monikulmiot tai tavalliset monikulmiot, mutta jotka eivät täytä kriteeriä, että solmu on vähintään kolmen monikulmion kärkipiste.

Se voi palvella sinua: Antidervative: Kaavat ja yhtälöt, esimerkit, harjoitukset

Esimerkki 7

Kuvio 9 esittää esimerkkiä epäsäännöllisestä laattasta, jossa kaikki monikulmiot ovat säännöllisiä ja yhteneviä. Se on epäsäännöllinen, koska solmu ei ole ainakin kolmen neliön yleinen kärki, ja on myös naapurialueita, jotka eivät jaka kokonaan reunaa.

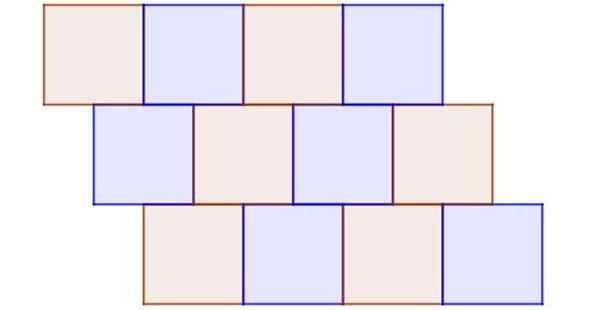Kuva 9. Jopa silloin, kun kaikki laatat ovat yhtenäisiä neliöitä, tämä on selkeä esimerkki epäsäännöllisestä tiputtamisesta. Lähde: f. Zapata.

Esimerkki 8

Rinnakkaisogrammit ovat tasaisen pinnan, mutta ellei neliö ei voi muodostaa tavallista tiputta.

Kuva 10. Rinnakkaisogrammien muodostama Tesseldo on epäsäännöllinen, koska sen mosaiikit ovat ei -sääntöjen monikulmioita. Lähde: f. Zapata.

Esimerkki 9

Ei-säännölliset kuusikulmiot keskussymmetrialla asettavat tasaisen pinnan, kuten seuraavassa kuvassa esitetään:

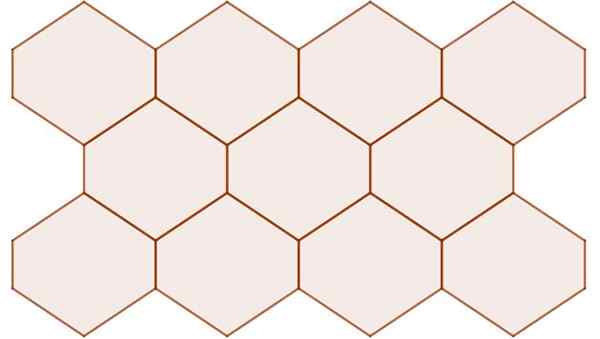Kuva 11. Hexagonit keskussymmetrialla, vaikka he eivät ole säännöllisiä, he asettavat lentokoneen. Lähde: f. Zapata.

Esimerkki 10: El Kairo Teselado

Se on erittäin mielenkiintoinen tessellaatio, joka koostuu pentagoneista, joiden sivut ovat yhtä pituisia, mutta epätasa -arvoisilla kulmilla, joista kaksi ovat suorat ja kolmen muun 120º.

Hänen nimensä tulee, että tämä Tesseld on joidenkin Egyptin Kairon kadujen jalkakäytävä. Kuvio 12 esittää Kairon Tesseldon.

Kuva 12. Kairo Tesseldo. Lähde: Wikimedia Commons.

Esimerkki 11: Teselado al-Andalus

Tesseldolla tietyissä Andalusian ja Pohjois -Afrikan osissa on ominaista geometria ja epigrafia koristeellisten elementtien, kuten kasvillisuuden, lisäksi. 

Palacios's Tesselled, kuten Alhambra, joka koostuu monien värien keraamisten kappaleiden muodostuneista laattoista, joissa on useita (ei äärettömiä) muotoja, jotka laukaisivat geometriset kuvaajat.

Kuva 13. Teselado Palacio de la Alhambra. Tartaglia / julkinen alue

Esimerkki 12: Teselado videossa

Se tunnetaan myös nimellä Tesellation, se on yksi videopelien puomista. Tämä on tekstuurien luominen simulaattorissa näkyvien erilaisten skenaarioiden simuloimiseksi.

Tämä on selvä heijastus, että nämä kannet kehittyvät edelleen siirtämällä todellisuuden rajat.

Viitteet

1. Nauti matematiikasta. Kiput. Toipunut.com
2. Rumiñot. Teselit ratkaisivat esimerkkejä. Toipunut: matematiikka.Blogin.com
3. Weisstein, Eric W. "Deiregula Tessellation". Weisstein, Eric W, Ed. Matematiikka. Wolfram -tutkimus.
4. Wikipedia. Hölynpölyinen. Palautettu: on.Wikipedia.com
5. Wikipedia. Säännöllinen tesseld. Palautettu: on.Wikipedia.com