Järjestysmuuttuja

Mikä on ordinaali?

Ordinaalimuuttuja on sellainen, joka voidaan tilata (tai tarkoittaa tilausta). Esimerkiksi henkilön asemuuttuja voidaan luokitella: korkea, keskimääräinen ja alhainen.

Ordinaalisella asteikolla, joka on tunnistamisen, ryhmittelyn ja erottamisen ja erottamisen lisäksi nimellismuuttujana, kuvaa myös suuruutta, ja siten sille on ominaista tilaus; toisin sanoen tutkimusyksiköt voidaan tilata yhä enemmän tai vähenevästi suuruuden suhteen.

Tämä asteikko puhuu ensimmäisestä, toisesta, kolmannesta tai korkeasta, keskikokoisesta bassosta; Mutta mittaan ei ole vahvistettu luokkien välillä. Esimerkiksi: Muuttujan pätevyys tarjottujen palvelun tyytyväisyystestissä voidaan mitata neljään luokkaan: tyytymätön, välinpitämätön, tyytyväinen, erittäin tyytyväinen.

Se voidaan tilata ilmeisen tyytyväisyyden mukaan, mutta ei tiedetä kuinka erilainen.

Ordinaalisella asteikolla tarkoitetaan mittauksia, jotka tekevät vain "suuria", "vähäisiä" tai "yhtäläisiä" vertailuja peräkkäisten mittausten välillä. Edustaa havaitun arvojoukon luokittelua tai järjestystä.

Käsite ordinaalista ja ominaisuuksista

Ordinaalisessa mittakaavassa havainnot asetetaan suhteelliseen järjestykseen suhteessa ominaispiirteisiin, jotka on arvioitu. Eli tietokategoriat luokitellaan tai tilata.

Jos käytämme numeroita, näiden suuruus edustaa havaitun ominaisuuden alueen järjestystä. Vain suhteilla "suurempi kuin", "alempi kuin" ja "yhtä suuri kuin" on merkitys ordinaalisen mittausasteikolla.

Voi palvella sinua: euklidinen geometria

Matemaattisesta näkökulmasta ja kuten nimellisasteikot, ordinaaliset asteikot myöntävät vain mittasuhteiden, prosenttiosuuksien ja syiden laskemisen.

Keskeinen taipumusmitta, joka selittää parhaiten ordinaalin muuttujan, on mediaani, joka on arvo, joka sijaitsee tilatun tietojoukon keskellä vähiten suurimpaan.

Kun esineet luokitellaan ominaispiirteellä, on mahdollista selvittää, millä esineellä on enemmän tai vähemmän ominaispiirteitä toiseen verrattuna; Mutta eroa ei voida määrittää.

Esimerkiksi kolme objektia, jotka on tilattu 'ensimmäiseksi', 'toiseksi' ja 'kolmanneksi', ottaen huomioon kaikki ominaisuudet. Toinen paikka eroaa ensimmäisestä määrästä, joka ei välttämättä ole yhtä suuri kuin määrä, jossa se eroaa kolmannesta paikasta.

Esimerkkejä ordinaalista muuttujista

Joitakin esimerkkejä ordinaalista muuttujista:

- Sosiaalinen luokka (a - korkea; b - korkea media; c - media; d - matala; e - erittäin matala).

- Laadulliset koulutehtävät (i - riittämättömät; A - hyväksyttävä; B - hyvä; S - Erinomainen; E - Erinomainen).

- Sotilaalliset tutkinnot (kenraali, eversti, everstiluutnantti, majuri, kapteeni jne.-A.

- Koulututkinto (ala-, lukio, ammattiteknikko, teknikko, yliopisto jne.-A.

- Ihmisen kehitysvaihe (vastasyntynyt, vauva, lapsi, nuori, aikuinen, vanha).

- Elokuvien luokittelu (A - kaikki yleisöt; b - yli 12 vuotta; c - yli 18 vuotta; D - yli 21 vuotta).

- Hedelmän kypsyys (vihreä, maali, kypsä, erittäin kypsä, mätä).

- Tyytyväisyys julkisen palvelun tarjoamiseen. (Erittäin tyytyväinen; tyytyväinen; välinpitämätön; jne jne.-A.

Voi palvella sinua: Ryhmätiedot: Esimerkit ja liikunta ratkaistu

- Selitetty esimerkkejä

Hänen oppilaidensa opettajan arviointi

Tietyn kurssin opiskelijoilla on mahdollisuus täyttää kysely opettajansa pedagogisen kapasiteetin arvioimiseksi, joka mitataan ordinaalisella muuttujalla, jonka asteikko on: 5 - erinomainen, 4 - kaivo, 3 - keskimäärin 2 - huono, 1 - 1 - huono.

Muuttujan arvot on järjestetty suuremmasta tai paremmasta vähemmän tai huonompaan: erinomainen on parempi kuin hyvä, se on keskimääräistä parempi jne. Erojen suuruutta ei kuitenkaan ole mahdollista erottaa.

On ero erinomaisen ja hyvän välillä? Sitä ei ole mahdollista vahvistaa.

Jos käytämme numeroita, nämä eivät tarkoita suuruutta. Esimerkiksi, ei pidä päätellä, että hyvä pätevyys (pätevyys 4) on kaksi kertaa korkeampi kuin huono (pätevyys 2). Voidaan vain sanoa, että hyvä pätevyys on parempi kuin huono luokitus, mutta sitä ei voida määrittää missä määrin se on parempi.

Aterian hyväksymisaste

Maistamiskilpailu arvioi aterioita keittiökilpailussa ordinaalin muuttujan kautta hyväksymisellä: A - Erinomainen, B - No, C - ei hyväksyttävä. Osallistuvan mittauksen käyttöä alhaisimmasta on osoitettu, mutta asteikon arvojen välistä eroa ei ole mahdollista määrittää.

Koska se on kilpailu, kuinka voittaja määritetään? Vaikuttaa siltä, ​​että sopivin on muodin käyttö päätöksen tekemiseen kilpailun voittajasta. Ymmärrä muotina nimellä, joka on annettu suurimmalle arvolle (yleisimmin) tasoa kohti. Esimerkiksi 5 a, 14 b, 10 ° C laskettiin; Muoti on B, koska se on taso, jolla oli eniten mielipiteitä.

Voi palvella sinua: Logaritminen funktio: Ominaisuudet, esimerkit, harjoitukset

Erot nimellismuuttujan kanssa

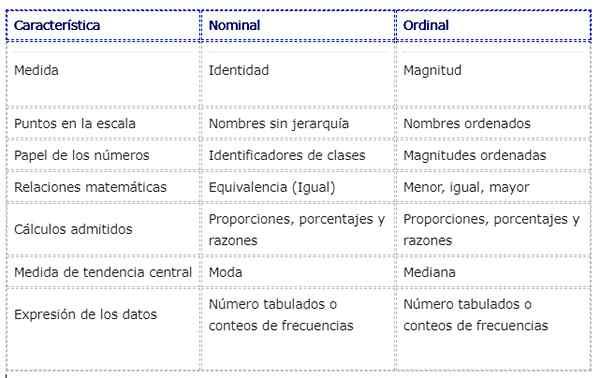
Seuraava taulukko näyttää joitain eroja ja yhtäläisyyksiä nimellisessä ja ordinaalisessa mittakaavassa mitattujen muuttujien välillä:

Viitteet

1. Freund, r.; Wilson, W.; Mohr, D. (2010). Tilastolliset menetelmät. Kolmas Ed. Akateeminen lehdistösekki Inc.
2. Lasi, G.; Stanley, J. (1996). Tilastolliset menetelmät, joita ei sovelleta yhteiskuntatieteisiin. Hispanoamerican Hall Hall s. -Lla.
3. Kaunis.; Marchal, W.; Wathen, S. (2012). Tilastot sovelletaan liiketoimintaan ja talouteen. Kymmenes ED. McGraw-Hill/Amerikanväliset toimittajat S. -Lla.
4. Orlandoni, G. (2010). Tilastolliset mittausasteikot. Telos -aikakauslehti. Haettu OJ: stä.kaupunki.Edu.
5. Siegel, S.; Castellan, n. (1998). Käyttäytymistieteisiin sovelletut ei -parametriset tilastot. Neljäs Ed. Toimituksellinen trillas S. -Lla.
6. Wikipedia. (2019). Mittaustaso. Haettu jstk.Wikipedia.org.