Mikä on suhteellinen taajuus ja miten se lasketaan?

Tilastollinen taajuus viittaa tapahtuman tai tapahtuman toistoon, kun taas suhteellinen taajuus Se viittaa vertailuun; Toisin sanoen suhteellisen taajuuden puhuminen on selvittää, kuinka paljon tapahtuma toistetaan suhteessa mahdollisiin tapahtumiin.

Esimerkiksi tietyn ikäisten lasten lukumäärä suhteessa koulun lasten kokonaismäärään tai kuinka monta urheiluajoneuvoa on kaikissa parkkipaikan ajoneuvoissa.

Tiedonhallinnan yhteydessä on joskus kätevää luokitella ne joidenkin ominaisuuksien mukaan, esimerkiksi väestölaskentatiedot voidaan ryhmitellä ikäryhmien, tulotason, koulutustason jne.

Näitä ryhmiä kutsutaan luokkiin ja kutakin luokkaa vastaavien elementtien määrää kutsutaan luokkataajuudeksi tai absoluuttiseksi. Kun taajuus on jaettu datan kokonaismäärän välillä, alikvootti saadaan.

Alikvootti edustaa kyseistä luokkaa suhteessa kokonaismäärään ja tunnetaan suhteellisena taajuutena, joka ilmaistaan ​​määränä nollan ja yhden välillä tai kerrotaan prosenttiosuutena ja ilmaistaan ​​prosentteina kokonaismäärästä.

Esimerkiksi, jos sinulla on 20 7 -vuotiaita lapsia koulun pihalla, jossa on 100 lasta; Suhteellinen taajuus olisi 20/100 = 0.2 tai 20%.

Taajuuspöydät

Suhteellinen taajuus on yksi niistä elementeistä, jotka muodostavat taajuusjakaumataulukon. Nämä taulukot esittävät tietoryhmän sisältämät tiedot, jotka luokkien tilaavat tietyn ominaisuuden suhteen.

Rakentamisensa vuoksi luokkien lukumäärä on määritettävä, näiden rajat (joiden on oltava selkeitä ja yksinoikeuksia), luokan edustava arvo ja taajuudet.

Voi palvella sinua: Täydentävät kulmat: mitkä ja miten ne lasketaan, esimerkkejä, harjoituksia

Variaation amplitudi: Ero vanhempien ja vähiten lukujen välillä.

Luokkien lukumäärä: luokkien lukumäärä, joista jaamme numerot. Se on yleensä välillä 5 - 20.

Luokkaväli: luokan määrittelevien arvojen aikaväli. Sen päätä kutsutaan ala- ja ylärajoiksi.

Luokan tuotemerkki (XI): Luokan väli- tai luokan edustaja -arvo. Teoriassa oletetaan, että kaikki luokan arvot osuvat tämän määrän kanssa.

Suhteellinen taajuuslaskenta

Aiomme rakentaa taajuuden jakautustaulukon esimerkiksi, ja sen kanssa havainnollistamme, kuinka suhteellinen taajuus lasketaan.

Otetaan Canavosista, 1998, seuraava tapaustutkimus:

Haluat tietää P & R -yhtiön työntekijöiden viikoittaisen palkan.S. $. Tätä varten valitaan edustava näyte 65 työntekijästä.

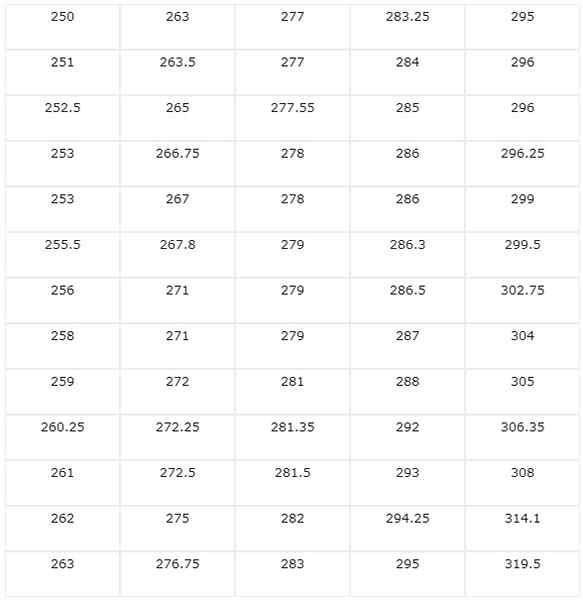
The following results are obtained: 251 252.5 314.1 263 305 319.5 265 267.8 304 306.35 262 250 308 302.75 256 258 267 277.55 281.35 255.5 253 259 263 266.75 278 295 296 299.5 263.5 261 260.25 277 272.5 286 295 279 272.25 286.3 279 296.25 271 272 279 275 277 279 276,75 281 287 286,5 294,25 285 288 296 283,25 281,5 293 284 282 292 299 283

1.- Tilataan heidät nousevassa järjestyksessä

2.- Taajuustaulukon rakentamiseksi meidän on määritettävä: variaation amplitudi, luokkien lukumäärä ja luokkaväli

Luokkien lukumäärä valitaan ajatellen, että ne ovat vähän luokkia ja lähes 70 variaation amplitudin jakajissa.

Voi palvella sinua: fraktiot vastaavat 2/3

7 luokkaa on mukava määrä hallitaan luokkia ja luokkavälejä pysyy 10: ssä, mikä on ihanteellinen määrä ryhmiteltyjen tietojen kanssa.

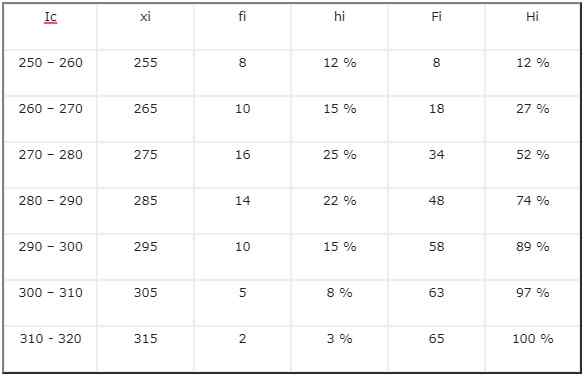
3.- Rakennamme kuuden saraketaulun

- Luokkaväli (IC), joka edustaa luokkaa (luokkaväli), tässä tapauksessa luokkaan sisältyvien palkkojen ala- ja ylärajat.

- Luokkakeskus (XI), joka edustaa luokan keskimääräistä luokkaarvoa.

- Absoluuttinen taajuus (FI), joka edustaa absoluuttista taajuutta, tässä tapauksessa luokkaan kuuluvien palkkojen lukumäärä.

- Suhteellinen taajuus (HI) on absoluuttisen taajuuden (FI) ja datan kokonaismäärän (n) välinen osuus, joka on ilmaistu prosentteina.

- Kertynyt absoluuttinen taajuus (FI) osoittaa, kuinka monta dataluettelon elementtiä on pienempi tai yhtä suuri kuin tietyn luokan yläraja. Se on absoluuttisten taajuuksien summa ensimmäisestä luokasta valittuun luokkaan.

- Kertynyt suhteellinen taajuus (HI), on kertyneen absoluuttisen taajuuden (FI) ja datan kokonaismäärän (n) välinen osoitus, joka on ilmaistu prosentteina.

Taulukko pysyy:

On huomattava, että suhteellinen taajuus voi olla absoluuttinen tai kertynyt, ja eli suhteellisen taajuuden käsite asettaa meidät vertailun kokonaismäärään. Mikä tahansa määrä voidaan laskea tämän tyyppisillä indekseillä.

Esimerkiksi, kun puhumme tietyssä testissä tai kokeessa hyväksyttyjen opiskelijoiden prosenttiosuudesta, tämä prosenttiosuus on testin tai tentin hyväksyneiden opiskelijoiden osuus; toisin sanoen se on opiskelijoiden kokonaismäärään liittyvä määrä.

Voi palvella sinua: Rhomboid: Ominaisuudet, kuinka kehä ja alue vie pois

Bibliografia kuuli

1. Canavos, G. 1988. Todennäköisyys ja tilastot. Sovellukset ja menetelmät. McGraw-Hill/Amerikanvälinen Meksikosta. -Lla. C: n. V. Meksiko. 667 p.
2. Freund, r. ja Wilson, W. 2003. Tilastolliset menetelmät. Toinen ED. Akateeminen lehdistö. Jäljennös Elsevier -tieteestä. San Diego. Käyttötarkoitukset. 694 p.
3. Sokal, r. ja Rohlf, f. 1979. Biometria. Tilastolliset periaatteet ja menetelmät biologisessa tutkimuksessa. H. Blume -versiot. Meksiko. 832 p.
4. Spiegel, M. 1991. Tilastot. Toinen ED. McGraw-Hill/Amerikanvälinen Espanjasta. -Lla. Madridi. 572 p.
5. Walpole, r., Myers, r., Myers, S. Ja te, ka. 2007. Todennäköisyys ja tilastot insinööreille ja tutkijoille. Kahdeksas ed. Pearson Education International Prentice Hall. New Jersey. Käyttötarkoitukset. 823 p.