Vapaat vektorien ominaisuudet, esimerkit, harjoitukset

Se ilmaiset vektorit He ovat niitä, jotka on täysin määritelty niiden suuruudesta, suunnastaan ​​ja merkityksestään, ilman että on tarpeen osoittaa sovelluspiste tai tietty alkuperää.

Koska äärettömät vektorit voidaan piirtää tällä tavalla, vapaa vektori ei ole ainutlaatuinen kokonaisuus, vaan joukko rinnakkaisia ​​ja identtisiä vektoreita, jotka ovat riippumattomia paikasta, jossa ne sijaitsevat.

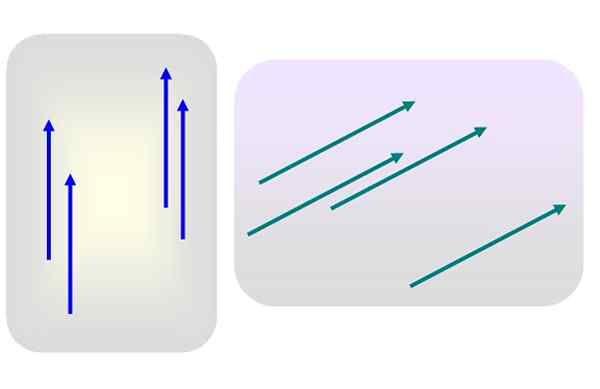
Kuvio 1. Erilaisia ​​ilmaisia ​​vektoreita. Lähde: Itse tehty.

Sanotaan.

Mitään näistä vektoreista ei sovelleta erityisesti jossain pisteessä. Silloin mitä tahansa sinistä tai vihreää vektoria edustavat heidän ryhmäänsä, koska sen ominaisuuksia - moduulia, suuntaa ja järkeä - ei muuteta ollenkaan, kun ne siirretään toiseen tasoon tasoon.

Ilmainen vektori merkitään yleensä painetussa tekstissä, jossa on pieni ja rohkea kirjain, esimerkiksi v. Tai pienillä kirjaimilla ja nuolella päällä, jos se on käsikirjoitusteksti.

[TOC]

 Esimerkit

Vapaiden vektorien etuna on, että niitä voidaan siirtää lentokoneella tai avaruudella ja ylläpitää niiden ominaisuuksia, koska jokainen sarjan edustaja on yhtä pätevä.

Siksi fysiikassa ja mekaniikassa käytetään usein. Esimerkiksi liikuttavan kiinteän aineen lineaarisen nopeuden osoittamiseksi ei ole tarpeen valita objektin tiettyä pistettä. Sitten nopeusvektori käyttäytyy kuin vapaa vektori.

Toinen esimerkki vapaasta vektorista on voimat. Eräs pari Se koostuu kahdesta yhtä suuresta ja suunnasta, mutta vastakkaisista aisteista, joita käytetään kiinteän aseman eri kohdissa. Parin vaikutuksena ei ole siirtää kohdetta, vaan aiheuttaa kiertoa hetki tuotettu.

Kuvio 2 esittää ohjauspyörään levitetyn voiman pari. Voimien kautta F₁ ja F₂, Vääntömomentti, joka kääntää ohjauspyörän keskuksen ympärille, luodaan ja aikataulussa.

Se voi palvella sinua: boorinitride (BN): rakenne, ominaisuudet, hankkiminen, käyttö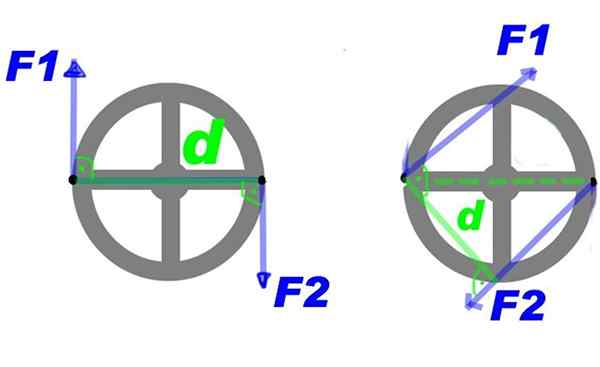 Kuva 2. Muutama ohjauspyörään kohdistetut voimat tarjoavat pisteytyksen. Lähde: Bensko [julkinen alue].

Voit tehdä joitain muutoksia parissa ja jatkaa saman kiertävän vaikutuksen saamista, esimerkiksi lisätä voimaa, mutta vähentää niiden välistä etäisyyttä. Tai ylläpitää voimaa ja etäisyyttä, mutta levitä pari vielä pari pistettä ohjauspyörällä, toisin sanoen kääntämällä vääntömomentti keskustan ympärille.

Joukkojen parin tai yksinkertaisesti pari, Se on vektori, jonka moduuli on FD ja on kohtisuorassa pyörätasoon kohtisuoraan. Yleissopimuksen esittämässä esimerkissä aika kääntyy kielteisesti.

Ominaisuudet ja ominaisuudet

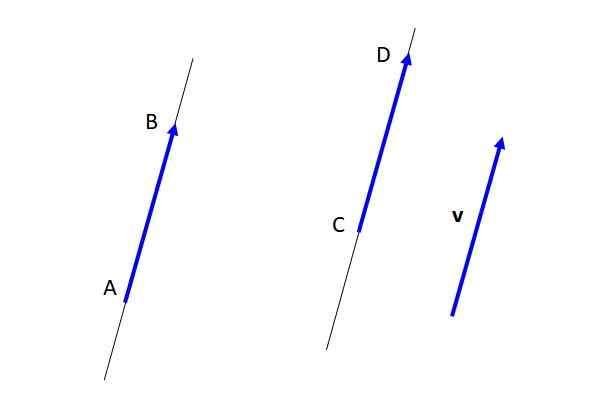
Toisin kuin vapaa vektori v, vektorit Ab ja CD Ne ovat kiinteitä (katso kuva 3), koska he ovat määritelleet lähtökohdan ja saapumispisteen. Mutta olla varusteita keskenään ja vuorostaan ​​vektorin kanssa v, He edustavat vapaata vektoria v.

Kuva 3. Vapaat vektorit, laitteet ja kiinteät vektorit. Lähde: Itse tehty.

Vapaiden vektorien pääominaisuudet ovat seuraavat:

-Mikä tahansa vektori Ab (Katso kuva 2) Se on ilmaisen vektorin edustaja, kuten todetaan v.

-Moduuli, suunta ja merkitys ovat samat missä tahansa vapaassa vektorissa. Kuviossa 2 vektorit Ab ja CD Ne edustavat ilmaista vektoria v Ja ne ovat laitteita.

-Avaruuden pisteen P on aina mahdollista löytää vapaa vektorien edustaja v jonka alkuperä on P: ssä ja mainittu edustaja on ainutlaatuinen. Tämä on ilmaisten vektorien tärkein ominaisuus ja se, joka tekee heistä niin monipuolisia.

Voi palvella sinua: Eurooppa (satelliitti): Ominaisuudet, koostumus, kiertorata, liike

-Voyed ilmainen vektori on merkitty nimellä 0 - Ja kaikki vektorit, joilla ei ole suuruutta, suunta ja merkitys.

-Jos vektori Ab edustaa vapaata vektoria v, Sitten vektori Ba edustaa vapaata vektoria -v.

-Merkintää käytetään V³ kaikkien avaruusvapaiden vektorien ja V² Määrittää kaikki lentokoneen vapaat vektorit.

Ratkaisut

Ilmaisilla vektoreilla voit suorittaa seuraavat toiminnot:

-Lisäys

-Vähennyslasku

-Kiipeilyn kertominen vektorilla

-Skalaarituote kahden vektorin välillä.

-Ristituote kahden vektorin välillä

-Vektorien lineaarinen yhdistelmä

Ja enemmän.

-Harjoitus 1

Opiskelija aikoo uida rannan pisteestä joesta toiseen, joka on juuri edessä. Saavuttaakseen mitään suoraan nopeudella 6 km / h, kohtisuorassa, mutta virran nopeus on 4 km / h, joka ohjaa sen.

Laske uimarista johtuva nopeus ja kuinka paljon virran ohjaaminen.

Ratkaisu

Uimurin pidennysnopeus on sen nopeuden vektorisumma (joen suhteen, vedetty pystysuoraan ylöspäin) ja joen nopeus (vedetty vasemmalta oikealle), joka suoritetaan alla olevan kuvan mukaisesti:

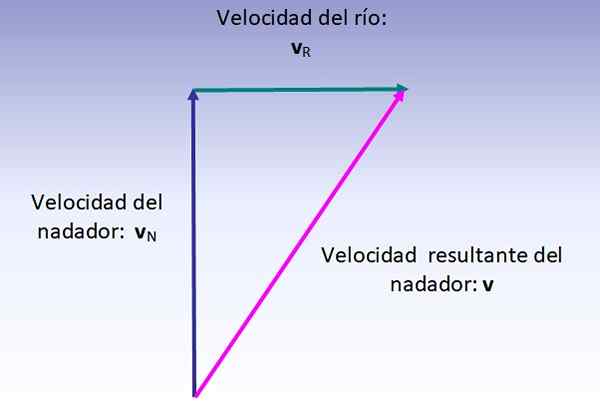
Tuloksena olevan nopeuden suuruus vastaa esitetyn oikean kolmion hypotenusia, siksi:

V = (6² + 4²-A ^½ km/h = 7.2 km/h

Osoite voidaan laskea kulmalla suhteessa kohtisuoraan rantaan:

α = arctg (4/6) = 33.7. tai 56.Kolmas rannalla.

Harjoitus 2

Löydä kuvassa esitettyjen voimien parin aika:

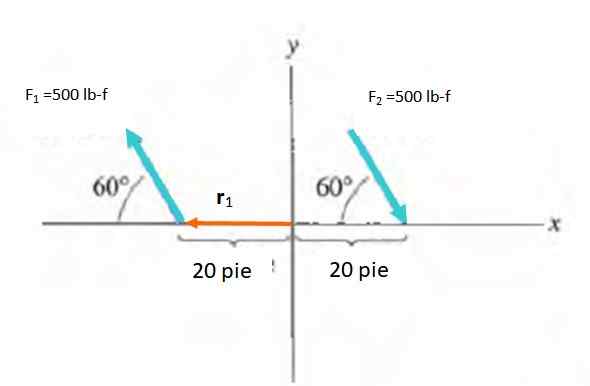
Ratkaisu

Hetki lasketaan:

Voi palvella sinua: joustavat iskut: ulottuvuudessa ja esimerkeissä

M = r - x F

Hetken yksiköt ovat LB-F.jalka. Koska vääntömomentti on näytön tasossa, hetki on suunnattu kohtisuoraan siihen, joko ulospäin tai sisäänpäin.

Koska esimerkin vääntömomentti pyrkii kääntämään objektia, johon sitä käytetään (jota ei esitetä kuvassa) aikataulussa, tätä hetkeä otetaan huomioon osoittamalla näytön sisälle ja negatiivisella merkinnällä.

Hetken suuruus on m = f.d -d.synti A, oleminen voiman ja vektorin välillä r -. Sinun on valittava kohta, jolle hetki voidaan laskea, mikä on vapaa vektori. Siksi valitaan vertailujärjestelmän alkuperä, r - siirtyy O: sta kunkin voiman levityspisteeseen.

M₁ = M₂ = -Fdsen60º = -500 . kaksikymmentä .SEN 60º LB-F . jalka = -8660.3 lb-f . jalka

Nettomomentti on m: n summa₁ ja m₂: -17329.5 lb-f . jalka.

Viitteet

1. Beardon, t. 2011. Johdatus vektoriin. Toipunut: Nrich.Matematiikka.org.
2. Bedford, 2000. -Lla. Tekniikan mekaniikka: staattinen. Addison Wesley. 38-52.
3. Figueroa, D. Sarja: Tieteen ja tekniikan fysiikka. Osa 1. Kinematiikka.31-68.
4. Fyysinen. Moduuli 8: Vektorit. Toipunut: FRTL.Utn.Edu.AR
5. Hibbeler, R. 2006. Insinöörien mekaniikka. Staattinen. 6. painos. Mannertoimitusyhtiö. 15-53.
6. Lisäyslaskinvektori. Toipunut: 1728.org
7. Vektorit. Palautettu: se on.Wikibooks.org