Tuloksena oleva vektorilaskelma, esimerkit, harjoitukset

Hän tuloksena oleva vektori Se on se, joka on saatu operaatiolla vektoreilla, joiden tulos on myös vektori. Normaalisti tämä operaatio on kahden tai useamman vektorin summa, jonka kautta saadaan vektori, jonka vaikutus on vastaava.

Tällä tavalla saadaan vektorit, kuten nopeus, kiihtyvyys tai voima. Esimerkiksi kun useita voimia toimivat ruumiissa F₁, F₂, F₃,.. . Kaikkien näiden voimien vektorisumma vastaa nettovoimaa (tuloksena), joka matemaattisesti ilmaisee:

F₁ + F₂ + F₃ +… = F_{R -}  jompikumpi F_N

Kuvio 1. Luntapaino jakautuu kattoon ja sen toiminta voidaan korvata yhdellä tuloksena olevalla voimalla, jota kohdistetaan asianmukaiseen paikkaan. Lähde: Pixabay.

Tuloksena oleva vektori, olipa kyse sitten voimista tai muusta vektorin suuruudesta, soveltaa vektorien summan sääntöjä. Koska vektoreilla on suunta ja järki numeerisen arvon lisäksi, moduulien lisäämiseen saadaan saatu vektori lisäämään.

Tämä on totta vain siinä tapauksessa, että mukana olevat vektorit ovat samaan suuntaan (katso esimerkit). Muutoin on tarpeen käyttää vektorisummenetelmiä, jotka tapauksesta riippuen voivat olla geometrisiä tai analyyttisiä.

[TOC]

Esimerkit

Geometriset menetelmät tuloksena olevan vektorin löytämiseksi ovat Polygon -menetelmä ja rinnakkaisohjelma menetelmä.

Analyyttisten menetelmien suhteen on komponenttimenetelmä, jonka kautta löytyy mistä tahansa vektorijärjestelmästä johtuva vektori, kunhan se on sen Cartesian -komponentit.

Geometriset menetelmät kahden vektorin lisäämiseksi

Oletetaan, että vektorit tai ja v (Merkitsemme heitä lihavoituna erottamaan heidät skalaarista). Kuvassa 2) meillä on ne sijaitsevat lentokoneessa. Kuviossa 2 b) se on siirtynyt vektorille V siten, että sen alkuperä on samaan aikaan tai. Tuloksena oleva vektori siirtyy ensimmäisen alkuperästä (tai) viimeisen kärkeen (v)

Se voi palvella sinua: puristus: Kiinteät aineet, nesteet, kaasut, esimerkit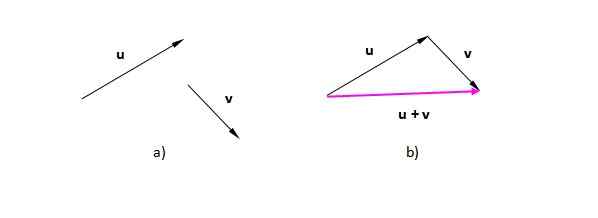 Kuva 2. Tuloksena oleva vektori vektorien graafisesta summasta. Lähde: Itse tehty.

Kuva, joka johtaa tässä tapauksessa, on kolmio (kolmio on 3 -puolinen monikulmio). Jos meillä on kaksi vektoria samaan suuntaan, menettely on sama: Aseta yksi vektoreista toisensa jälkeen ja piirtää yhden, joka menee ensimmäisen alkuperästä tai hänestä viimeisen kärkeen tai päähän.

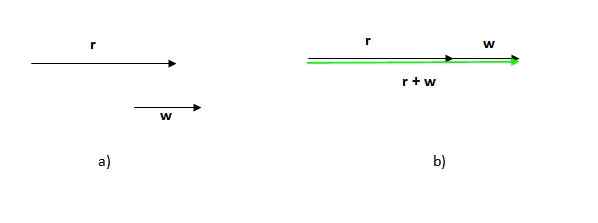
Huomaa, että tämän menettelyn tekemisjärjestyksellä ei ole merkitystä, koska vektorien summa on kommutatiivinen.

Huomaa myös, että tässä tapauksessa moduuli (Tuloksena olevan vektorin pituus tai koko) on lisävektorien moduulien summa, toisin kuin edellisessä tapauksessa, jossa tuloksena oleva vektorimoduuli on pienempi kuin osallistujien moduulien summa.

Rinnakkaisohjelma

Tämä menetelmä on erittäin sopiva, kun joudut lisäämään kaksi vektoria, joiden lähtökohdat ovat yhtä mieltä, X-Y-koordinaattijärjestelmän alkuperän kanssa. Oletetaan, että näin on vektorimme tai ja v (Kuva 3):

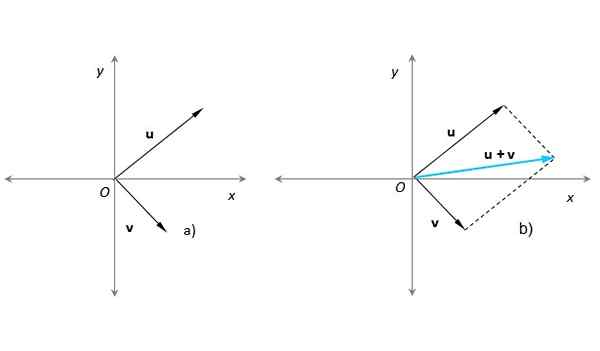Kuva 3. Kahden vektorin summa rinnakkaisogrammimenetelmän avulla tuloksena olevan vektorin kanssa turkoosi sinisellä. Lähde: Itse tehty.

Kuviossa 3b) rinnakkaisgrammi on rakennettu rinnakkain katkoviivojen avulla tai jo v. Tuloksena oleva vektori on lähtökohta O: sta ja sen päätä siinä vaiheessa, jossa katkoviivat leikkaavat. Tämä menettely on täysin vastaava edellisessä osassa kuvattu.

Harjoitukset

-Harjoitus 1

Seuraavat vektorit, etsi tuloksena oleva vektori monikulmaisen menetelmän avulla.

Se voi palvella sinua: kevyt heijastus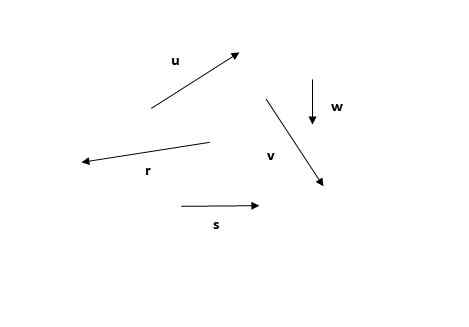 Kuva 4. Vektorit löytääkseen sen tuloksena monikulmion menetelmän avulla. Harjoitus 1. Lähde: Itse tehty.

Ratkaisu

Polygonaalinen menetelmä on ensimmäinen havaituista menetelmistä. Muista, että vektorien summa on kommutatiivinen (lisäysten järjestys ei muuta summaa), joten voit aloittaa esimerkiksi jollain vektoreilla tai (Kuva 5a) tai r - (Kuva 5b):

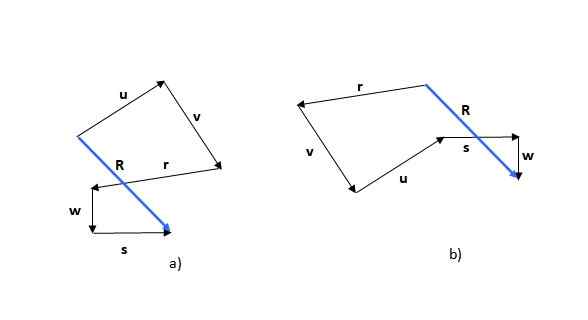Kuva 5. Vektorien summa monikulmion menetelmän avulla. Lähde: Itse tehty.

Saatu kuva on monikulmio ja tuloksena oleva vektori (sinisellä) kutsutaan R -. Jos aloitat toisella vektorilla, muodostettu luku voi olla erilainen, kuten esimerkissä voidaan nähdä, mutta tuloksena oleva vektori on sama.

Harjoitus 2

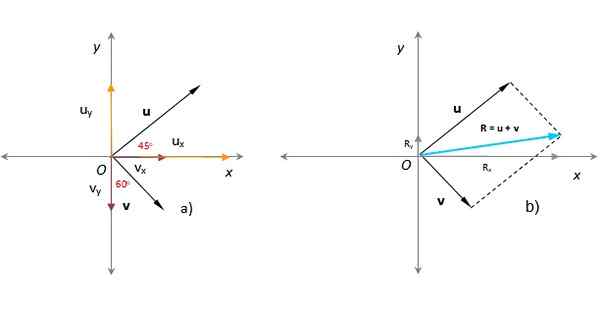
Seuraavassa kuvassa tiedetään, että vektorien moduulit tai ja v vastaavasti ovat U = 3 mielivaltaisia ​​yksiköitä ja v = 1.8 mielivaltaista yksikköä. Kulma että tai muodostuu positiivisella X -akselilla on 45 º, kun taas v Muodosta 60 º Y -akselin kanssa, kuten kuvassa nähdään. Etsi tuloksena oleva vektori, suuruus ja suunta.

Ratkaisu

Edellisessä osassa tuloksena saatu vektori havaittiin rinnakkaisohjelman menetelmän soveltamisen (kuvassa turkoosi).

Yksinkertainen tapa löytää tuloksena oleva vektori analyyttisesti on ilmaista vektorit, jotka lisäävät heidän karteesikomponentteja, mikä on helppo tehtävä, kun moduuli ja kulma tunnetaan, kuten tämän esimerkin vektorit:

tai_x = u . cos 45º = 3 x cos 45 º = 2.12; tai_ja = u . SIN 45 º = 3x Sen 45º = 2.12

v_x = v . SEN 60º = 1.8 x sen 60 º = 1.56; v_ja = -V . cos 60 º = -1.8 x cos 60º = - 0.9

Voi palvella sinua: Pendulaarinen liike

Vektorit tai ja v Ne ovat lentokoneeseen kuuluvia vektoreita, joilla on molemmat kaksi komponenttia. U -vektori on ensimmäisessä kvadrantissa ja sen komponentit ovat positiivisia, kun taas vektori V on neljännessä kvadrantissa; Sen X -komponentti on positiivinen, mutta sen projektio pystysuuntaisella akselilla putoaa akseliin ja negatiiviseen.

Tuloksena olevan vektorin Cartesian -komponenttien laskeminen

Tuloksena oleva vektori lisää algebrallisesti vastaavia komponentteja X ja Y, jotta saadaan sen Cartesian -komponentit:

R -_x = 2.12 + 1.56 = 3.68

R -_ja = 2.12 + (-0.9) = 1.22

Kun Cartesian -komponentit on määritelty ja vektori tunnetaan kokonaan. Tuloksena oleva vektori voidaan ilmaista merkinnällä neliöhakeissa (haarut)

R = mielivaltaiset yksiköt

Kiinnitysmerkintä käytetään erottamaan vektori tasosta (tai avaruudessa). Toinen tapa ilmaista tuloksena oleva vektori analyyttisellä tavalla on yksikkövektoreiden käytön avulla Yllyttää ja J koneessa (Yllyttää, J - ja k -k - avaruudessa):

R - = 3.68 Yllyttää + 1.22 J - mielivaltaiset yksiköt

Koska tuloksena olevan vektorin molemmat komponentit ovat positiivisia, vektori R - Se kuuluu ensimmäiseen kvadranttiin, joka oli jo nähty graafisesti.

Tuloksena olevan vektorin suuruus ja suunta

Cartesian -komponenttien tunnetuksi R -suuruus lasketaan Pythagoras -lauseen läpi, koska tuloksena oleva vektori R -, sen komponenttien r_x ja r_ja Ne muodostavat oikean kolmion:

Suuruus tai moduuli: r = (3.68² + 1.22²-A^½ = 3.88

Osoite q Positiivisen X -akselin ottaminen referenssinä: Q = Arcan (R_ja / R_x) = arctg (1.22/3.68) = 18.Kolmas

Viitteet

1. Vektorien ja sääntöjen lisääminen. Toipunut: Newt.Fyysinen.Vatsan.Edu.Au
2. Figueroa, D. Sarja: Tieteen ja tekniikan fysiikka. Osa 1. Kinematiikka.31-68.
3. Fyysinen. Moduuli 8: Vektorit. Toipunut: FRTL.Utn.Edu.AR
4. Hibbeler, R. 2006. Insinöörien mekaniikka. Staattinen. 6. painos. Mannertoimitusyhtiö. 15-53.
5. Lisäyslaskinvektori. Toipunut: www.1728.org