Ominaisuusyksikkövektorit, miten se pääsee, esimerkkejä

Se yksikkövektorit ovat niitä, joiden moduuli, suuruus tai koko on yhtä suuri kuin numeerinen arvo. Yksikkövektorit ovat hyödyllisiä osoittamaan muiden ei -yksikkövektorien suunta.

Muista, että vektorit ovat matemaattisia kokonaisuuksia, jotka edustavat matemaattisesti suunnasta riippuvia fyysisiä suuruuksia, kuten vahvuus, nopeus, kiihtyvyys ja muut.

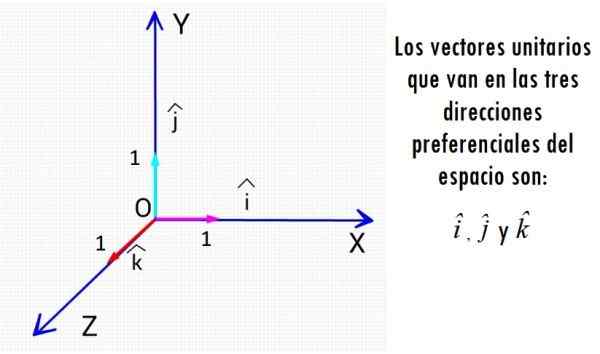
Tunnetuimmat yksikkövektorit ovat kolme vektoria, jotka kulkevat Cartesian akselien suunnissa. Lähde: f. Zapata.

Liittyvästä fyysisestä suuruudesta riippumatta yksikkövektorit ovat kokonaisuuksia, joilla ei ole mittayksiköitä ja niiden koko on aina 1, puhdas luku.

Esimerkiksi hiukkasen nopeus, joka liikkuu 3 m/s ja menee Cartesian X -akselin positiiviseen suuntaan, merkitään: v = (3 m/s) Yllyttää, missä rohkeaa kirjettä käytetään vektorimäärien merkitsemiseen. Tässä esimerkissä moduuli v Se on 3 m/s ja yksikkövektorimoduuli Yllyttää on 1 (ilman yksiköitä).

[TOC]

Moduuli, suunta ja merkitys

Kun otetaan huomioon. Vektorimäärän esittämishetkellä on tarpeen ilmoittaa nämä näkökohdat selvästi.

Nyt yksikkövektorilla voi olla mikä tahansa suunta ja edullinen merkitys, mutta suuruuden on aina oltava yhtä suuri kuin 1.

Yksikkövektoreita käytetään osoittamaan yksityinen osoite avaruudessa tai lentokoneessa. Jos esimerkiksi meidän on työskenneltävä kaikkien vaakasuuntaista akselin varrella toimivien voimien kanssa, koska yksikkövektori siihen suuntaan auttaa meitä erottamaan nämä voimat muista suuntaan suunnattuista.

Ja erottaakseen heidät muista kuin yksikkövektoreista, lihavoitu käytetään yleensä painetussa ja asettamalla ympyrän aksentti esimerkiksi:

Se voi palvella sinua: Kiinteä valtion teoria: Historia, selitys, uutiset

Käsinkirjoitettuihin sanoituksiin riittää asettamaan ympyrän ymmärtäminen ymmärtämään, että se on yksikkövektori.

Yksikkövektorin ominaisuudet

Matemaattisesti yksikkövektori:

Se on elementti, joka kuuluu ulottuvuuden n vektoritilaan ℛ siten, että |vJa = 1, missä palkit tarkoittavat "moduulia".

Joten voimme selvittää sen:

-Yhtenäinen vektorimoduuli on aina 1, sillä ei ole väliä onko se vahvuus, nopeus vai muu vektori.

-Yksikkövektoreilla on tietty suunta, samoin kuin suunta, kuten yksikkövektori pystysuunnassa, jotka voivat olla järkeviä ylös tai alas.

-Yksikkövektoreilla on alkuperäpiste. Kartesialainen koordinaattijärjestelmä edustaa, että piste on samanaikainen järjestelmän alkuperän kanssa: (0,0) Jos se on taso tai (0,0,0), jos vektori on kolmen dimensionaalisessa tilassa.

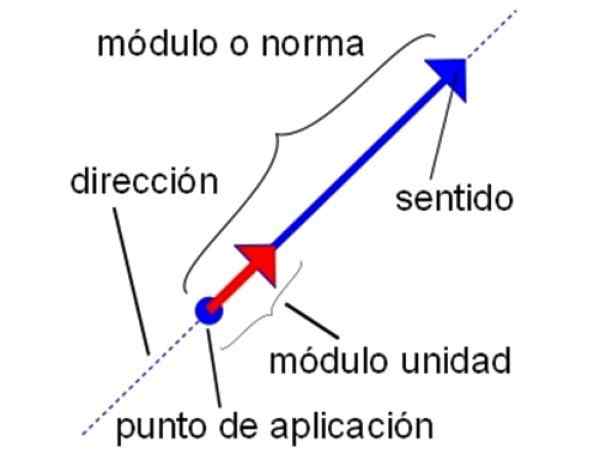Yksikkövektorin ominaisuudet. Lähde: Wikimedia Commons.

-Myös yksikkövektorien kanssa kaikki tavallisilla vektoreilla tehdyt summa-, vähennys- ja vektorikertomustoiminnot voidaan suorittaa. Siksi on pätevä moninkertaistaa yksikkövektori skalaarilla, samoin kuin pistemäärän ja ristikkäisen tuotteen suorittaminen.

-Yksikkövektori tiettyyn suuntaan voidaan ilmaista myös muita vektoreita, jotka ovat myös suuntautuneet siihen suuntaan.

Yksikkövektorit avaruudessa

Kaikkien vektorien ilmaisemiseksi avaruudessa tai tasossa voit käyttää joukkoa yhtenäisiä vektoreita kohtisuorassa toisiinsa nähden, jotka muodostavat Ortonormal -pohjan. Jokaisella avaruussuunnitelmassa on oma yksikkövektori.

Palataan takaisin vaaka -akselia pitkin suunnattujen voimien esimerkkiin. Tämä on X -akseli, jolla on kaksi mahdollisuutta: suunta oikealle ja suunta vasemmalle. Oletetaan

Voi palvella sinua: Thomson Atomic -malli: Ominaisuudet, postulaatit, subatomiset hiukkaset

Jokainen niistä on voimassa. Oletetaan nyt, että voima F₁ suuruusluokka 5 N tätä akselia pitkin ja suunnattu oikealle, tällainen voima voitiin ilmaista seuraavasti:

Jos voima ohjataan X -akselia pitkin, mutta vastakkaiseen suuntaan, toisin sanoen vasemmalle, tämän eron määrittämiseen voitaisiin käyttää negatiivista merkkiä.

Esimerkiksi 8 N: n suuruusvoima, joka sijaitsee X -akselilla ja suunnattu vasemmalle, olisi tällainen:

Tai niin:

Ja vektoreille, joita ei ole suunnattu Cartesian akselia pitkin, on myös tapa edustaa niitä ortogonaalisten yksikkövektoreiden suhteen Cartesian komponenttien kautta.

Yksikkövektorin poistaminen/laskeminen?

Yksikkövektorin laskeminen mielivaltaisen vektorin suuntaan v, Seuraavaa kaavaa käytetään:

Missä:

Se on vektorin moduuli tai suuruus v, jonka neliö on laskettu näin:

JavJa² = (v_x-A² +  (V_ja-A²+  (v_{z -z}-A²

Mielivaltainen vektori yksikkövektorin suhteen

Vaihtoehtoisesti vektori v Se voidaan ilmaista seuraavasti:

Toisin sanoen sen moduulin tuote vastaavalla yksikkövektorilla. Juuri tämä tehtiin aikaisemmin, kun puhutaan 5 N: n voimakkuuden voimasta, joka on suunnattu positiivista X -akselia pitkin.

Graafinen esitys

Graafisesti mitä sanotaan tässä kuvassa, missä vektori v Se on sinisellä ja vastaava yksikkövektori sen suuntaan on punaisella.

Tässä esimerkissä vektori v Sen suuruus on suurempi kuin yksikkövektorissa, mutta selitys on jopa pätevä, jos näin ei tapahdu. Toisin sanoen meillä voi olla vektoreita, jotka ovat esimerkiksi 0.25 kertaa yksikkövektori.

Voi palvella sinua: Paino (fyysinen): Laskenta, yksiköt, esimerkit, harjoitukset

Esimerkkejä yksikkövektoreista

Kohtisuorayksikkövektorit I, J ja K

Kuten olemme aiemmin nähneet, kohtisuora yksikkövektorit Yllyttää, J - ja k -k - Ne ovat erittäin hyödyllisiä edustaa mitä tahansa muuta vektoria koneessa tai tilassa ja suorittamaan vektorioperaatioita. Mainitun vektorin kannalta mielivaltainen vektori V on esitetty seuraavasti:

v = v_x Yllyttää + v_ja J - + v_{z -z} k -k -

Missä v_x, v_ja ja v_{z -z} ovat vektorin suorakulmaisia ​​komponentteja v, jotka ovat kiipeilyä -ei käytetä niiden edustamiseen painettuna tekstissä-.

Coulombin laki

Yhtenäiset vektorit esiintyvät usein fysiikassa. Siellä meillä on esimerkiksi Coulombin laki, joka kuvaa kvantitatiivisesti kahden erityisen sähköisen varauksen vuorovaikutusta.

Se osoittaa, että voima F Näiden kuormien välinen vetovoima tai torjunta on verrannollinen niiden tuotteeseen, käänteisesti verrannollinen ne erottelevan etäisyyden neliöön ja ohjataan kuormitukseen liittyvän yksikkövektorin suuntaan, joka liittyy yksikkövektorin suuntaan.

Tätä vektoria edustaa yleensä:

Ja Coulombin laki on tällainen vektorimuodossa:

Missä k -k - Se on sähköstaattinen vakio, Q -₁ ja Q -₂ Ne ovat kuormia ja r - Etäisyys erottaa ne.

Liikuntaa

Etsi yksikkövektori vektorin suuntaan v = 5Yllyttää + 4J - -8k -k -, Annetaan mielivaltaisissa yksiköissä.

Ratkaisu

Yllä olevasta yhtenäisen vektorin määritelmää sovelletaan yllä:

Mutta ensin sinun on laskettava vektorimoduuli, joka sillä on kolme komponenttia, määritetään:

JavJa² = (v_x-A² +  (V_ja-A² +  (V_{z -z}-A²

Pysyminen:

JavJa² = (5)² +  (4)² +  (-8)²= 25 + 16 + 64 = 105

Siksi moduuli v On:

Jav| = √105

Etsijä yhtenäinen vektori on yksinkertaisesti:

Se johtaa lopulta:

v = 0.488 Yllyttää + 0 -.390 J - - 0 -.781 k -k -

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill.
2. Bedford, 2000. -Lla. Tekniikan mekaniikka: staattinen. Addison Wesley.
3. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Osa 1. Kinematiikka. Toimittanut Douglas Figueroa (USB).
4. Giambattista, a. 2010. Fysiikka. Toinen. Ed. McGraw Hill.
5. Resnick, r. (1999). Fyysinen. Osa. 1. 3. ed. espanjaksi. Mannertoimitusyhtiö S.-Lla. C: n.V.