Kulmanopeuden määritelmä, kaava, laskenta ja harjoitukset

Se kulmanopeus Se on pyörimisnopeuden mitta ja se on määritelty kulmana, joka kiertää kohteen asentovektoria, joka pyörii, aikayksikköä kohti. Se on voimakkuus, joka kuvaa erittäin hyvin monien esineiden liikettä, jotka jatkuvasti kääntyvät kaikkialle: CD -levyjä, autopyöriä, koneet, maa ja monet muut.

"London Eye" -järjestelmä näkyy seuraavassa luvussa. Se edustaa pisteen P edustaman matkustajan liikettä, joka seuraa pyöreää suuntausta, nimeltään C:

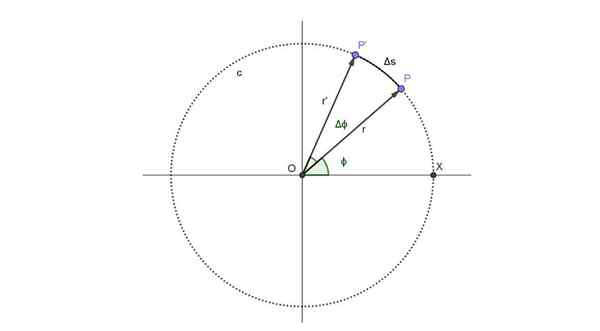Kaavamainen esitys pyöreästä etenemissuunnasta, joka seuraa "London Eye" -matkustajaa. Lähde: Itse tehty.

Matkustaja miehittää aseman P hetkessä p ja sitä hetkeä vastaava kulma -asema on ϕ.

Hetkestä lähtien, kun aika on kulunut Δt. Tuona ajanjaksona täsmällisen matkustajan uusi sijainti on P 'ja kulma -asema on lisännyt kulmaa δϕ.

[TOC]

Kuinka kulmanopeus lasketaan ?

Kiertomatkat, kreikkalaisia ​​kirjaimia käytetään laajasti, niiden erottamiseksi lineaarisista suuruuksista. Joten aluksi määritetään keskimääräinen kulmanopeus ω_m Kun kulma kulki tietyllä ajanjaksolla.

Sitten osamäärä Δϕ/ΔT edustaa keskimääräistä kulmanopeutta ω_m Momenttien joukossa T ja T+ΔT.

Jos haluat laskea kulmanopeus Juuri silloin t, sitten osamäärä Δϕ/ΔT on laskettava, kun ΔT ➡0:

 Kulanopeuden mitta on rad/s.

Lineaarisen ja kulmanopeuden välinen suhde

Lineaarinen nopeus v, Se on osamäärä kuluneen matkan ja sen kuluttamiseen käytetyn ajanjakson välillä.

Yllä olevassa kuvassa kaarireitti on ΔS. Mutta tuo kaari on verrannollinen kulmaan kulkevaan kulmaan ja säteeseen, joka täyttää seuraavan suhteen, mikä on pätevää niin kauan kuin Δϕ mitataan radiaaneissa:

Voi palvella sinua: Parallegrammimenetelmä: Esimerkkejä, ratkaisut harjoitukset

ΔS = r ・ Δϕ

Jos jaamme edellisen lausekkeen ajanjakson ΔT välillä ja otamme rajan, kun Δt ➡0, saamme:

v = r ・ ω

Tasainen kiertoliike

Kuva on kuuluisa ”London Eye”, 135 metriä korkea pyörivä pyörä, joka pyörii hitaasti, jotta ihmiset voivat nousta hytteihin tukikohdassaan ja nauttia Lontoon maisemasta. Lähde: Pixabay.

Kiertoliike on tasainen, jos kulma kulma on samana ajanjaksona, jos sitä havaitaan milloin tahansa, samana ajanjaksona.

Jos kierto on tasaista, niin kulmanopeus milloin tahansa tapahtuu keskimääräisen kulmanopeuden kanssa.

Yhtenäisessä kiertoliikkeessä aika, jolloin täydellistä käännöstä kutsutaan ajanjaksoksi, ja se merkitsee T: llä.

Lisäksi kun kulma käännetään ympäri, se on 2π (vastaa 360º). Siksi yhtenäisessä kiertokunnassa kulmanopeus ω liittyy ajanjaksoon t seuraavan kaavan avulla:

Taajuus on määritelty F yhtenäisestä kiertosta, kuten osamäärä käännösten lukumäärän ja niiden matkustamisessa käytetyn ajan välillä. Kun paluu, se kulkee aikaan T (ajanjaksolla) on seuraava suhde:

F = 1/t

Toisin sanoen yhtenäisessä kiertossa kulmanopeus liittyy taajuuteen:

Ω = 2π ・ f

Ratkaistu kulmanopeusharjoitukset

Harjoitus 1

Suuren pyörivän pyörän hyttit, jotka tunnetaan nimellä "Lontoon silmä"Ne liikkuvat hitaasti. Mökkien nopeus on 26 cm/s ja pyörän halkaisija on 135 m.

Tämän tiedon kanssa lasketaan:

Voi palvella sinua: aurinko

i) pyörän kulmanopeus

ii) kiertotaajuus

iii) Aika, joka vie matkustamon kääntymiseen.

Vastaukset:

Yo) Nopeus v m/s on: V = 26 cm/s = 0,26 m/s.

Radio on halkaisijan puolet: r = (135 m) / 2 = 67,5 m

V = r ・ ω => ω = V/r = (0,26 m/s)/(67,5 m) = 0,00385 rad/s

Ii) Ω = 2π ・ f => f = ω / 2π = (0,00385 rad / s) / (2π rad) = 6,13 x 10^-4 käännökset/s

F = 6,13 x 10^-4 käänny/s = 0,0368 käänny/min = 2,21 käännöstä/tunti.

Iii) T = 1 / f = 1/21 käännös / tunti = 0,45311 aika = 27 min 11 sekunnin

Harjoitus 2

Leluauto liikkuu 2 m: n säteen pyöreällä radalla. 0 s sen kulma -asema on 0 rad, mutta ajan kuluttua t sen kulma -asema on annettu:

φ (t) = 2 ・ t 

Päättää:

i) kulmanopeus 

ii) lineaarinen nopeus milloin tahansa.

Vastaukset:

Yo) Kulmanopeus on kulman asennon johdannainen: ω = φ '(t) = 2.

Toisin sanoen.

Ii) Auton lineaarinen nopeus on: V = R ・ ω = 2 M ・ 2 Rad/S = 4 m/s = 14,4 km/h

Harjoitus 3

Sama edellisen harjoituksen auto alkaa pysähtyä. Sen kulma -asema ajan funktiona annetaan seuraavalla lausekkeella:

φ (t) = 2 ・ t - 0,5 ・ t² 

Päättää:

i) kulmanopeus milloin tahansa

ii) lineaarinen nopeus milloin tahansa

iii) Aika, jonka otat pysähtyäksesi hetkestä, kun alat hidastaa

iv) Kulma kulki 

v) kulkiessa matkalla

Vastaukset:

Yo) Kulmanopeus on kulman asennon johdannainen: ω = φ '(t)

Ω (t) = φ '(t) = (2 ・ t - 0,5 ・ t²) '= 2 - t

Ii) Auton lineaarinen nopeus milloin tahansa antaa:

v (t) = r ・ ω (t) = 2 ・ (2 - t) = 4 - 2 t

Voi palvella sinua: Suhteellinen nopeus: käsite, esimerkit, harjoitukset

Iii) Aika, joka kuluu hetkeksi, jolloin se alkaa hidastua.

v (t) = 4 - 2 t = 0 => t = 2

Toisin sanoen se pysähtyy 2 s.

Iv) 2: n ajanjaksolla siitä lähtien, kun se alkaa pysähtyä, kunnes φ (2): n antama kulma kulkee:

φ (2) = 2 ・ 2 - 0,5 ・ 2^2 = 4 - 2 = 2 rad = 2 x 180 / π = 114,6 astetta

V) 2 sekunnin aikana ymmärretään, koska se alkaa pysähtyä, kunnes se pysäyttää etäisyyden, jonka on annettu:

S = r ・ φ = 2m ・ 2 rad = 4 m

Harjoitus 4

Auton pyörät ovat halkaisijaltaan 80 cm. Jos auto liikkuu nopeudella 100 km/h. Löydä: i) Pyörän kiertymisen kulmanopeus, ii) Pyörien kiertotaajuus, iii) Pyörän antamien kierrosten lukumäärä 1 tunnin reitillä.

Vastaukset:

Yo) Ensinnäkin käännämme Km/h a m/s -auton nopeuden

V = 100 km / h = (100/3.6) M/S = 27,78 m/s

Pyörien pyörimisnopeus annetaan:

Ω = v/r = (27,78 m/s)/(0,4 m) = 69,44 rad/s

Ii) Pyörän kiertotaajuus annetaan:

F = ω / 2π = (69,44 rad / s) / (2π rad) = 11,05 käännöstä / s

Kiertotaajuus ilmaistaan ​​yleensä kierroksina minuutissa r.p.m.

F = 11,05 käänny/s = 11,05 käännä/(1/60) min = 663,15 r.p.m

Iii)  Pyörän antamien käännösten lukumäärä 1 tunnin reitillä lasketaan tietäen, että 1 tunti = 60 minuuttia ja että taajuus on käännösten lukumäärä n jaettuna silloin, kun ne n annetaan.

F = n / t => n = f ・ t = 663,15 (käännökset / min) x 60 min = 39788,7 kierrosta.

Viitteet

1. Giancoli, D. Fysiikka. Periaatteet hakemuksissa. 6. painos. Prentice Hall. 106-108.
2. Resnick, r. (1999). Fyysinen. Osa 1. Kolmas painos espanjaksi. Meksiko. Mannertoimitusyhtiö S.-Lla. C: n.V. 67-69.
3. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Osa 1. Seitsemäs. Painos. Meksiko. Cengage Learning Editors. 84-85.
4. Geogebra.org