Areolaarinen nopeus miten se lasketaan ja ratkaistaan ​​harjoituksia

Se Areolaarinen nopeus Se on lakaisua aluetta kohti ja on vakio. Se on tyypillistä jokaiselle planeetalle ja syntyy Keplerin toisen lain kuvauksesta matemaattisella tavalla. Tässä artikkelissa selitämme, mistä se koostuu ja miten se lasketaan.

Puomi, joka edustaa aurinkokunnan ulkopuolella olevien planeettojen löytämistä, on aktivoinut kiinnostuksen planeettaliikkeeseen. Mikään ei usko, että nämä ekso-planeetit noudattavat muita lakeja kuin aurinkokunnan jo tunnetut ja kelvolliset.

Johannes Kepler oli tähtitieteilijä, joka ilman kaukoputken apua ja mentorinsa Tycho Brahen havaintojen avulla loi matemaattisen mallin, joka kuvaa planeettojen liikkumista auringon ympärillä.

Hän jätti tämän mallin, joka ilmaistaan ​​kolmessa laissa, jotka kantavat hänen nimensä ja jotka ovat edelleen voimassa kuin vuonna 1609, kun hän perusti kaksi ensimmäistä ja 1618, jolloin kolmas.

[TOC]

Kepler -lait

Nykyisellä kielellä Keplerin kolme lakia sanovat näin:

1. Kaikkien planeettojen kiertoradat ovat elliptisiä ja aurinko on keskittynyt.

2. Asentovektori, joka menee auringosta planeetalle, pyyhkäisee yhtä suuret alueet yhtäläisinä aikoina.

3. Planeetan kiertoratakauden neliö on verrannollinen kuvatun ellipsin puolikulmion kuutioon.

Planeetalla on lineaarinen nopeus, kuten mikä tahansa liikkuva tunnettu esine. Ja on enemmän: kun kirjoitat Keplerin toista lakia matemaattisessa muodossa, uusi käsite, nimeltään areolar Speed, tyypillinen jokaiselle planeetalle syntyy.

Miksi planeetat liikkuvat elliptisesti auringon ympäri?

Maa ja muut planeetat liikkuvat auringon ympäri, koska se kohdistaa voiman niihin: gravitaatiovetoisuus. Sama pätee mihin tahansa muuhun tähtiin ja järjestelmään mukautuviin planeetoihin, jos sinulla on niitä.

Se voi palvella sinua: herkkä lämpö: Konsepti, kaavat ja harjoitukset ratkaistu

Tämä on keskusvoima, joka tunnetaan nimellä keskusvoima. Paino on keskeinen voima, jonka kanssa kaikki ovat tuttuja. Kohde, joka käyttää keskusvoimaa, olipa se aurinko tai kaukainen tähti, houkuttelee planeettoja kohti keskustaan ​​ja he liikkuvat kuvaamalla suljettua käyrää.

Periaatteessa tätä käyrää voidaan arvioida kehäksi, kuten Nicolás Copernico, puolalainen tähtitieteilijä, joka on heliosentrisen teorian luoja, teki.

Vastuullinen voima on gravitaation vetovoima. Tämä voima riippuu suoraan tähden massoista ja kyseisestä planeetasta ja on käänteisesti verrannollinen niiden etäisyyden neliöön, joka erottaa ne.

Ongelma ei ole niin helppo, koska aurinkojärjestelmässä kaikki elementit ovat vuorovaikutuksessa tällä tavalla, lisäämällä asiaan monimutkaisuutta. Ne eivät myöskään ole hiukkasia, koska tähdet ja planeetat ovat mitattavissa.

Tästä syystä planeettojen kuljettaman kiertoradan tai piirin keskipiste ei ole tarkalleen keskittynyt tähtiin, vaan pisteeseen, joka tunnetaan nimellä Sol-Planet-järjestelmän painopiste.

Tuloksena oleva kiertorata on elliptinen. Seuraava kuva näyttää sen ottaen esimerkkinä maapallon ja auringon:

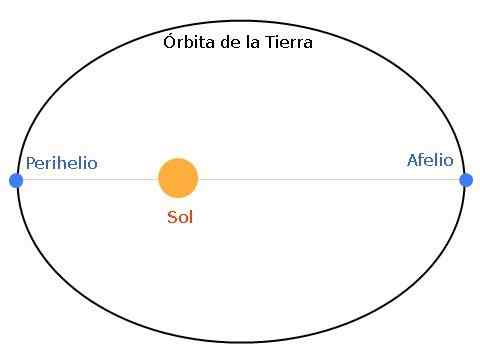Kuvio 1. Maan kiertoradalla on elliptinen, aurinko sijaitsee yhdessä polttoaineessa. Kun maa ja aurinko ovat suurimmalla etäisyydellä, sanotaan, että maa on apheliumissa. Ja jos etäisyys on minimaalinen, puhumme periheliosta.

Apellium on kauimpana sijainti maasta aurinkoon, kun taas perihelium on lähin kohta. Ellipsi voidaan olla enemmän tai vähemmän litistetä tähtijärjestelmän - planeetan ominaisuuksien mukaan.

ASELS- ja Perihelio -arvot vaihtelevat vuosittain, koska muut planeetat aiheuttavat häiriöitä. Muille planeetoille näitä tehtäviä kutsutaan tueksi ja asiantuntemukseksi.

Planeetan lineaarisen nopeuden suuruus ei ole vakio

Kepler havaitsi, että kun planeetta kiertää auringon ympäri, Barr -liikkeen aikana yhtä suuret alueet ovat yhtä suuret aikoina. Kuvio 2 näyttää graafisesti tämän merkityksen:

Se voi palvella sinua: mikä on hiukkasen tasapaino? (Esimerkkejä)Kuva 2. Planeetan sijaintivektori auringon suhteen on r. Kun planeetta kuvaa sen kiertorata kulkee ellipsiakaaria ΔS aikaan Δt.

Matemaattisesti se tosiasia₁ olla yhtä suuri kuin₂ Se ilmaistaan ​​näin:

Kaarireitit ovat pieniä, jotta kukin alue voi lähestyä kolmion reunoja:

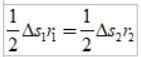
Kuten ΔS =vΔt, Missä V on planeetan lineaarinen nopeus tietyssä vaiheessa, vaihdettaessa meillä on:

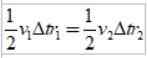
Ja koska aikaväli ΔT on sama, se saadaan:

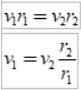
Kuten r₂ > r₁, Sitten v₁ > v₂, Toisin sanoen planeetan lineaarinen nopeus ei ole vakio. Itse asiassa maa menee nopeammin, kun se on periheliumissa kuin silloin, kun se on apheliumissa.

Siksi maan tai minkä tahansa planeetan lineaarinen nopeus auringon ympärillä ei ole suuruus, joka auttaa karakterisoimaan mainitun planeetan liikettä.

Areolaarinen nopeus

Keplerin toinen laki ehdottaa uutta suuruutta, jota kutsutaan areolaariseksi nopeudeksi. Se määritellään alueen pyyhkäisyn ajan ja on vakiona. Sen laskemiseksi käytetään seuraavaa kuvaa:

Kuva 3. Maan sijaintivektori (tai planeetta) auringon suhteen on r, ja liikkuessa maa kokee siirtymän, myös vektori ΔR.

Pieni maapallon pyyhkäisy alue valitaan suoritettaessa sen elliptistä piiriä, jonka merkitsemme kuinka ΔA. Tätä varten tarvittava aika on Δt.

Kuvio 3 esittää maan sijaintivektorin auringon suhteen, merkitty r: llä. Kun maa liikkuu, koe siirtymä ΔR.

Tämä alue vastaa puolta kuvassa 3 esitetystä suorakulmion alueesta:

Määrä ΔR/ΔT on juuri maan lineaarinen nopeus, joten areolaarinen nopeus pysyy:

V_-Lla Kansainvälisessä järjestelmässä he ovat:

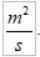
Huomaa, että vaikka sekä R että V vaihtelevat, tuote pysyy vakiona. Tämä muuttuu areolaarinen nopeus erittäin sopivaksi suuruudeksi karakterisoidakseen planeetan liikkeen tähden ympärillä.

Voi palvella sinua: Antoine -vakiot: kaavat, yhtälöt, esimerkit

R: n ja V: n tuote on kulman momentin l suuruus, jotta areolaarinen nopeus voidaan ilmaista seuraavasti:

Laskemalla lineaarinen nopeus ja areolaarinen nopeus

Seuraavalla esimerkillä osoitamme, kuinka laskea areolaarinen nopeus, kun jotkut planeettaliikkeen parametrit tunnetaan:

Harjoittele

Keplerin lakien mukaan ekso-planetti liikkuu auringonsa ympäri elliptisen kiertoradan jälkeen. Kun se on Expertrossa, sen radiovektori on r₁ = 4 · 10⁷ km, ja kun se on tuessa, on r₂ = 15 · 10⁷ km. Lineaarinen nopeus sen asiantuntemuksessa on V₁ = 1000 km/s.

Laskea:

A) tuen nopeuden suuruus.

B) Exo-planetin areolaarinen nopeus.

C) Ellipsen suuren puoliakselin pituus.

Vastaa)

Yhtälöä käytetään:

jossa numeeriset arvot korvataan.

Jokainen termi tunnistetaan seuraavasti:

v₁ = Nopeus tuen; v₂ = Nopeus asiantuntijassa; r₁= Kirjoittajan etäisyys,

r -₂= Etäisyys asiantuntijasta.

Näiden arvojen kanssa se on saatu:

Vastaus b)

Käytettävä yhtälö on

jossa pari arvoa R ja V V on korvata, koska V_-Lla Se on vakio planeetta:

Vastaus c)

Ellipsin tärkeimmän puoliakselin pituus on Semi -Semi -Semi -Semi -Semi -seismum ja asiantuntemus:

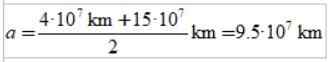
Bibliografia

1. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Osa 1. Meksiko. Cengage Learning Editors. 367-372.
2. Stern, D. (2005). Planeettaliikkeen kolme Kepler -lakia. Haettu PWG: stä.GSFC.potti.Hallitus
3. HUOMAUTUS: Ehdotettu harjoitus tehtiin ja muutettiin McGrawhill -kirjan seuraavasta tekstistä. Valitettavasti se on PDF -muodossa eristetty luku, ilman otsikkoa tai tekijää: MHEDUCATION.ES/BCV/Guide/Luku/844817027x.Pdf