Keskimääräiset nopeuskaavat, miten se lasketaan ja ratkaistu harjoittelu

Se keskinopeus Siirrettävälle hiukkaselle se määritellään syyksi hänen kokemuksensa variaation ja muutoksen käytetyn aikavälin välillä. Yksinkertaisin tilanne on sellainen, jossa hiukkas liikkuu X -akselin edustamaa suoraa linjaa pitkin.

Oletetaan₁ ja x₂ Aikoina t₁ ja T₂ vastaavasti. Keskimääräisen nopeuden määritelmä v_m Se on matemaattisesti esitetty seuraavasti:

Yksiköt v_m Kansainvälisessä järjestelmässä ne ovat metrejä/toinen (m/s). Muut yleiset käyttöyksiköt, jotka ilmestyvät mobiilitekstiin ja laitteisiin.

Kreikkalainen kirjain "Δ" lukee "Delta" ja sitä käytetään yhteenvetoon kahden määrän välisestä erosta.

[TOC]

Keskimääräisen nopeuden vektorin V -ominaisuudet V_m

Keskimääräinen nopeus on tärkeä liikkeelle. Lähde: Pixabay

Keskimääräinen nopeus on vektori, koska se liittyy sijainnin muutokseen, joka puolestaan ​​tunnetaan nimellä Vektorin siirtymä.

Tätä laatua edustaa lihavoitu tai nuoli, joka osoittaa suuruuden. Mitossa ainoa mahdollinen suunta on X -akselin suunta, ja siksi se voidaan antaa vektorimerkinnällä.

Koska vektoreilla on suuruus, suunta ja merkitys, alkuperäinen silmämäärä yhtälöön osoittaa, että keskimääräisellä nopeudella on sama suunta ja järki kuin siirtymällä.

Kuvittele esimerkin hiukkaset, jotka liikkuvat suoraa linjaa pitkin. Liikesi kuvaamiseksi on välttämätöntä osoittaa vertailupiste, joka on "alkuperä" ja merkitään nimellä tai.

Hiukkas voi liikkua pois tai lähestyä tai joko vasemmalle tai oikealle. Voit myös käyttää paljon tai vähän aikaa tiettyyn sijaintiin.

Se voi palvella sinua: Lämpö: Kaavat ja yksiköt, ominaisuudet, miten se mitataan, esimerkkejä

Mainitut suuruudet: sijainti, siirtymä, ajanjakso ja keskimääräinen nopeus kuvaavat hiukkasen käyttäytymistä liikkuessa. Kyse on suuruudesta Kinemaattinen.

Käytetään käyttävien ja merkin (-) sijaintien tai paikkojen vasemmalle tai merkin (+) erottamiseksi (+).

Keskimääräisellä nopeudella on geometrinen tulkinta, joka voidaan nähdä seuraavassa kuvassa. P- ja Q -pisteiden läpi kulkevan linjan kaltevuus. Kun leikkaat asentoon ja asentoon. Aika kahdessa pisteessä, se on linja kuivuminen.

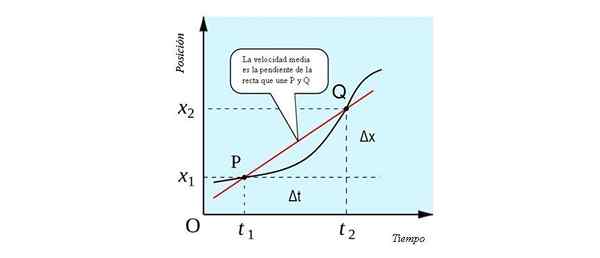Keskimääräisen nopeuden geometrinen tulkinta P- ja Q -pisteisiin liittyvän linjan kaltevuutena. Lähde: すじにく シチュー [CC0].

Keskimääräisen nopeuden merkit

Seuraavalle analyysille on otettava huomioon se t₂ t₁. Eli seuraava hetki on aina suurempi kuin virta. Tällä tavalla t₂ - t₁ Se on aina positiivinen, mikä yleensä on järkevää päivittäin.

Silloin keskimääräisen nopeuden merkki määritetään x₂ - x₁. Huomaa, että se on tärkeää.

Tai "eteenpäin" tai "takaisin", kuten lukija suosii.

Jos keskimääräinen nopeus on positiivinen, se tarkoittaa sitä keskimäärin arvo "x”Kasvaa ajan myötä, vaikka tämä ei tarkoita, että se olisi voinut vähentyä jossain vaiheessa tarkasteltavana ajankohtana - Δt -.

Kuitenkin globaalisti, ajan lopussa Δt, Hän päättyi suurempaan asemaan kuin se, joka hänellä oli alussa. Liikkeen yksityiskohdat jätetään huomiotta tässä analyysissä.

Voit palvella sinua: Newtonin kolmas laki: sovellukset, kokeet ja harjoitukset

Entä jos keskimääräinen nopeus on negatiivinen? No, se tarkoittaa, että hiukkas päättyy pienemmällä koordinaatilla kuin se, jonka kanssa se alkoi. Groso -tila siirtyi taaksepäin. Katsotaanpa joitain numeerisia esimerkkejä:

Esimerkki 1: Ottaen huomioon ilmoitetut alkuperäiset ja lopulliset sijainnit, ilmoita keskimääräisen nopeuden merkki. Missä hiukkas liikkui maailmanlaajuisesti?

a) x₁ = 3 m; x₂ = 8 m

Vastaus: x₂- x₁  = 8 m - 3 m = 5 m. Positiivinen keskimääräinen nopeus, hiukkas eteni eteenpäin.

b) x₁ = 2 m; x₂ = -3 m

Vastaus- x₂ - x₁ = -3 m -2 m = -5 m. Keskimääräinen negatiivinen nopeus, hiukkas siirtyi taaksepäin.

 c) x₁  = - 5 m; x₂ = -12 m

Vastaus: x₂ - x₁   = -12 m -( -5 m) = -7 m. Keskimääräinen negatiivinen nopeus, hiukkas siirtyi taaksepäin.

d) x₁  = - 4 m; x₂ = 10 m

Vastaus: x₂ - x₁  = 10 m - (-4m) = 14 m. Positiivinen keskimääräinen nopeus, hiukkas eteni eteenpäin.

Voiko keskimääräinen nopeus olla 0? Joo. Niin kauan kuin lähtökohta ja saapumispiste ovat samat. Tarkoittaako tämä, että hiukkas oli välttämättä levossa koko ajan?

Ei, se tarkoittaa vain, että matka oli edestakainen matka. Ehkä hän matkusti nopeasti tai ehkä hyvin hitaasti. Toistaiseksi sitä ei tunneta.

Keskimääräinen nopeus: skalaarinen suuruus

Tämä saa meidät määrittelemään uuden termin: Keskinopeus. Fysiikassa on tärkeää erottaa vektorialueet ja suuruudet, jotka eivät ole: skalaarit.

Hiukkaselle, joka teki edestakaisen matkan, keskimääräinen nopeus on 0, mutta se olisi voinut olla erittäin nopea tai ehkä ei. Tietääksesi sen, keskimääräinen nopeus määritellään seuraavasti:

Keskimääräisen nopeuden yksiköt ovat samat kuin keskimääräisen nopeuden yksiköt. Perusero molempien suuruuksien välillä on, että keskimääräinen nopeus sisältää mielenkiintoista tietoa hiukkasen suunnasta ja suunnasta.

Se voi palvella sinua: fermioninen kondensaatti: Ominaisuudet, sovellukset ja esimerkit

Toisaalta keskimääräinen nopeus tarjoaa vain numeerista tietoa. Hänen kanssaan tiedetään, kuinka nopeasti tai hidasta hiukkasa liikkui, mutta ei, jos hän teki sen eteenpäin tai taaksepäin. Siksi se on skalaarinen suuruus. Kuinka erottaa heidät merkitsemään heitä? Yksi tapa on jättää rohkea vektorille tai nuolen asettaminen.

Ja on tärkeää huomata, että keskimääräisen nopeuden ei tarvitse olla yhtä suuri kuin keskimääräinen nopeus. Edestakaisella matkalla keskimääräinen nopeus on nolla, mutta keskimääräinen nopeus ei. Molemmilla on sama numeerinen arvo, kun matkustat aina samaan suuntaan.

Liikuntaa

Olet palannut kotiin koulusta hiljaa nopeudella 95 km/h/130 km. Aloita sade ja vähentää nopeutta 65 km/h. Hän saa lopulta kotiin ajamisen jälkeen 3 tuntia ja 20 minuuttia.

a) Kuinka pitkälle koulukunnasi on?

b) mikä oli keskimääräinen nopeus?

Vastaukset:

a) Jotkut aiemmat laskelmat ovat välttämättömiä:

Matka on jaettu kahteen osaan, kokonaisetäisyys on:

D = d1+ d₂, D1 = 130 km: n kanssa

Kokonaisaika on 3 tuntia ja 20 minuuttia = 3 + 1/3 tuntia = 10/3 tuntia = 3.33 tuntia (on tarpeen sijoittaa samat yksiköt ajaksi, tässä tapauksessa se on tarkoituksenmukaista).

T2 = 3.33 - 1.37 tuntia = 1.96 tuntia

D: n laskenta_2:

d -d₂ = 65 km/h x 1.96 H = 125. 4 km.

Koulu on D1+ D₂ = 255.4 km päässä talosta.

b) Nyt löydät keskimääräisen nopeuden:

Viitteet

1. Giancoli, D. Fysiikka. Periaatteet hakemuksissa. Kuudes painos. Prentice Hall. 21-22.
2. Resnick, r. (1999). Fyysinen. Osa 1. Kolmas painos espanjaksi. Meksiko. Mannertoimitusyhtiö S.-Lla. C: n.V. 20-21.
3. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Osa 1. 7mehu. Painos. Meksiko. Cengage Learning Editors. 21-23.