Molaarinen tilavuuskonsepti ja kaava, laskenta ja esimerkit

Hän molaarinen tilavuus Se on intensiivinen ominaisuus, joka osoittaa, kuinka paljon tilaa määrityksen tai yhdisteen mooli miehittää. Edustaa symbolia V_m, ja ilmaistaan ​​DM -yksiköissä³/mol kaasuille ja cm³/Mol nesteille ja kiinteille aineille, koska jälkimmäiset rajoittuvat enemmän niiden suurimpiin molekyylien välisiin voimiin.

Tämä ominaisuus toistuu tutkiessaan termodynaamisia järjestelmiä, joihin liittyy kaasuja; koska nesteiden ja kiinteiden aineiden osalta yhtälöt määrittävät V_m Heistä tulee monimutkaisempia ja epätarkempia. Siksi peruskurssien suhteen molaarinen tilavuus liittyy aina ihanteelliseen kaasuteoriaan.

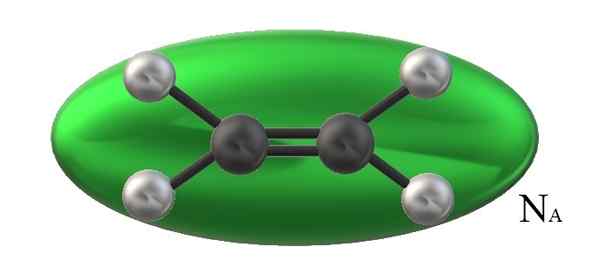
Eteenimolekyylin tilavuutta rajoittaa pinnallisesti vihreä ellipsoidi ja Avogadro -aikojen lukumäärä tämä määrä. Lähde: Gabriel Bolívar.

Tämä johtuu siitä, että ihanteellisissa tai täydellisissä kaasuissa rakenteellisilla näkökohdilla ei ole merkitystä; Kaikki sen hiukkaset visualisoidaan palloiksi, jotka törmäävät elastisesti keskenään ja käyttäytyvät samalla tavalla riippumatta siitä, mitkä niiden massansa tai ominaisuudet ovat.

Siten yksi ihanteellisen kaasun mooli miehittää tietyssä paineessa ja lämpötilassa samalla tilavuudella V_m. Sanotaan. Tämä arvo on hyödyllinen ja likimääräinen, vaikka todelliset kaasut arvioidaan.

[TOC]

Käsite ja kaava

Kaasuihin

Välitön kaava lajin molaarisen määrän laskemiseksi on:

V_m = V/n

Missä v on sen käyttämä tilavuus ja n Lajien määrä moolissa. Ongelmana on, että v_m Se riippuu molekyylien kokemasta paineesta ja lämpötilasta, ja matemaattisen ekspression halutaan ottaa nämä muuttujat huomioon.

Voi palvella sinua: molealiteetti

Kuvan etyleeni, h₂C = ch₂, Siinä on molekyylitilavuus, johon liittyy vihreä ellipsoidi. Tämä h₂C = ch₂ Se voi pyöriä monin tavoin, mikä on kuin se, että se liikkui tilassa, sanoi ellipsoidia visualisoidakseen kuinka paljon äänenvoimakkuutta se miehittää (ilmeisesti halveksittava).

Kuitenkin, jos tällaisen vihreän ellipsoidin tilavuus kertoo sen n_-Lla, Avogadro -numerossa on sitten mooli eteenimolekyylejä; Yksi mol ellipsoidia vuorovaikutuksessa toistensa kanssa. Korkeammassa lämpötilassa molekyylit erottuvat toisistaan; Vaikka ne ovat suuressa paineessa, he supistuvat ja vähentävät määränsä.

Siksi v_m on riippuvainen p: stä ja t: stä. Etyleeni on tasainen geometria, joten ei voida ajatella, että sen V_m Ole tarkka ja täsmälleen sama kuin metaani, Cho₄, tetraedrinen geometria ja kykenevä edustamaan palloa eikä ellipsoidia.

Nesteille ja kiinteille aineille

Nesteiden ja kiinteiden aineiden molekyyleillä tai atomilla on myös oma V_m, joka voi liittyä tiheyteen:

V_m = m/(d · n)

Lämpötila vaikuttaa molaaritilavuuteen enemmän nesteissä ja kiinteissä aineissa kuin paine, kunhan jälkimmäinen ei vaihtele voimakkaasti tai kohtuuttomia (GPA: n luokassa). Samoin, kuten etyleenillä mainittiin, geometriat ja molekyylirakenteet vaikuttavat suuresti V: n arvoihin_m.

Normaaliolosuhteissa havaitaan kuitenkin, että eri nesteiden tai kiinteiden aineiden tiheydet eivät vaihtele liikaa niiden voimakkuutta; Sama koskee sen molaarisia määriä. Huomaa, että tiheimmät ne ovat, alempi V_m.

Kiinteän aineesta sen molaarinen tilavuus riippuu myös sen kiteisistä rakenteista (sen yksikkösolun tilavuus).

Voi palvella sinua: kaliumbiftalaatti: rakenne, nimikkeistö, käyttö, riskit

Kuinka laskea molaarinen tilavuus?

Toisin kuin nesteet ja kiinteät aineet, ihanteellisissa kaasuissa on yhtälö, jonka avulla voit laskea V_m riippuen p ja t ja sen muutokset; Tämä on ihanteelliset kaasut:

P = nrt/v

Joka sopii ilmaisemaan V/n:

V/n = rt/p

V_m = Rt/p

Jos käytämme kaasuvakiota r = 0,082 l · atm · k^-1· Mol^-1, Sitten lämpötilat on ilmaistava Kelvinissä (K) ja ilmakehän paineet. Huomaa, että tässä havaitaan miksi v_m Se on intensiivinen omaisuus: T: llä ja P ei ole mitään tekemistä kaasun massan kanssa, mutta sen tilavuudella.

Nämä laskelmat ovat päteviä vain olosuhteissa, joissa kaasut käyttäytyvät tiiviisti ihanteellisuuteen. Kokeilun kautta saatuilla arvoilla on kuitenkin pieni marginaali suhteessa teoreetikkoihin.

Molaarisen tilavuuden laskentaesimerkit

Esimerkki 1

Sinulla on kaasu ja jonka tiheys on 8,5,5 · 10^-4 g/cm³. Jos sinulla on 16 grammaa, mikä vastaa 0,92 moolia y, laske molaarinen tilavuus.

Tiheyskaavasta voimme laskea, mikä tilavuus ja käyttää sellaisia ​​16 grammaa:

V = 16 g/ (8,5 · 10^-4 g/cm³-A

= 18.823,52 cm³ tai 18,82 l

Niin v_m Se lasketaan suoraan jakamalla tämä tilavuus annettujen moolien määrän välillä:

V_m = 18,82 l/0,92 mol

= 20,45 l/mol o l · mol^-1 tai DM³· Mol^-1

Harjoitus 2

Edellisessä esimerkissä ja sitä ei määritetty milloin tahansa, mikä oli mainitun kaasun hiukkaset, jotka olivat kokeneet. Olettaen, että se toimi ja ilmakehän paineessa ja siinä, laske sen puristamiseksi määritettyyn molaaritilavuuteen tarvittava lämpötila.

Voi palvella sinua: pakkauskerroin

Harjoituslausunto on pidempi kuin sen päätöslauselma. Käännymme yhtälöön:

V_m = Rt/p

Mutta selvitämme t, ja tiedämme, että ilmakehän paine on 1 atm, ratkaisemme:

T = v_mPR

= (20,45 l/mol) (1 atm)/(0,082 L · atm/k · mol)

= 249,39 K

Eli yksi mooli ja vie 20,45 litraa lämpötilassa, joka on lähellä -23,76 ºC.

Harjoitus 3

Yllä olevien tulosten jälkeen määritä V_m 0 ºC: ssa, 25 ° C ja absoluuttisessa nollassa ilmakehän paineessa.

Muuttaa lämpötilat Kelviniksi, meillä on ensimmäinen 273,17 K, 298,15 K ja 0 K. Ratkaisemme suoraan korvaamalla ensimmäisen ja toisen lämpötilan:

V_m = Rt/p

= (0,082 L · atm/ k · mol) (273,15 K)/ 1 atm

= 22,40 l/mol (0 ºC)

= (0,082 L · atm/ k · mol) (298,15 K)/ 1 atm

= 24,45 l/mol (25ºC)

Alussa mainittiin 22,4 litran arvo. Huomaa kuinka v_m nousta lämpötilan kanssa. Kun haluat tehdä saman laskelman absoluuttisella nollalla, kompastumme termodynamiikan kolmanteen lakiin:

(0,082 L · atm/ k · mol) (0 K)/ 1 atm

= 0 l/mol (-273,15 ºC)

Kaasua eikä sillä ole olemassa olevaa molaarista tilavuutta; Tämä tarkoittaa, että siitä on tullut neste ja edellinen yhtälö ei ole enää voimassa.

Toisaalta V: n mahdottomuus V: n laskemiseen_m Absoluuttisessa nolla ei noudata termodynamiikan kolmatta lakia, jonka mukaan mitään aineita on mahdotonta jäähdyttää absoluuttisen nollan lämpötilassa.

Viitteet

1. Iranin. Levine. (2014). Fysikaalis -periaatteet. Kuudes painos. MC Graw Hill.
2. Glassi. (1970). Fysikaaliset kemian sopimus. Toinen painos. Aguilar.
3. Wikipedia. (2019). Molaarinen tilavuus. Haettu: vuonna.Wikipedia.org
4. Helmestine, Anne Marie, PH.D -d. (8. elokuuta 2019). Molaarisen tilavuuden määritelmä kemiassa. Toipunut: Admingco.com
5. Byju. (2019). Molaarinen tilavuuskaava. Toipunut: byjus.com
6. González Mónica. (28. lokakuuta 2010). Molaarinen tilavuus. Palautettu: kemia.Laguia2000.com