Chi-neliö (χ²) jakauma, miten se lasketaan, esimerkkejä

Todiste Chi -neliö jompikumpi ji-neliö (χ², Missä χ on kreikkalainen kirjain, nimeltään "chi"), käytetään tietyn muuttujan käyttäytymisen määrittämiseen, ja myös kun haluat tietää, ovatko kaksi vai useampia muuttujia tilastollisesti riippumattomia.

Muuttujan käyttäytymisen tarkistamiseksi testi, jota kutsutaan Chi -neliötesti säätö. Tietää, onko kaksi tai useampaa muuttujaa tilastollisesti riippumaton testistä Chi itsenäisyyden aukio, kutsutaan myös varovainen.

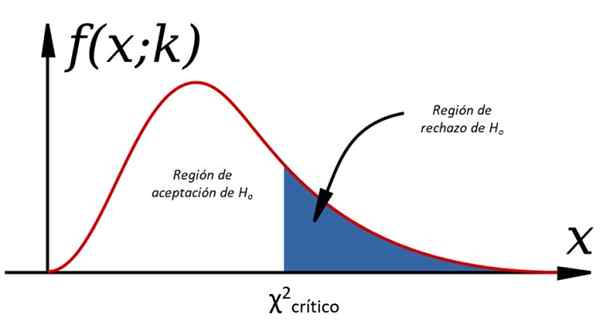
Kuvio 1. Hypoteesitestit Chi Cuadradon kautta

Nämä todisteet ovat osa päätöksentekoa koskevaa tilastollista teoriaa, jossa tutkitaan populaatiota ja siitä tehdään päätöksiä, analysoimalla yksi tai useita siitä otettu näytteitä. Tätä varten on välttämätöntä tehdä tiettyjä muuttujia koskevia oletuksia hypoteesi, joka voi olla varma tai ei ole varma.

On joitain testejä näiden oletusten kontrastiksi ja määrittämiseksi, mikä on pätevä, tietyssä luottamusmarginaalissa, mukaan lukien chi-neliötesti, jota voidaan käyttää kahden ja useimpien populaatioiden vertaamiseen.

Kuten näemme, tarkastellaan yleensä kahden tyyppistä hypoteesia joistakin populaatioparametrista kahdessa näytteessä: NULL -hypoteesi, nimeltään H_jompikumpi (Näytteet ovat riippumattomia), ja vaihtoehtoinen hypoteesi, merkitty h: ksi₁, (näytteet korreloivat), mikä on sen vastaista.

[TOC]

Milloin käytetään chi-neliötestiä?

Chi -neliötesti sovelletaan muuttujiin, jotka kuvaavat ominaisuuksia, kuten sukupuoli, siviiliasema, veriryhmä, silmien väri ja erityyppiset mieltymykset.

Testi on suunniteltu haluamallasi tavalla:

-Tarkista, onko jakauma sopiva muuttujan kuvaamiseen, jota kutsutaan hyvyyden säätäminen. CHI -neliötestin kautta voit tietää, onko valittujen teoreettisen jakauman ja havaitun taajuuden jakauman välillä merkittäviä eroja.

-Tiedä, ovatko kaksi X- ja Y -muuttujaa riippumattomia tilastollisesta näkökulmasta. Tämä tunnetaan nimellä Itsenäisyystesti.

Koska se koskee laadullisia tai kategorisia muuttujia, Chi -neliötestiä käytetään laajasti yhteiskuntatieteissä, hallinnossa ja lääketieteessä.

Edellytykset sen soveltamiseksi

Sen oikein soveltamiseksi on kaksi tärkeää vaatimusta:

Se voi palvella sinua: mikä on Rhombus -alueen ja suorakulmion välinen suhde?

-Tiedot on ryhmitelty taajuuksille.

-Näytteen on oltava riittävän suuri, jotta Chi -neliöjakauma on voimassa, muuten sen arvo on yliarvioitu ja aiheuttaa nollahypoteesin hylkäämisen, kun sen ei pitäisi olla niin.

Yleinen sääntö on, että jos ryhmiteltyissä tiedoissa on taajuus, jonka arvo on alle 5, sitä ei käytetä. Jos taajuus on enemmän kuin 5, niin ne on yhdistettävä yhdessä, jotta saadaan taajuus, jonka numeerinen arvo on suurempi kuin 5.

Chi -neliöjakauma

χ² Se on jatkuva todennäköisyyksien jakautuminen. Parametrista riippuen on todella erilaisia ​​käyriä k -k - nimeltään vapauden asteet satunnaisesti.

Sen ominaisuudet ovat:

-Käyrän alla oleva alue on yhtä suuri kuin 1.

-Χ -arvot² Ne ovat positiivisia.

-Jakelu on epäsymmetristä, toisin sanoen siinä on puolueellisuus.

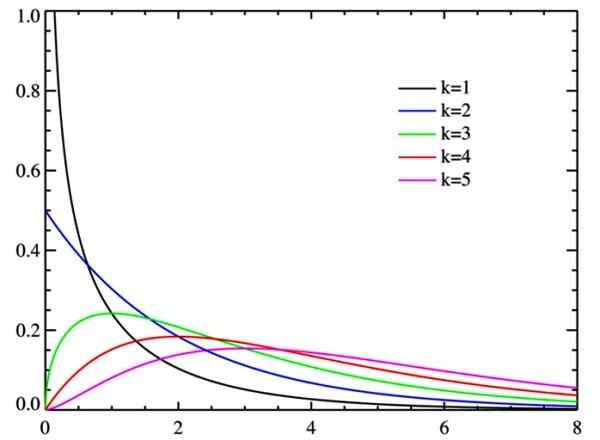Kuva 2. Chi -neliöjakauma wattien vapausasteille. Lähde: Wikimedia Commons.

Vapauden asteet

Kun vapausasteet kasvavat, chi-neliöjakauma on yleensä normaalia, kuten kuvassa voidaan nähdä.

Tietylle jakautumiselle vapausasteet määritetään varataulukko, joka on taulukko, jossa muuttujien havaitut taajuudet tallennetaan.

Jos taulukossa on F rivit ja c sarakkeet, k -k - On:

K = (f - 1) ⋅ (c - 1)

Hypoteesin formulaatio

Kun Chi -neliötesti on säätö, seuraavat hypoteesit on muotoiltu:

-H_jompikumpi: Muuttuja X: llä on todennäköisyysjakauma F (x) erityisillä parametreilla ja₁, ja₂…, Ja_p

-H₁: X: llä on toinen todennäköisyysjakauma.

Nollahypoteesissa oletettu todennäköisyysjakauma voi olla esimerkiksi hyvin tunnettu normaali jakauma, ja parametrit olisivat keskimääräinen μ ja keskihajonta σ.

Lisäksi nollahypoteesia arvioidaan tietyllä merkitsevyystasolla, ts.

Yleensä tämä taso on osoitettu 1 %, 5 % tai 10 % ja mitä alhaisempi testitulos, sitä luotettavampi.

Voi palvella sinua: Mumm

Ja jos käytetään CHI -neliötestiä varautumistestiä, kuten kuten olemme sanoneet, tarkistaa kahden muuttujan X ja Y: n välinen riippumattomuus, hypoteesit ovat:

-H_jompikumpi: Muuttujat x ja y ovat riippumattomia.

-H₁: X ja y ovat riippuvaisia.

Jälleen on tarpeen määritellä merkitsevyystaso tietää virheen mittaaminen päätöksenteossa.

Kuinka chi-neliötilastot lasketaan?

Chi -neliötilastot lasketaan seuraavasti:

Symboli ∑ tarkoittaa "summausta", joka meidän on tehtävä ilmoitetusta murto -osuudesta.

Summa suoritetaan ensimmäisestä luokasta I = 1 viimeiseen, mikä on I = k.

Sitä paitsi:

-F_jompikumpi Se on havaittu taajuus (se tulee saatuista tiedoista).

-F_ja Se on odotettu tai teoreettinen taajuus (on tarpeen laskea se tiedoista).

Nullihypoteesin hyväksymiseksi tai hylkäämiseksi χ lasketaan² Havaittujen tietojen osalta ja verrataan nimeltään arvoon Chi Critical Square, joka riippuu vapauden asteista k -k - ja merkityksen taso α-

χ²_kriittinen =  χ²_{K, α}

Jos haluamme esimerkiksi suorittaa testin merkitsevyystasolla 1 %, niin α = 0.01, jos se tapahtuu 5%: lla, α = 0.05 ja niin edelleen. P, jakeluparametri, kuten:

P = 1 - α

Nämä kriittiset neliöarvot määritetään taulukolla, jotka sisältävät kertyneen alueen arvon. Esimerkiksi k = 1: lle, joka edustaa yhtä vapausastetta ja α = 0.05, vastaa p = 1-.05 = 0.95, arvo χ² Se on 3.841.

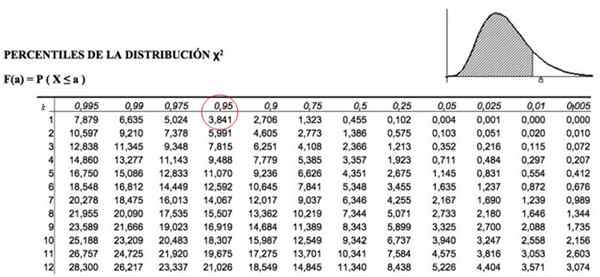Kuva 3. Chi -neliöjakauma -arvotaulukko. Lähde: f. Zapata.

AC: n hyväksymiskriteerit_jompikumpi

H -hyväksymiskriteerit_jompikumpi On:

-Kyllä χ² < χ²_kriittinen  H_jompikumpi, muuten se hylätään (katso kuva 1).

Esimerkki laskennasta

Seuraavassa sovelluksessa CHI -neliötestiä käytetään itsenäisyystestinä.

Oletetaan, että tutkijat haluavat tietää, liittyykö musta kahvin mieltymys henkilön genreen, ja määrittelevät vastauksen α = 0: n merkitsevyystasolla.05.

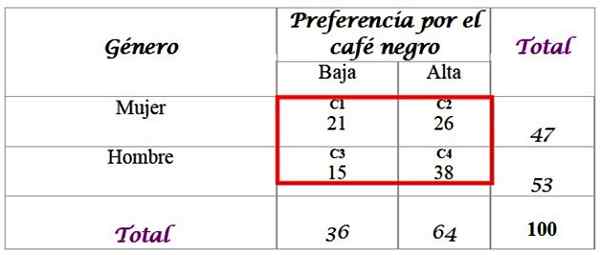
Voi palvella sinua: Ulkoiset vaihtoehtoiset kulmat: RAKENNUKSET JA TAKAUTUKSET

Tätä varten 100 haastatellun ihmisen näyte ja heidän vastauksensa on saatavana:

Vaihe 1

Luo hypoteesit:

-H_jompikumpi: Sukupuoli ja mustan kahvin suosiminen ovat riippumattomia.
-H₁: Musta kahvin maku liittyy henkilön genreen.

Vaihe 2

Laske odotetut jakelutaajuudet, joille vaaditaan viimeisen rivin kokonais. Jokaisella punaisen ruudun solulla on odotettu arvo F_ja, joka lasketaan kertomalla sen R -rivin F kokonaismäärä kokonaissarakkeella C, jaettuna kokonaisnäytteellä n:

F_ja = (F x c) /n

Tulokset ovat seuraavat jokaiselle solulle:

-C1: (36 x 47) / 100 = 16.92
-C2: (64 x 47) / 100 = 30.08
-C3: (36 x 53) / 100 = 19.08
-C4: (64 x 53) / 100 = 33.92

Vaihe 3

Sitten sinun on laskettava Chi Cuadrado -tilastot tälle jakaumalle, annetun kaavan mukaan:

χ²= [(21 - 16.92)² ÷ 16. 92] + [(26 - 30.08)² ÷ 30.08] + [(15 - 19.08)² ÷ 19.08]+ [(38 - 33.92)² ÷ 33. 92] = 0.9838 + 0.5534 + 0.8725 + 0.4908 = 2.9005

Vaihe 4

Määritä χ²_kriittinen, Tietäen, että rekisteröidyt tiedot ovat f = 2 riviä ja c = 2 saraketta, siksi vapausasteiden lukumäärä on:

K = (2-1) ⋅ (2-1) = 1.

Mikä tarkoittaa, että meidän on katsottava taulukossa, joka on esitetty yläpuolella χ²_{K, α} = χ²_{1; 0 -.05} , mikä on:

χ²_kriittinen = 3.841

Vaihe 5

Vertaa arvoja ja päätä:

χ² = 2.9005

χ²_kriittinen = 3.841

Koska χ² < χ²_kriittinen Nollahypoteesi hyväksytään ja päätellään, että mustan kahvin suosiminen ei liity henkilön genreen, merkitsevyystaso on 5%.

Viitteet

1. Chi -neliötesti itsenäisyyden vuoksi. Toipunut: Saylordotorg.Github.Io.
2. Med -aalto. Terveystieteisiin sovelletut tilastot: Ji-neliötesti. Toipunut: Medwave.Cl.
3. Todennäköisyydet ja tilastot. Shi Square Säätö hyvyystesti. Haettu: Todennäköisyys-.com.
4. Triola, m. 2012. Perustilastot. 11. päivä. Painos. Addison Wesley.
5. Yksinäinen. Chi -neliötesti. Toipunut: Neuvonta.Cuautitlan2.Yksinäinen.MX.