Lineaarisen momentiaperiaate, esimerkit, harjoitukset.

Se lineaarisen vauhdin säilyttäminen kehon osalta osoittaa, että sen massatuote nopeudella vektori on vakio määrä, kun kehossa ei ole vuorovaikutusta muiden kappaleiden kanssa ja nopeudella mitattuna kiinteän tai ei-akuutin vertailujärjestelmän suhteen.

Kun on olemassa useita runkoja, jotka ovat vuorovaikutuksessa vain niiden välillä, mutta ei ulkoajan kanssa, niin lineaarinen liikemäärä sarjasta pysyy myös vakiona ajan myötä.

Avaruuden astronautti on vapaa kaikesta vuorovaikutuksesta, joten sen lineaarinen hetki

Lineaarinen hetki, lineaarisen liikkeen määrä tai yksinkertaisesti vauhti, Se on merkitty kirjaimella p Ja se on vektorimääräinen määrä:

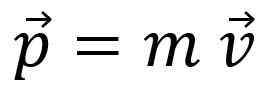
Lineaarinen hetki ei ole sama kuin nopeus, vaikka suhde on ilmeinen: esimerkiksi kuorma -autolla, joka menee 20 km/h, on enemmän lineaarista aikaa kuin samalla nopeudella liikkuvalla polkupyörällä.

Jotta kehon lineaarinen momentti muuttuu, on välttämätöntä, että ulkoinen nettovoima vaikuttaa siihen, muuten se pysyy vakiona. Lisäksi lineaarinen hetki P järjestelmän muodostama N-vartalo Se on yksittäisten hetkien vektorisumma:

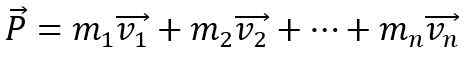
[TOC]

Lineaarisen liikkeen määrän säilyttämisperiaate

Kehossa, joka ei ole voimia (tai sellainen, jossa kaikki sen voimat peruutetaan) tapahtuu, että lineaarinen hetki.

Samalla tavalla se kulkee järjestelmässä, jonka muodostavat useat rungot, jotka ovat vain vuorovaikutuksessa keskenään, mutta ei ulkoisen ympäristön kanssa: järjestelmän kokonaismomentti pysyy kiinteänä sarjan evoluution aikana.

Tämä säilyttämisperiaate on mainittu näin:

N-rungon kokonaismomentti, joka on vain vuorovaikutuksessa toistensa kanssa, mutta ei ulkoympäristön kanssa, on muuttumaton määrä ajassa.

Ja matemaattisesti se ilmaistaan ​​seuraavasti:

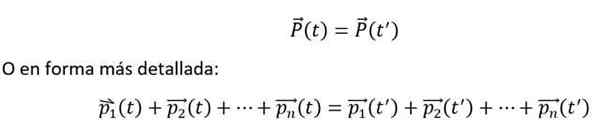
Aikaisempi tasa -arvo toteutetaan, jos ja vain jos n-Rungot ovat vuorovaikutuksessa keskenään, mutta eivät ulkoympäristön kanssa. Lisäksi yksittäiset hetket tulisi aina mitata inertiaalisen vertailujärjestelmän suhteen.

Esimerkit

Esimerkki 1

Avaruudessa kaksi astronauttia otetaan käsistä ja pysyvät kiinteässä asennossa aluksen suhteen. Mutta he työntävät toisiaan, he alkavat erottua vastakkaisiin suuntiin, kun ne nähdään aluksesta.

Se voi palvella sinua: Big Bang -teoria: Ominaisuudet, vaiheet, todisteet, ongelmat

Tässä tapauksessa, koska astronautien välinen vuorovaikutus on vain heidän kätensä kosketusvoiman kautta, kokonainen lineaarinen hetki. Eli kokonaislineaarinen aika 0.

Kunkin astronautin lineaarinen hetki kuitenkin muuttui. Alun perin jokaisella oli lineaarinen hetki 0 aluksen suhteen, mutta työntämisen jälkeen yksi tulee ulos yhteen suuntaan ja toinen vastakkaiseen suuntaan, ei-nollat ​​lineaariset hetket, joilla.

Siten, kun yksittäiset hetket lisätään vektorisesti, alkuperäinen kokonaislineaarinen vauhti saadaan seurauksena, mikä on mitätön.

Toisaalta lineaarisen momentin säilyttäminen. Mutta seuraus sen massaa sen nopeudella on yhtä suuri kuin tuote, joka on saatu kertomalla toisen massa toisen nopeudella.

Esimerkki 2

Pentu on kelluvalla alustalla rauhallisten vesien järvellä ja sen omistaja näkee sen telakasta. Alussa sekä alusta että koiranpentu ovat levossa, mutta kun koiranpentu haluaa lähestyä omistajaa, alusta siirtyy pois telakasta.

Selitys tälle havainnolle on tarkalleen lineaarisen vauhdin säilyttämisen periaatteessa. Järjestelmä koostuu koiranpennusta ja alustasta.

Pentu voi kävellä laiturilla jalkojensa ja pinnan välisen kitkavoiman ansiosta, tässä tapauksessa kitkavoima on sisäinen vuorovaikutuksen voima sen ja alustan välillä.

Sarja on eristetty järjestelmä, ja alusta voi liikkua vaakasuoraan järvellä, vapaa kaikista liikkeenkestävyyksistä. Toisaalta pystysuunnassa kaikki voimat ovat tasapainossa ja kompensoituja, ja sarjassa ei ole liikettä siihen suuntaan.

Siksi tässä tilanteessa kaikki hypoteesit täyttyvät siten, että lineaarisen vauhdin säilyttämisperiaatetta sovelletaan.

Esimerkki 3

Eskimo on kiinni jäätelön keskellä, jää on niin sileä, että riippumatta siitä, kuinka paljon kokeiltu, eskimo liukuu ja pysyy aina samassa paikassa.

Ainoa mahdollinen tapa, jolla Eskimo poistuu järvestä, on, että se on suuntaan päinvastaisessa suunnassa, jota sen reppussa on raskas esine (olettaen, että yksi).

Voi palvella sinua: Geometrinen optiikka: Mitä tutkimuksia, lakeja, sovelluksia, harjoituksia

Sovellukset

Laittaa avaruuteen

Lineaarisen hetken säilyttäminen. Tässä tapauksessa aluksen impulssi saavutetaan karkottamalla kaasut suurella nopeudella, jotta raketti voi liikkua vastakkaiseen suuntaan, johon ne karkotettiin.

Jos alus on alun perin levossa, kun polttoaine poltetaan ja karkotetaan, karkotusvoima tapahtuu itse alusta vasten. Se on kaasujen ja laivan välinen sisäinen voima. Ulkovoimia ei ole, ja siksi se käyttää lineaarisen hetken säilyttämistä.

Koska kaasujen lineaarinen momentti on sama ja vastoin laivan, se onnistuu poistumaan ja jatkamalla kaasujen karkottamista, lisää sen liikkumista ja siksi sen nopeutta.

Jokapäiväinen elämä

Toinen tapaus lineaarisen hetken säilyttämiselle.

Voitaisiin väittää, että tässä tapauksessa periaatetta ei sovelleta, koska on olemassa ulkoinen voima: puun tarjoama vastus kynsille.

Kosketushetkellä voima, jonka vasara tulostaa kynsille.

Koko vasaran lineaarinen hetki, joka on melko suuri sen suuren massan ja nopeuden vuoksi, siirretään kynsiin heti törmäyksen jälkeen. Huomaa, että koko hetki siirretään, mutta ei kaikki vasaran kineettinen energia, koska osa siitä on muutettu lämpöenergiaksi kynsiksi ja vasaraksi, jotka nostavat sen lämpötilaa iskun jälkeen.

Harjoitukset

Harjoitus 1

Andrew ja Berenice -astronautit ovat avaruusasemalta, joka on otettu molemmista käsistä ja levossa aseman suhteen. He ajavat työntää kätensä toisiaan vastaan ​​ja heidät vapautetaan. Jos Andrew, 70 kg massa liikkuu nopeudella 1 m/s aseman suhteen, mikä on Berenicen nopeus 49 kg massaa?

Ratkaisu

Tässä tapauksessa lineaarisen vauhdin säilyttämisen hypoteesia sovelletaan selvästi, koska ulkoisessa tilassa ei ole ulkoisia voimia. Voima, jolla heidän kätensä työntävät molemmat astronautit, on sisäinen voima.

Se voi palvella sinua: aaltodiffraktio: käsite ja esimerkit

Oletetaan, että Andrew'n massa on m_-lla ja Berenice m_{b -}. Samoin molempien nopeudet impulssin jälkeen ovat V_-lla Andrewille ja V_{b -} Berenicelle. Sitten lineaarisen vauhdin säilyttämistä käytetään seuraavasti:

M_-lla∙0 - + M_{b -}∙0 - = M_-lla∙V_-lla+ M_{b -}∙V_{b -}

Berenicen nopeuden puhdistaminen:

V_{b -} = - (m_-lla / M_{b -}) ∙ V_-lla

Numeeristen arvojen sijoittaminen:

V_{b -} = - (70/49) ∙ (1m / s) tai = -1,43m/s tai

Toisin sanoen Berenice liikkuu nopeasti 1,43 m/s Andrewin vastakkaiseen suuntaan.

Harjoitus 2

Pentu kävelee kohti omistajansa puoliksi siirretyn alustan päälle. Lähde: f. Zapata.

5 kg -taikina on levossa 15 kg: n alustalla, joka kelluu, myös levossa, edelleen järvellä. Jos koiranpentu alkaa kävellä lavalla nopeudella 0,5 m/s tähän nähden. Kuinka nopeasti koiranpentu ja kiinteä tarkkailija?

Ratkaisu

Sitä pidetään inertiaalisena referenssijärjestelmänä laiturille, jossa pentunomistaja on. Aluksi sekä pentu että kelluva alusta ovat levossa telakan suhteen.

Kun koiranpentu päättää kävellä kohti omistajaa nopeasti V ' Alustan suhteen laituri siirtyy pois keväästä nopeudella +V. Pennun nopeus telakan suhteen saavutetaan sen nopeuden vektorisummalla alustan plus alustan nopeudella ja merkitsee sitä:

v = -v' + V

Koska veden vastus alustan liikkeeseen on käytännössä nolla sen alhaisesta nopeudesta, voidaan vahvistaa, että järjestelmä koostuu Pentu + alusta Se on eristetty järjestelmä ja lineaarisen vauhdin säilyttämisen periaatetta sovelletaan:

0 = M ∙ V + M ∙ V

Muistaa, että v = v ' + v sinulla on:

0 = -M ∙ V ' + M ∙ V + M ∙ V

Eli m ∙ v '= (m+m) ∙ v

Siksi v = [m/(m + m)] v 'y V = - (m/m) v = - [m/(m + m)] v'

Numeeristen arvojen korvaaminen on:

V = [5/(5 +15)] ∙ 0,5 m/s = 0,125 m/s

Tämä on nopeus, jolla jousalusta siirtyy.

V = -(15/20) ∙ 0,5 m/s = -0,375 m/s

Ja tämä on nopeus, jolla koiranpentu lähestyy telakkaa.

Viitteet

1. Duke University. Hiukkasten järjestelmät. Palautettu: WebHome.Pala.Herttua.Edu.
2. Rex, a. 2011. Fysiikan perusteet. Pearson.
3. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1. Pearson.
4. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Osa 1. Seitsemäs. Ed. Cengage -oppiminen.
5. Tipler, P. (2006). Fysiikka tieteen ja tekniikan puolesta. 5. ed. Osa 1. Toimitus palautti.