Boltzmannin vakiohistoria, yhtälöt, laskelmat, harjoitukset

Se Boltzmann Constant Se on termodynaamisen järjestelmän tai objektin keskimääräisen kineettisen energian arvoa, jonka absoluuttinen lämpötila on sama. Vaikka lämpötila ja energia eivät ole usein hämmentyneitä, ne eivät ole sama käsite.

Lämpötila on energian mitta, mutta ei itse energiaa. Boltzmann -vakiona yksi on linkitetty toisiinsa seuraavasti:

JA_c = (3/2) k_{B -}  T

Boltzmann -isäntä Wienissä. Lähde: dadotet englanniksi Wikipedia [CC BY-SA 3.0 (http: // creativecommons.Org/lisenssit/by-SA/3.0/]]

Tämä yhtälö pätee ihanteelliseen monoatoiseen kaasumolekyyliin m, missä JA_c Se on hänen kineettinen energia, joka on annettu Joulesissa, k_{B -} Se on Boltzmannin vakio ja T Se on absoluuttinen lämpötila Kelvinissä.

Tällä tavalla, kun lämpötila nousee, myös keskimääräinen kineettinen energia aineen molekyylin avulla kasvaa, kuten odotetaan tapahtuvan. Ja päinvastoin tapahtuu, kun lämpötila laskee, ja pystyy saavuttamaan pisteen, jossa koko liike loppuu, alhaisin mahdollinen tai absoluuttinen lämpötila saavutetaan.

Kun puhutaan keskimääräisestä kineettisestä energiasta. Ja hiukkaset voivat liikkua monin tavoin, esimerkiksi liikuttamalla, pyörivällä tai värähtelevällä. Tietysti kaikki eivät tee sitä samalla tavalla, ja koska ne ovat lukemattomia, niin keskiarvo on karakterisoimalla järjestelmä.

Jotkut energiatilat ovat todennäköisemmin kuin toiset. Tällä käsitteellä on radikaali merkitys termodynamiikassa. Edellisessä yhtälössä tarkasteltu energia on translaation kineettinen energia. Valtioiden todennäköisyydestä ja niiden suhde Boltzmann -vakioon puhuvat vähän myöhemmin.

Vuonna 2018 Kelvin määritettiin uudelleen ja hänen kanssaan Boltzmann -vakio, joka kansainvälisessä järjestelmässä on noin 1.380649 x 10^-23 J -. K -k -^-1. Boltzmann -vakiolle voidaan saavuttaa paljon tarkempi tarkkuus, joka on määritetty lukuisissa laboratorioissa ympäri maailmaa, eri menetelmillä.

[TOC]

Historia

Kuuluisa vakio velkaa nimensä Wienissä syntynyt fyysikko Ludwig Boltzmannille (1844-1906), joka omistautui tiedemiehenä tutkimaan järjestelmien tilastollista käyttäytymistä monien hiukkasten kanssa Newtonin mekaniikan kannalta.

Vaikka nykyään atomin olemassaolo hyväksytään yleisesti, 1800 -luvulla uskomus siitä, oliko atomi todella olemassa vai onko se keino, jolla selitettiin monia fyysisiä ilmiöitä, oli täydessä keskustelussa täydessä keskustelussa.

Voi palvella sinua: Normaali vektori: Laskenta ja esimerkki

Boltzmann oli vahva puolustaja atomin olemassaololle, ja hänen aikansa aikana hän kohtasi monien kollegoidensa ankaraa kritiikkiä, jotka katsoivat, että ne sisälsivät liukenemattomia paradokseja.

Hän ilmoitti, että havaittavat ilmiöt makroskooppisilla tasoilla voitaisiin selittää aineosien hiukkasten, kuten atomien ja molekyylien, tilastollisilla ominaisuuksilla.

Tämä kritiikki voi johtua syvästä masennusjaksosta, joka sai hänet ottamaan oman elämänsä syyskuun 1906 alussa, kun hänellä oli vielä paljon tekemistä, koska häntä pidettiin yhtenä aikansa suurista teoreettisista fyysikoista ja siellä siellä ja siellä oli vähän siihen, että muut tutkijat auttavat vahvistamaan teoriansa todenmukaisuutta.

Se ei tapahtunut kauan hänen kuolemansa jälkeen, kun uusia löytöjä atomin luonteesta ja hänen perustajansa hiukkasista lisätään syylle Boltzmannille.

Boltzmannin vakio ja Planckin teokset

Nyt Boltzmannin vakio k -k -_{B -} Se esiteltiin sellaisena kuin se tunnetaan tänään jonkin aikaa Itävallan fyysikon työn jälkeen. Se oli Max Planck, hänen vuonna 1901 esittämänsä työn päästöinsä, joka tuolloin antoi hänelle arvon 1,34 x 10²³ J/k.

Vuoteen 1933 mennessä Boltzmann lisättiin Wieniin julisteiden kunnianosoituksena Plaque -määritelmällä entropia, johon kuuluisa vakio: S = k_{B -} loki w, yhtälö, josta keskustellaan myöhemmin.

Nykyään Boltzmannin vakio on välttämätöntä termodynaamisten lakien, tilastollisen mekaniikan ja informaatioteorian soveltamisessa, joista tämä fyysikko, jolla oli surullinen pää, oli edelläkävijä.

Arvo ja yhtälöt

Kaasuja voidaan kuvata makroskooppisesti ja myös mikroskooppisesti. Ensimmäisessä kuvauksessa on käsitteitä, kuten tiheys, lämpötila ja paine.

On kuitenkin muistettava, että kaasu koostuu monista hiukkasista, joilla on globaali taipumus tiettyyn käyttäytymiseen. Se trendi mitataan makroskooppisesti. Yksi tapa määrittää Boltzmannin vakio on ihanteellisten kaasujen tunnetun yhtälön ansiosta:

p.V = n. R -. T

Tässä p Se on kaasun paine, V Se on sen tilavuus, n Se on läsnä olevien moolien lukumäärä, R - Se on kaasujen vakio ja T Se on lämpötila. Ihanteellisen kaasun moolissa seuraava tuotteen välinen suhde täyttyy p.V, ja käännöksen kineettinen energia K -k - Koko sarja on:

Voi palvella sinua: Corpuscular -malli aineesta

p.V = (2/3). K -k -

Siksi kineettinen energia on:

K = (3/2) n.R -.T

Jakamalla läsnä olevien molekyylien kokonaismäärä, jota kutsutaan n, saadaan yhden hiukkasen keskimääräinen kineettinen energia:

JA_c = K /n

JA_c= (3/2n) n.R -.T

Molissa on hiukkasten lukumäärä n_-Lla, Ja siksi hiukkasten kokonaismäärä on N = nnA, pysyminen:

JA_c = (3/2nn_-Lla) n.R -.T

Tarkalleen osamäärä R/n_-Lla Boltzmannin vakiona on osoitettu, että hiukkasen keskimääräisen translaation kineettinen energia riippuu vain absoluuttisesta lämpötilasta eikä muista suuruuksista, kuten paineesta, tilavuudesta tai jopa molekyylin tyypistä:

JA_c = (3/2) k_{B -.} T

Boltzmannin vakio ja entropia

Kaasulla on tietty lämpötila, mutta tämä lämpötila voi vastata erilaisia ​​sisäisiä energiatiloja. Kuinka visualisoida tämä ero?

Harkitse 4 kolikon samanaikaista käynnistämistä ja tapoja, joilla ne voivat pudota:

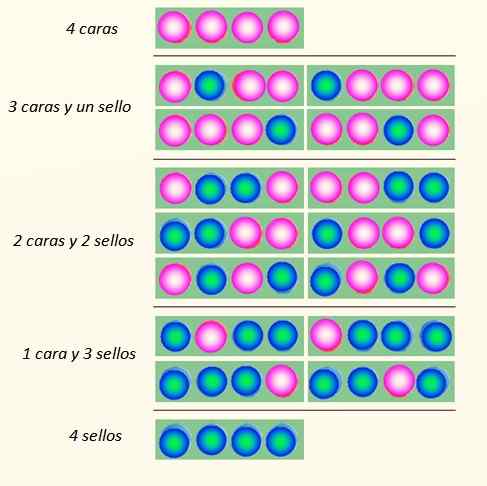Tapoja, joilla 4 kolikkoa voi pudota. Lähde: Itse tehty

Kolikkosarja voi olettaa yhteensä 5 osavaltiota, joita harkitaan Makroskooppinen, kuvassa kuvattu. Mitkä näistä valtioista lukija sanoisi, että se on todennäköisin?

Vastauksen tulisi olla 2 kasvot ja 2 ristiä, koska siinä on yhteensä 6 mahdollisuutta, 16: sta kuvasta kuvattua. Ja 2⁴ = 16. Nämä vastaavat valtioita mikroskooppinen.

Ja entä jos 20 kolikkoa käynnistetään 4: n sijasta? Siellä olisi yhteensä 2^{kaksikymmentä} mahdollisuudet tai "mikroskooppiset tilat". Se on paljon suurempi ja vaikeampi määrä käsitellä. Suurten määrien hallinnan helpottamiseksi logaritmit ovat erittäin tarkoituksenmukaisia.

Nyt näyttää siltä, ​​että valtio, jolla on suurin häiriö, on todennäköisin. Tilatut valtiot, kuten 4 kasvot tai 4 leimaa, ovat hiukan vähemmän todennäköisiä.

Makroskooppisen tilan entropia määritellään seuraavasti:

S = k_{B -} ln w

Missä W - Se on mahdollisten mikroskooppisten tilojen lukumäärä ja k -k -_{B -} Se on Boltzmannin vakio. Kuten ln w Se on ulottumaton, entropialla on samat yksiköt kuin k_{B -}: Joule/k.

Tämä on kuuluisa yhtälö Boltzmannin hautakivessä Wienissä. Kuitenkin enemmän kuin entropia, asiaankuuluva on sen muutos:

Se voi palvella sinua: termodynaamiset muuttujat: mitkä ovat ja harjoitukset ratkaistaan

ΔS = k_{B -} ln w₂ - k -k -_{B -} ln w₁ = k_{B -} ln (w₂/w₁-A

Kuinka k lasketaan_{B -}?

Boltzmann -vakion arvo saadaan kokeellisesti tarkasti mittauksiin, jotka perustuvat akustinen lämpömometria, jotka suoritetaan käyttämällä ominaisuutta, joka luo riippuvuuden äänen nopeudesta kaasussa, jonka lämpötila on sama.

Todellakin, äänen nopeus kaasussa antaa:

Missä b _{adiabaattinen} Se on adiabaattinen puristusmoduuli, jonka on antanut:

B -_{adiabaattinen} = γp

Ja ρ on kaasutiheys. Edelliselle yhtälölle, p Se on kyseisen kaasun paine ja γ Se on adiabaattinen kerroin, jonka arvo tietylle kaasulle löytyy taulukoista.

Metrologian instituutiot kokevat myös muita tapoja mitata vakiona, kuten Johnson -kohinan lämpömetria, joka käyttää lämmönvaihtelua, joita tapahtuu satunnaisesti materiaaleissa, erityisesti ohjaimissa.

Ratkaisut

-Harjoitus 1

Löytö:

a) keskimääräisen käännöksen kineettinen energia JA_c jolla on ihanteellinen kaasumolekyyli 25 ºC: n lämpötilassa

b) käännöksen kineettinen energia K -k - tämän kaasun 1 moolista molekyyleistä

c) Happimolekyylin keskimääräinen nopeus 25 ° C: ssa

Tosiasia

m_happi = 16 x 10 ^-3 kg/mol

Ratkaisu

to) JA_c = (3/2) k t = 1.5 x 1.380649 x 10^-23J -. K -k -^-1 x 298 K = 6.2 x 10^{-kaksikymmentäyksi} J -

b) K = (3/2) n.R -.T = 5 x 1 mol x 8.314 j/mol .K X 298 K = 3716 J

c) JA_c = ½ MV², Kun otetaan huomioon, että happimolekyyli on diatominen ja molaarimassa on kerrottava 2: lla, se on:

-Harjoitus 2

Löydä entropian muutos, kun 1 mol kaasua, jonka tilavuus on 0.5m³ Se laajenee miehittämään 1 m³.

Ratkaisu

ΔS = k_{B -} ln (w₂/w₁-A

W -₂= 2^NW -₁ (Niitä oli 2⁴ Mikroskooppiset tilat 4 kolikon käynnistämiseksi, muista?-A

Missä n on hiukkasten lukumäärä, joka on läsnä 0.5 mol kaasua 0.5 x n_-Lla-

ΔS = k_{B -} ln (2^N W -₁/w₁) = k_{B -} 2^N= k_{B -} 0 -.5N_-Lla ln 2 = 2.88 J/K

Viitteet

1. Atkins, p. 1999. Fysikaalinen kemia. Omega -versiot. 13-47.
2. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill. 664-672.
3. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. 6. ... Ed Prentice Hall. 443 -444.
4. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1. 647-673.
5. Jos uudelleenmääritys. Kelvin: Boltzmann Constant. Toipunut: NIST.Hallitus