Mikä on tilastollinen alue? (Esimerkkejä)

Hän etäisyys, Kiertue tai amplitudi, tilastoissa, on ero (vähennys) maksimiarvon ja näytteen tai populaation tietojoukon minimiarvon välillä. Jos R -kirjaimen ja datan kanssa x, Alueen kaava on yksinkertaisesti:

R = x_max - x_mini

 Missä x_max Se on datan enimmäisarvo ja x_mini Se on minimi.

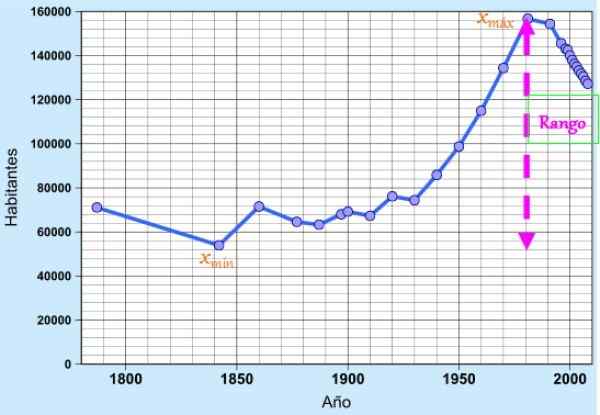
Kuvio 1. Cádizin väestöä vastaava tietoalue viimeisen kahden vuosisadan aikana. Lähde: Wikimedia Commons.

Konsepti on erittäin hyödyllinen yksinkertaisena dispersiomittauksena tietojen vaihtelun nopeasti arvostamiseksi, koska se osoittaa sen ajan jatkamisen tai pituuden, missä nämä löytyvät.

Oletetaan esimerkiksi, että yliopiston ensimmäisen tekniikan vuoden miesopiskelijan ryhmän ryhmä. Ryhmän korkein opiskelija mittaa 1.93 m ja alin 1.67 m. Nämä ovat näytetietojen ääriarvoja, joten niiden reitti on:

R = 1.93 - 1.67 m = 0.26 m tai 26 cm.

Tämän ryhmän opiskelijoiden kohta on jaettu koko alueelle.

[TOC]

Hyödyt ja haitat

Alue on, kuten aiemmin totesimme, mitta siitä, kuinka dispergoituja tietoja on. Pieni alue osoittaa, että tiedot ovat enemmän tai vähemmän lähellä ja dispersio on vähän. Toisaalta suurempi alue osoittaa, että tiedot ovat dispergoituneempia.

Alueen laskemisen edut ovat ilmeisiä: se on hyvin yksinkertainen ja nopea löytää, koska se on yksinkertainen ero.

Sillä on myös samat yksiköt kuin se, jolla se toimii, ja konsepti on erittäin helppo tulkita kaikille tarkkailijoille.

Esimerkissä tekniikan opiskelijoiden asemasta, jos alue olisi ollut 5 cm, sanoisimme, että opiskelijat ovat kaikki samankokoisia. Mutta etäisyydellä 26 cm oletamme heti, että näytteessä on kaikkien välitasojen opiskelijoita. Onko tämä oletus aina oikein?

Se voi palvella sinua: Ero ympyrän ja kehän välillä (esimerkkien kanssa)

Alueen haitat dispersiomittarina

Jos katsomme huolellisesti, 25 tekniikan opiskelijan otoksessamme, vain yksi heistä mittaa 1.93 ja jäljellä olevilla 24: llä on arkistot lähellä 1.67 m.

Ja silti alue pysyy samana, vaikkakin on täysin mahdollista, että päinvastoin: että enemmistön asema heilahtelee noin 1.90 m ja vain yksi mittaa 1.67 m.

Joka tapauksessa tietojen jakautuminen on hyvin erilaista.

Alueen haitat dispersiomittarina johtuvat siitä, että se käyttää vain ääriarvoja ja jättää huomiotta kaikki muut. Koska suurin osa tiedoista menetetään, ei ole aavistustakaan, kuinka näytetiedot jakautuvat.

Toinen tärkeä ominaisuus on, että näytteen alue ei koskaan vähene. Jos lisäämme lisätietoja, ts. Tarkastelemme lisää tietoa, alue kasvaa tai pysyy samana.

Ja joka tapauksessa se on hyödyllinen vain pienten näytteiden kanssa työskennellessäsi, sen ainutlaatuista käyttöä ei suositella dispersion mittana suurissa näytteissä.

On tehtävä täydentää muiden dispersiotoimenpiteiden laskemista, joissa otetaan huomioon kokonaistietojen toimittamat tiedot: reitti Kvartilinen, varianssi, keskihajonta ja variaatiokerroin.

Kondriilien välinen reitti, kvartiilit ja ratkaistu esimerkki

Olemme ymmärtäneet, että alueen heikkous dispersiomittana on, että se käyttää vain datan jakautumisen ääriarvoja, jättäen muut pois.

Välttää tämä haitta, kvartiilit: kolme arvoa, joka tunnetaan nimellä sijaintitoimenpiteet.

He jakavat tiedot, joita ei ole ryhmitelty neljään osaan (muut laajalti käytetyt sijaintitoimenpiteet ovat Desilit ja prosentti-A. Nämä ovat sen ominaisuuksia:

-Ensimmäinen kvartiili Q₁ Tietojen arvo on siten, että 25 % niistä on vähemmän kuin Q₁.

Voi palvella sinua: Suhteellisuusvakio: Mikä on, laskenta, harjoitukset

-Toinen kvartiili Q₂ Se on mediaani jakautumisesta, mikä tarkoittaa, että puolet (50 %) tiedoista on pienempi kuin tämä arvo.

-Lopuksi kolmas kvartiili Q₃ huomauttaa, että 75 % tiedoista on vähemmän kuin Q₃.

Sitten neliömäinen alue tai kvartiilien välinen reitti määritellään erona kolmannen kvartiilin Q: n välillä₃ ja ensimmäinen kvartiili Q₁ Tietojen perusteella:

Välimaailman interquotile -matka = R_{Q -} = Q₃ - Q -₁

Tällä tavalla arvon arvo R -arvo_{Q -} Extreme -arvot eivät vaikuta siihen niin. Siksi on suositeltavaa käyttää sitä puolueellisten jakautumisten, kuten erittäin korkean tai erittäin alhaisen opiskelijan, kun kyse on edellä kuvattu.

- Cuartyles -laskelma

Niiden laskemiseen on useita tapoja, tässä ehdotamme sellaista, mutta joka tapauksessa on tarpeen tuntea tilauksen määrä "N_jompikumpi”, Joka on paikka, joka viettää kvartiilin jakeluun.

Eli jos esimerkiksi q vastaa termiä₁ on toinen, kolmas tai neljäs ja niin jakauma.

Ensimmäinen kvartiili

N_jompikumpi (Q₁) = (N+1) / 4

Toinen kvartiili tai mediaani

N_jompikumpi (Q₂) = (N+1) / 2

Kolmas kvartiili

N_jompikumpi (Q₃) = 3 (n+1) / 4

Missä n on datanumero.

Mediaani on arvo, joka on oikeassa jakelun keskellä. Jos tiedonumero on pariton, sen löytämisessä ei ole mitään ongelmaa, mutta jos se on tasaista, niin kaksi keskusarvoa on keskiarvo, jotta ne muuttuvat yhdeksi.

Kun tilausnumero on laskettu, noudatetaan yhtä näistä kolmesta säännöstä:

-Jos sinulla ei ole desimaaleja, jakeluun ilmoitetut tiedot haetaan ja tämä on neljäs haku.

-Kun tilausnumero on puolivälissä kahden välillä, silloin koko osa osoittaa seuraavan tosiasian keskiarvoa, ja tulos on vastaava kvartiili.

-Jokaisessa muussa tapauksessa lähin kokonaisluku on pyöristetty ja se on neljäs paikka.

Voi palvella sinua: Lisäaineperiaate

Ratkaistu esimerkki

Asteikolla 0 - 20, 16 matematiikan opiskelijan ryhmä sain seuraavat arvosanat (pisteet) osittaisessa kokeessa:

16, 10, 12, 8, 9, 15, 18, 20, 9, 11, 1, 13, 17, 9, 10, 14

Löytö:

a) Tiedot tai tietoreitti.

b) kvartiilien arvot q₁ ja Q₃

c) kvartilojen välinen alue.

Kuva 2. Suorita tämän matematiikkakokeen pätevyys niin paljon vaihtelua? Lähde: Pixabay.

Liittää jhk

Ensimmäinen asia reitin löytämiseksi on tilata tiedot kasvavat tai vähenevät. Esimerkiksi kasvavassa järjestyksessä sinulla on:

1, 8, 9, 9, 9, 10, 10, 11, 12, 13, 14, 15, 16, 17, 18, 20

Alussa annetun kaavan kautta: r = x_max - x_mini

R = 20 - 1 pistettä = 19 pistettä.

Tuloksen mukaan näillä arvosanoilla on suuri hajonta.

Ratkaisu b

N = 16

N_jompikumpi (Q₁) = (N + 1) / 4 = (16 + 1) / 4 = 17/4 = 4.25

Se on desimaalien lukumäärä, jonka koko osa on 4. Sitten siirrymme jakeluun, neljännen sijan käyttäviä tietoja etsitään ja sen arvo on keskiarvo viidennen aseman arvon kanssa. Koska molemmat ovat 9, keskiarvo on myös 9 ja sitten: sitten:

Q -₁ = 9

Nyt toistamme menettelyn löytää q₃-

N_jompikumpi (Q₃) = 3 (n +1) / 4 = 3 (16 +1) / 4 = 12.75

Jälleen se on desimaali, mutta koska se ei ole puolivälissä, se on pyöristetty 13: een. Haettu kvartiili vie kolmetoista sijaintia ja on:

Q -₃ = 16

Liuos C

R -_{Q -} = Q₃ - Q -₁ = 16 - 9 = 7 pistettä.

Se, kuten näemme.

Viitteet

1. Berenson, m. 1985. Hallinnon ja taloustieteen tilastot. Inter -American S.-Lla.
2. Canavos, G. 1988. Todennäköisyys ja tilastot: Sovellukset ja menetelmät. McGraw Hill.
3. DeVore, J. 2012. Tekniikan ja tieteen todennäköisyys ja tilastot. Kahdeksas. Painos. Kyynärmä.
4. Esimerkkejä kvarteista. Haettu osoitteesta: matematiikka10.netto.
5. Levin, r. 1988. Järjestelmänvalvojien tilastot. Toinen. Painos. Prentice Hall.
6. Walpole, r. 2007. Tekniikan ja tieteen todennäköisyys ja tilastot. Pearson.