Implisiittiset johdannaiset, kuinka ne on ratkaistu ja ratkaistuihin harjoituksiin

Se implisiittiset johdannaiset Ne ovat työkaluja, joita käytetään toimintoihin sovelletussa erottelutekniikassa. Niitä sovelletaan, kun se ei ole mahdollista säännöllisissä menetelmissä, suorita riippuvaisen muuttujan puhdistuma. Tämä puhdistuma tehdään riippumattoman muuttujan perusteella.

Esimerkiksi lausekkeessa 3xy³ - 2y + xy² = XY, et voi saada lauseketta, joka määrittelee "y" riippuen "x". Niin, että kun differentiaalinen ekspressio, dy/dx voidaan saada.

[TOC]

Kuinka implisiittiset johdannaiset on ratkaistu?

Vaikutuksen ratkaisemiseksi se perustuu implisiittiseen ilmaisuun. Esimerkiksi: 3xy³ - 2y + xy² - Xy = 0. Tämä on jo selkeästi puhdistettu, mutta sen tekeminen ei ole välttämätön ehto Y: n johdannaisen saamiseksi X: n suhteen. Sitten jokainen elementti on johdettu kunnioittamaan sekoitetun toiminnon ketjusääntöä:

3xy³ Se koostuu kahdesta muuttujasta, siksi D (3xy³) Sitä käsitellään toimintojen tuotteen johdannaisena.

D (3xy³)/dx = 3y³ + 3y².(3x) ja '= 3y³ + 9xy² ja'

Missä elementti ja 'tunnetaan nimellä "ja serkku”Ja dy/dx edustaa

-2y saadaan lain mukaan.U = k.TAI'

D (-2y) = -2 ja '

Xy² Oletetaan, että toinen toimintojen tuote koostuu erilaisesta erotuksesta

D (xy²) = y² + 2xy ja '

-XY on homologinen tapa

d (-xy) = -y -x ja '

Ne korvataan tasa -arvoisesti tietäen, että nolla johdannainen on nolla.

3y³ + 9xy² ja ' - 2 ja' + ja² + 2xy ja ' - y - x ja' = 0

Elementit, joilla on termi ja 'on ryhmitelty tasa -arvon toiselle puolelle

Voi palvella sinua: kolineaalivektorit

3y³ + ja² - y = -9xy² ja ' + 2 ja' + x ja '

Yleinen tekijä ja 'tasa -arvon oikeassa jäsenessä poistetaan

3y³ + ja² - y = y '(-9xy² + x + 2)

Lopuksi termi, joka moninkertaistaa ja '. Siten saamassa ekspressio, joka vastaa y: n implisiittistä johdannaista x: stä.

ja '= dy/dx = (3y³ + ja² - y)/(-9xy² + x + 2)

Ketjusääntö

Implisiittisessä johdannaisessa ketjusääntöä kunnioitetaan aina. Kaikki differentiaaliset lausekkeet annetaan riippumattomasta muuttujasta x. Niin, että minkä tahansa X: n erilaisen muuttujan on sisällettävä termi dθ/dx johdetun jälkeen.

Tämä termi ilmestyy vain ensimmäisen asteen tai eksponentin kanssa yhtä kuin 1. Tämä laatu tekee siitä täysin selvän perinteisillä tekijämenetelmillä. Niin, että on mahdollista saada lauseke, joka määrittelee differentiaalisen dθ/dx.

Ketjusäännössä esitetään erilaistumisen tai johdannaisprosessin asteittainen luonne. Jos minkä tahansa komposiittifunktion f [g (x)]: n f -differentiaalisen ekspression on oltava

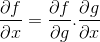
Toimintatilaus

Jokaisessa sovellettavassa kaava- tai johdannaislaissa muuttujien järjestys on otettava huomioon. Riippumattomaan muuttujaan liittyvät kriteerit kunnioitetaan muuttamatta sen korrelaatiota riippuvaisen muuttujan kanssa.

Riippuvaisen muuttujan suhde johdetun ajankohtana otetaan suoraan.; Lukuun ottamatta sitä, että tätä pidetään toisena funktiona, minkä vuoksi sekoitettujen funktioiden ketjusääntökriteerit sovelletaan.

Tätä voidaan kehittää lausekkeissa, joissa on yli 2 muuttujaa. Samoin periaatteiden mukaan kaikki riippuvaisiin muuttujiin viittaavat erot merkitään.

Voi palvella sinua: mikä on ohje? (Geometria)

Graafisesti käsitellään samoja kriteerejä, jotka määrittelevät johdannaisen. Vaikka johdannainen on tason käyrän tangentin viivan kaltevuus, loput riippuvaisiin muuttujiin kuuluviin eroihin (DY/DX, DZ/DX) edustavat tangenttitasoja vektorirunkoihin.

Implisiittinen funktio

Sanotaan².

3xy³ - 2y + xy² = x ja voidaan kirjoittaa 3xy -muodossa³ - 2y + xy² - Xy = 0

Kun otetaan huomioon funktion y = f (x) selittämisen mahdottomuus selittää.

Historia

Eri matemaattiset tutkijat alkoivat nimittää differentiaalilaskennan noin 1700 -luvulla. Ensimmäinen kerta, kun se mainittiin, oli Newtonin ja Leibnizin panoksen kautta. Molemmat käsittelivät differentiaalilaskentaa eri näkökulmista, mutta lähentyivät tuloksia.

Vaikka Newton keskittyi erilaistumiseen nopeuden tai variaationopeudeksi, Leibniz -lähestymistapa oli geometrisempi. Voidaan sanoa, että Newton hyökkäsi Apollonius of Perge- ja Leibnizin jättämiin oletuksiin Ferman geometriset ideat.

Implisiittinen johdanna. He laajensivat Leibnizin geometrisen käsitteen r³ ja jopa moniulotteiset tilat.

Sovellukset

Erilaisissa tilanteissa käytetään implisiittisiä johdannaisia. Ne ovat yleisiä valuuttakurssi -ongelmissa liittyvien muuttujien välillä, joissa muuttujia pidetään tutkimuksen tunteesta riippuen riippuvaisia ​​tai riippumattomia.

Heillä on myös mielenkiintoisia geometrisia sovelluksia, kuten heijastus- tai varjoongelmissa, kuvioissa, joiden muoto voidaan mallintaa matemaattisesti.

Voi palvella sinua: kiintiön näytteenotto: menetelmä, edut, haitat, esimerkit

Niitä käytetään usein talouden ja tekniikan aloilla sekä luonnonilmiöiden ja kokeellisten rakennusten erilaisissa tutkimuksissa.

Ratkaisut

Harjoitus 1

Määritä implisiittinen lauseke, joka määrittelee DY/DX

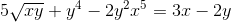
Jokainen elementti on erilainen kuin lauseke

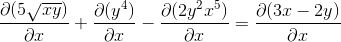
Ketjusäännön määrittäminen kussakin pätevässä tapauksessa

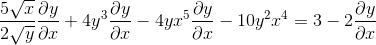
Ryhmittely tasa -arvon toiselle puolelle elementit, joilla on DY/DX

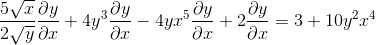
Factoring käyttämällä yhteistä tekijää

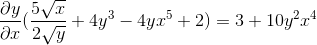
Puhdistetaan hankkimalla kysytty lauseke

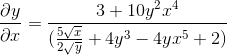
Harjoitus 2

Määritä implisiittinen lauseke, joka määrittelee DY/DX

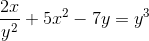
Ilmaisee johdannaisia ​​toteutettavissa

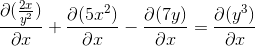
Implisiittisesti johdetaan ketjusäännön mukaan

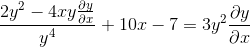
Factoring yhteiset elementit

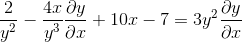
Termin Dy/DX: n ryhmitteleminen tasa -arvon toiselle puolelle

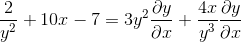
Yleinen tekijä differentiaalielementille

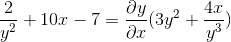
Tyhjentämme ja saamme halutun ilmaisun

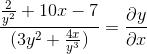
Viitteet

1. Yhden muuttujan laskenta. Ron Larson, Bruce H. Edwards. Cengage Learning, 10. marraskuuta. 2008
2. Implisiittinen funktion lause: historia, teoria ja sovellukset. Steven G. Krantz, Harold R. Puistot. Springer Science & Business Media, 9. marraskuuta. 2012
3. Monimuuttuja -analyysi. Sable Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13. joulukuuta. 2010
4. Järjestelmän dynamiikka: Mechatronic -järjestelmien mallintaminen, simulointi ja hallinta. Dekaani C. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7. maaliskuuta. 2012
5. Laskenta: Matematiikka ja mallinnus. William Bauldry, Joseph R. Fiedler, Frank R.Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1. tammikuuta. 1999