Osittaiset johdannaiset ominaisuudet, laskelmat, harjoitukset

Se osittaiset johdannaiset Useiden riippumattomien muuttujien funktiosta ovat ne, jotka saavutetaan ottamalla tavallinen johdannainen johonkin muuttujasta, kun taas muita ylläpidetään tai otetaan vakiona.

Yhden muuttujan osittainen johdannainen määrittää, kuinka funktio vaihtelee kussakin pisteessä, muutosyksikköä kohti. 

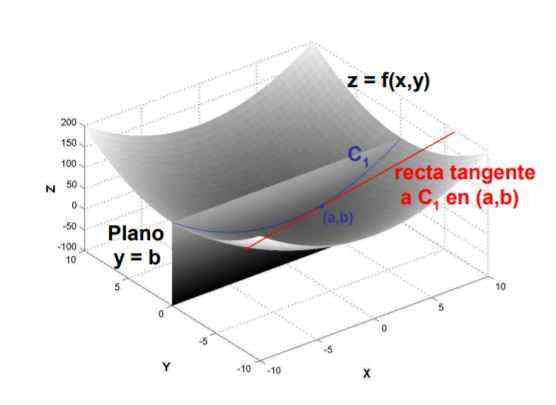Kuvio 1. Tangenttiviivan kaltevuus käyrään, joka muodostuu tason y = b leikkauspinnan kanssa pinnan f (x, y) pisteessä (a, b) on f: n osittainen johdannainen suhteessa X: ään, arvioitu siinä vaiheessa. Lähde: UPM.On

Määritelmänsä vuoksi osittainen johdannainen lasketaan ottaen osamäärän matemaattisen rajan funktion variaation ja muuttujan variaation välillä siitä, mikä on johdettu, kun jälkimmäisen muutoksella on taipumus nolla.

Oletetaan, että funktion tapaus F Se riippuu muuttujista x ja ja, toisin sanoen jokaiselle parille (X, y) A on osoitettu z -z- 

f: (x, y) → z .

Funktion osittainen johdannainen z = f (x, y), kuin x on määritelty seuraavasti:

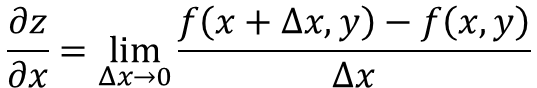
Nyt on olemassa useita tapoja merkitä funktion osittaista johdannaista, esimerkiksi:

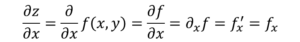
Ero tavallisen johdannaisen kanssa merkinnän kannalta on d -d johdannainen muutetaan symboliksi ∂, tunnetaan nimellä "Jacobi D".

[TOC]

Osittaisten johdannaisten ominaisuudet

Useiden muuttujien funktion osittainen johdannainen yhdestä niistä on tavanomainen johdannainen mainitussa muuttujassa ja ottaen loput kiinteänä tai vakiona. Osittaisen johdannaisen löytämiseksi tavallisten johdannaisten johdannaisääntöjä voidaan käyttää.

Pääominaisuuksien alapuolella:

Voi palvella sinua: Yleinen tekijä ryhmittelyssä: Esimerkkejä, harjoituksia

Jatkuvuus

Jos toiminto f (x, y) on osittaisia ​​johdannaisia x ja ja asiaan (Xo, minä) Sitten voidaan sanoa, että funktio on jatkuvaa siinä vaiheessa.

Ketjusääntö

Toiminto f (x, y) Jatkuvilla osittaisilla johdannaisilla x ja ja, joka puolestaan ​​riippuu parametrista t kautta x = x (t) ja y = y (t), Sillä on tavallinen johdannainen muuttujan suhteen t, joka lasketaan ketjusääntöllä:

d -d_t Z = ∂_xz d_tx + ∂_jaz d_tja

Sulkeminen tai lukitusominaisuus

Osittainen johdannainen suhteessa yhden funktion muuttujiin F kahdesta tai useammasta muuttujasta (X, y, ...), Se on toinen toiminto g Esimerkiksi samoissa muuttujissa: 

G (x, y, ...) = ∂_ja f (x, y, ...)

Toisin sanoen osittainen johdannainen on operaatio, joka menee R: stäⁿ a rⁿ. Tässä mielessä sanotaan, että se on a suljettu toiminta.

Peräkkäiset osittaiset johdannaiset

Useiden muuttujien funktion peräkkäiset osittaiset johdannaiset voidaan määritellä, mikä johtaa uusiin toimintoihin samoissa riippumattomissa muuttujissa.

Olla toiminto f (x, y). Seuraavat peräkkäiset johdannaiset voidaan määritellä:

F_Xx = ∂_xF ;  F_Yy = ∂_YyF ; F_Xy = ∂_XyF ja F_Yx = ∂_YxF

Kaksi viimeistä tunnetaan nimellä Sekajohdannaiset Koska niihin liittyy kaksi erilaista riippumatonta muuttujaa.

Schwarz -lause

Olla toiminto f (x, y), määritelty siten, että sen osittaiset johdannaiset ovat jatkuvia funktioita avoimessa alaryhmässä R -².

Joten jokaiselle parille (X, y) Se, että he kuuluvat mainitulle osajoukkoille, sekalaiset johdannaiset ovat identtisiä:

∂_XyF = ∂_YxF

Aikaisempi lausunto tunnetaan nimellä Schwarz -lause.

Kuinka osittaiset johdannaiset lasketaan?

Osittaiset johdannaiset lasketaan samanlaisia ​​kuin tavalliset funktiot johdannaiset yhdessä riippumattomassa muuttujassa. Kun useiden muuttujien funktion osittainen johdannainen otetaan yhdestä niistä, muut muuttujat otetaan vakiona.

Voi palvella sinua: puolet 15: stä

Alla on useita esimerkkejä:

Esimerkki 1

Ole funktio:

f (x, y) = -3x² + 2 (ja - 3)²

Ensimmäinen osittainen johdannainen pyydetään laskemaan x ja ensimmäinen osittainen johdannainen suhteessa ja.

Menettely

Osittaisen laskemiseksi F kuin x, On otettu ja vakiona:

∂_xF = ∂_x(-3x² + 2 (ja - 3)² ) = ∂_x(-3x² )+ ∂_x(2 (ja - 3)² ) = -3 ∂_x(x²) + 0 = -6x.

Ja puolestaan ​​laskea johdannainen ja On otettu x vakiona:

∂_jaF = ∂_ja(-3x² + 2 (ja - 3)² ) = ∂_ja(-3x² )+ ∂_ja(2 (ja - 3)² ) = 0 + 2 · 2 (y - 3) = 4y - 12.

Esimerkki 2

Määritä toisen asteen osittaiset johdannaiset:  ∂_Xxf, ∂_Yyf, ∂_YxF ja ∂_XyF Samaan toimintoon F esimerkin 1.

Menettely

Tässä tapauksessa, koska ensimmäinen osittainen johdannainen on jo laskettu x ja ja (Katso esimerkki 1):

∂_XxF = ∂_x(∂_xf) = ∂_x(-6x) = -6

∂_YyF = ∂_ja(∂_jaf) = ∂_ja(4y - 12) = 4

∂_YxF = ∂_ja(∂_xf) = ∂_ja(-6x) = 0

∂_XyF = ∂_x(∂_jaf) = ∂_x(4y - 12) = 0

On havaittu, että ∂_YxF = ∂_XyF, Täten Schwarzin lauseen täyttäminen, funktion jälkeen F ja sen ensimmäisen tilauksen osittaiset johdannaiset ovat kaikki jatkuvia toimintoja R -².

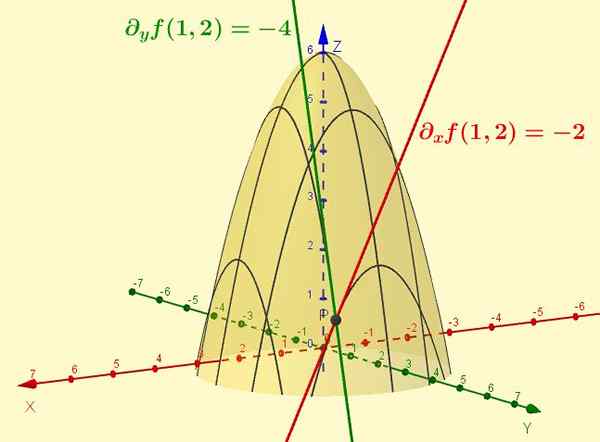
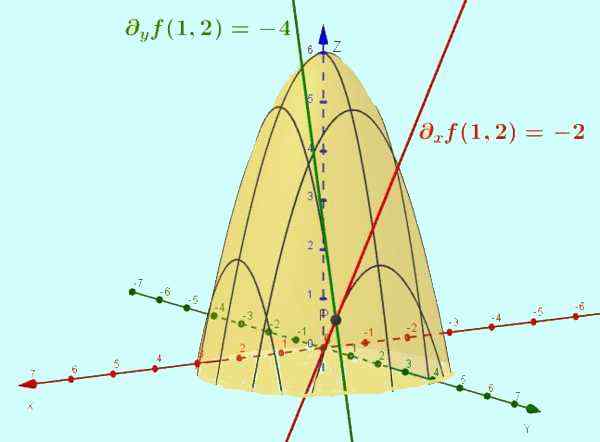Kuva 2. Funktio z = f (x, y) = -x2 - y2 + 6 on kuvassa esitetty pinta. Osittainen johdannainen X: n suhteen on käyrän tangenttiviivan kaltevuus, joka johtuu mainitun pinnan leikkauksesta tason Y = CTTE: n kanssa (erityistapaus on osoitettu y = 2). Samoin F: n osa suhteessa ja on tangentin kaltevuus risteykseen x = 1: n kanssa, pisteessä (1, 2, 1).

Ratkaisut

Harjoitus 1

Ole funktio:

Voi palvella sinua: neliömäiset peräkkäit: Esimerkkejä, sääntöä ja harjoituksia ratkaistu

f (x, y) = -x² - ja² + 6

Etsi toiminnot G (x, y) = ∂_xF  ja H (x, y) = ∂_jaF.

Ratkaisu

Osittainen johdannainen F kuin x, joille muuttuja ja Siitä tulee vakio:

G (x, y) = - 2x

Samoin osittainen johdannainen g kuin ja, tekeminen x vakio, johtuu funktiosta h-

H (x, y) = -2y

Harjoitus 2 

Arvioida (1, 2) toiminnot f (x, y) ja G (x, y) harjoituksen 1. Tulkita tuloksia.

Ratkaisu

Arvot korvataan x = 1 ja y = 2 saada:

F (1,2) = -(1)² -(2)² + 6 = -5 + 6 = 1

Tämä on arvo, joka vie funktion f, kun arvioidaan tuolloin.

Toiminto f (x, y) Se on kahden dimensioinen pinta ja koordinaatti z = f (x, y) Se on kunkin parin toiminnan korkeus (X, y). Kun pari otetaan (1,2), Pinnan korkeus f (x, y) On Z = 1.

Toiminto G (x, y) = - 2x edustaa tasoa kolmiulotteisessa tilassa, jonka yhtälö on Z = -2x O hyvin -2x + 0 ja -z = 0.

Mainittu lentokone on kohtisuorassa tasoon XZ Ja käydä läpi pisteen (0, 0, 0). Kun arvioidaan x = 1 ja y = 2 niin Z = -2. Huomaa, että arvo z = g (x, y) Se on riippumaton muuttujalle osoitetusta arvosta ja.

Toisaalta, jos pinta leikkaa f (x, y) Koneen kanssa y = c, kanssa c vakio, sinulla on käyrä tasossa Zx- z = -x² - c² + 6.

Tässä tapauksessa johdannainen z -z kuin x samaan aikaan kuin osittainen johdannainen f (x, y) kuin x- d -d_x Z = ∂_xF .

Arvioitaessa parissa (x = 1, y = 2) Osittainen johdannainen siinä vaiheessa ∂_xF (1,2) Se tulkitaan käyrän tangentin kaltevuutena z = -x² + 2 asiaan (x = 1, y = 2) Ja tämän kaltevuuden arvo on -2.

Viitteet

1. Ayres, f. 2000. Laskeminen. 5DED. MC Graw Hill.
2. Funktion osittaiset johdannaiset useissa muuttujissa. Toipunut: Rakennus.Kisko.On.
3. Leithold, L. 1992. Laskenta analyyttisellä geometrialla. Harla, S.-Lla.
4. Purcell, E. J -., Varberg, D., & Rigdon, S. JA. (2007). Laskeminen. Meksiko: Pearson Education.
5. Gorostizaga J. C. Osittaiset johdannaiset. Palautettu: EHU.Eus
6. Wikipedia. Osittainen johdannainen. Palautettu: on.Wikipedia.com.