Lineaarinen laajentuminen mikä on, kaava ja kertoimet, esimerkki

Se Lineaarinen laajentuminen tapahtuu, kun objekti kokee laajentumisen lämpötilan vaihtelun vuoksi, pääasiassa yhdellä ulottuvuudella. Tämä johtuu materiaalin ominaisuuksista tai sen geometrisesta muodosta. 

Esimerkiksi langassa tai palkissa, kun lämpötila nousee pitkälle, joka kärsii suurimmasta muutoksesta lämmön laajentumisen takia.

Lintuja poseeraa johdoissa. Lähde: Pixabay.

Kaapelit, joissa edellisen luvun linnut ahven kärsivät venytyksestä, kun niiden lämpötila nousee; Sen sijaan he supistuvat, kun ne jäähtyvät. Samalla tavalla se tapahtuu esimerkiksi rautatien kiskojen muodostavien palkkien kanssa.

[TOC]

Mikä on lineaarinen laajentuminen?

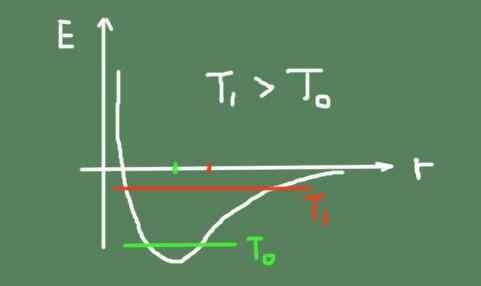Kaavio kemiallisen sidoksen energiasta verrattuna interatomiseen etäisyyteen. Lähde: Itse tehty.

Kiinteässä materiaalissa atomit ylläpitävät suhteellisia asentojaan enemmän tai vähemmän kiinteitä tasapainopisteen ympärille. Lämpöhäiriöiden vuoksi ne kuitenkin värähtelevät sen ympärillä.

Lämpötilaa nostamalla myös lämpö värähtely kasvaa, aiheuttaen väliaineen värähtelyasennot muutoksen. Tämä johtuu siitä, että linkkipotentiaali ei ole tarkalleen parabolinen ja siinä on epäsymmetria minimin ympärillä.

Alla on kuva, joka hahmottelee kemiallisen sidosenergian interatomisesta etäisyydestä riippuen. Näytetään myös kokonais värähtelyenergia kahdessa lämpötilassa, ja kuinka värähtelykeskus liikkuu.

Lineaarisen laajentumisen kaava ja sen kerroin

Lineaarisen dilaation mittaamiseksi aloitamme alkuperäisestä LE -pituudesta ja alkuperäisestä lämpötilasta t, jonka kohdetta haluat mitata laajentumistasi.

Oletetaan, että tämä esine on palkki, jonka pituus on L ja poikkileikkauksen mitat ovat paljon alhaisemmat kuin L.

Voi palvella sinua: Välitön kiihtyvyys: Mikä se on, miten se lasketaan ja harjoitukset

Ensinnäkin tälle objektille altistetaan ΔT -lämpötilan variaatio, niin että objektin lopullinen lämpötila, kun lämpötasapaino on määritetty lämmönlähteellä, on t '= t+ Δt.

Tämän prosessin aikana objektin pituus on myös muuttunut uuteen arvoon l '= l + ΔL, missä ΔL on pituuden vaihtelu.

Lineaarinen laajentumiskerroin a määritellään suhteeksi pituuden suhteellisen vaihtelun välillä lämpötilan variaatioyksikköä kohti. Seuraava kaava määrittelee lineaarisen laajentumiskertoimen α-

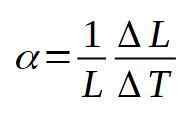Useimmissa tapauksissa, α Sillä on vakioarvo lämpötilojen välillä (t - Δt) ja (t + Δt).

Lineaarisen laajentumiskertoimen mitat ovat lämpötilan mitat.

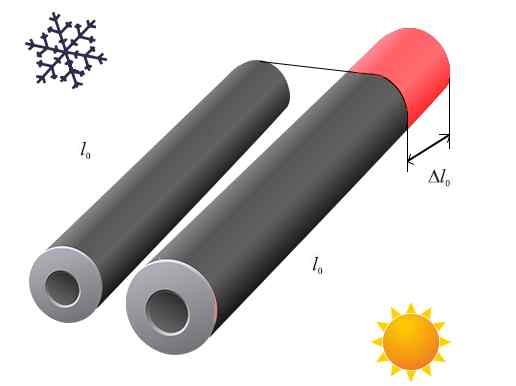
Lämpötila lisää putken muotoisten kiintoaineiden pituutta. Tätä kutsutaan lineaariseksi dilaatioksi. Lähde: Lafer.com

Lineaarinen dilaatiokerroin erilaisille materiaaleille

Seuraavaksi annamme luettelon lineaarisesta dilaatiokertoimesta joillekin tyypillisille materiaaleille ja elementeille. Kerroin lasketaan normaalissa ilmakehän paineessa, joka perustuu ympäristön lämpötilaan 25 ° C; ja sen arvoa pidetään vakiona AT: n alueella 100 ° C.

Lineaarinen dilaatiokerroinyksikkö on (° C)^-1.

- Teräs: α = 12 ∙ 10^-6 (° C)^-1

- Alumiini: α = 23 ∙ 10^-6 (° C)^-1

- Kulta: α = 14 ∙ 10^-6 (° C)^-1

- Kupari: α = 17 ∙ 10^-6 (° C)^-1

- Messinki: α = 18 ∙ 10^-6 (° C)^-1

- Rauta: α = 12 ∙ 10^-6 (° C)^-1

- Lasi: α = (7 - 9) ∙ 10^-6 (° C)^-1

- Elohopea: α = 60,4 ∙ 10^-6 (° C)^-1

- Kvartsi: α = 0,4 ∙ 10^-6 (° C)^-1

- Timantti: α = 1,2 ∙ 10^-6 (° C)^-1

- Lyijy: α = 30 ∙ 10^-6 (° C)^-1

Se voi palvella sinua: Konvektion lämmönsiirto (esimerkeillä)

- Tammipuu: α = 54 ∙ 10^-6 (° C)^-1

- PVC: α = 52 ∙ 10^-6 (° C)^-1

- Hiilikuitu: α = -0.8 ∙ 10^-6 (° C)^-1

- Betoni: α = (8 - 12) ∙ 10^-6 (° C)^-1

Useimmat materiaalit venyvät lämpötilan nousun myötä. Jotkut erityiset materiaalit, kuten hiilikuitu kutistuvat lämpötilan nousun myötä.

Ratkaistu esimerkki lineaarisesta laajenemisesta

Esimerkki 1

Kuparikaapeli ripustetaan kahden pylvään väliin, ja sen pituus viileässä päivässä 20 ° C: ssa on 12 m. Laske sen pituuden arvo kuumana päivänä 35 ° C: ssa.

Ratkaisu

Alkaen lineaarisen laajentumiskertoimen määritelmästä ja tietäen, että kuparin kannalta tämä kerroin on arvoinen: α = 17 ∙ 10^-6 (° C)^-1

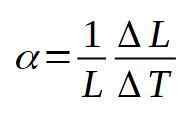
Pituuden lisääntyminen annetaan: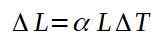

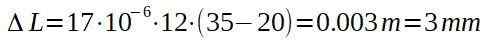
Kuparikaapeli lisääntyy sen pituudessa, mutta tämä on vain 3 mm. Eli kaapeli siirtyy 12 000 m: n olevan 12,003 metriä.

Esimerkki 2

Seppä, alumiinipalkki poistuu uunista 800 celsiusastetta, mitattuna 10,00 metrin pituiseksi. Kun se jäähtyy 18 celsiusasteen ympäristön lämpötilaan, määritä palkin pituus.

Ratkaisu

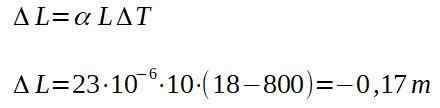
Toisin sanoen, kun palkki on kylmä, on kokonaispituus:

9,83 m.

Esimerkki 3

Teräksen niitit on halkaisija 0.915 cm. Alumiinilevylle tehdään 0,910 cm reikä. Tämä on alkuperäiset halkaisijat, kun ympäristön lämpötila on 18 ° C.

Millä minimilämpötilalla levyä tulisi lämmittää siten, että niitti kulkee reiän läpi? Tämän tavoitteena on, että kun rauta palaa huoneenlämpötilaan, niitti säädetään levylle.

Voi palvella sinua: Parallegrammimenetelmä: Esimerkkejä, ratkaisut harjoitukset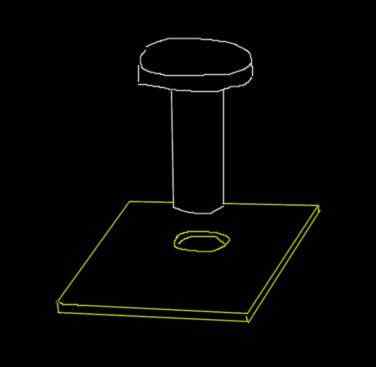Kuva esimerkiksi 3. Lähde: Itse tehty.

Ratkaisu

Vaikka levy on alue, olemme kiinnostuneita reiän halkaisijan laajentumisesta, joka on yhden dimensioinen määrä.

Soitetaan D_{0 -} alumiinilevyn alkuperäiseen halkaisijaan ja D, joka on kerran lämmitetty.

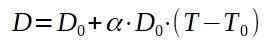
Lopullisen lämpötilan T puhdistaminen, sinulla on:

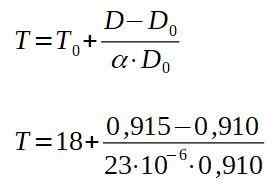
Edellisten toimintojen tulos on 257 ° C, mikä on vähimmäislämpötila, jossa levy on lämmitettävä siten, että niitti kulkee reiän läpi.

Esimerkki 4

Edellisen harjoituksen niitti ja plakki sijoitetaan yhteen uuniin. Määritä missä vähimmäislämpötilassa uunin on oltava niin, että teräs niitti kulkee alumiinilevyn reikän läpi.

Ratkaisu

Tässä tapauksessa sekä niitti että reikä viivästyvät. Mutta teräsulkailukerroin on α = 12 ∙ 10^-6 (° C)^-1, Kun taas alumiini on α = 23 ∙ 10^-6 (° C)^-1 .

Sitten etsimme lopullista lämpötilaa t siten, että molemmat halkaisijat osuvat.

Jos soitamme 1 niitille ja 2 alumiinilevylle, etsimme lopullista lämpötilaa t siten, että d₁ = D₂.

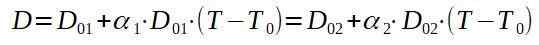
Jos puhdistamme lopullisen lämpötilan t, meillä on:

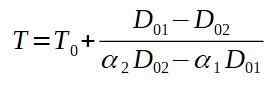
Seuraavaksi asetamme vastaavat arvot.

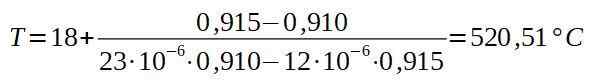
Johtopäätös on, että uunin on oltava vähintään 520,5 ° C niin, että niitti kulkee alumiinilevyn reiän läpi.

Viitteet

1. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. Kuudes painos. Prentice Hall. 238-249.
2. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. Mac Graw Hill. 422-527.