Halkaisijaltaan symbolit ja kaavat, miten se otetaan, kehä

Hän halkaisija Se on suora viiva, joka kulkee suljetun litteän käyrän tai kuvion läpi kahdessa tai kolmessa ulottuvuudessa ja liittyy myös sen vastakkaisiin pisteisiin. Se on yleensä ympyrä (litteä käyrä), ympyrä (litteä kuva), pallo tai suora pyöreä sylinteri (kolmiulotteiset esineet).

Vaikka kehä ja ympyrä pidetään yleensä synonyymeinä, molemmat termit ovat eroja. Ympyrä on suljettu käyrä, joka sulkee ympyrään, joka täyttää tilanteen, että minkä tahansa pisteiden ja keskuksen välinen etäisyys on sama. Tämä etäisyys ei ole kukaan muu kuin kehän säde. Sen sijaan ympyrä on tasainen kuva, jota ympärysmitta rajoittaa.

Kuvio 1. Polkupyörien halkaisija on tärkeä ominaisuus sen suunnittelussa. Lähde: Pixabay.

Ympyrän, ympyrän ja pallon tapauksessa halkaisija on suora segmentti, joka sisältää vähintään kolme pistettä: keskusta plus kaksi pistettä kehän tai ympyrän reunan tai pallon pinnan.

Ja suhteessa suorassa pyöreässä sylinterissä halkaisija viittaa poikkileikkaukseen, joka yhdessä korkeuden kanssa ovat sen kaksi ominaisparametria.

Ympyrän halkaisija ja ympyrä, jota symboloidaan Ø tai yksinkertaisesti kirjain "d" tai "d", liittyy sen kehään, muotoon tai pituuteen, jota on merkitty L -kirjaimella:

L = π.D = π. jompikumpi

Aina kun sinulla on kehä, sen pituuden ja halkaisijan välinen osuus on irrationaalinen luku π = 3.14159 ..., tällä tavalla:

π = l/d

[TOC]

Kuinka saada halkaisija?

Kun kehän tai ympyrän piirtäminen on saatavana tai suoraan pyöreä esine, kuten esimerkiksi valuutta tai rengas, on erittäin helppo ottaa halkaisija sääntöllä. Sinun on vain varmistettava, että säännön reunalla samanaikaisesti on kaksi kehän ja saman keskipistettä.

Voi palvella sinua: algebrallinen

Kaliiperi, Vernier tai Kingin jalka on erittäin sopiva ulkoisten ja sisähalkaisijoiden mittaamiseen kolikoissa, vanteissa, renkaissa, muttereissa, putkissa ja muissa.

Kuva 2. Vernier digitaalinen mittaa kolikon halkaisija. Lähde: Pixabay.

Jos objektin tai sen piirustuksen sijasta sinulla on tietoja, kuten radio R -, Sitten kertomalla 2: lla, sinulla on halkaisija. Ja jos kehän pituus tai kehä tunnetaan, halkaisija voidaan myös tietää, puhdistuksella:

D = 2.R -
D = l / π

Toinen tapa saada halkaisija on tuntea ympyräalue, pallomainen pinta, sylinterin poikkileikkaus, tämän tai sylinterin tai sylinterin tilavuudet. Kaikki riippuu siitä, mikä geometrinen luku on. Esimerkiksi halkaisija on mukana seuraavilla alueilla ja tilavuuksilla:

-Ympyräalue: π.(D/2)²
-Pallomainen pinta -ala: 4π.(D/2)²
-Pallon tilavuus: (4/3) π.(D/2)³
-Suora pyöreä sylinteritilavuus: π.(D/2)².H (H on sylinterin korkeus)

Vakiona leveät luvut

Ympyrä on vakioleveä litteä kuva, koska missä tahansa se näyttää, leveys on halkaisija D. On kuitenkin muitakin vähemmän tunnettuja lukuja, joiden leveys on myös vakio.

Katsotaanpa ensin, mitä kuvan leveys ymmärretään: se on kahden rinnakkaisviivan välinen etäisyys -tukevat asemat -mikä puolestaan ​​on kohtisuorassa annettuun suuntaan ja että vangitsee kuvan, kuten vasemmassa kuvassa on esitetty:

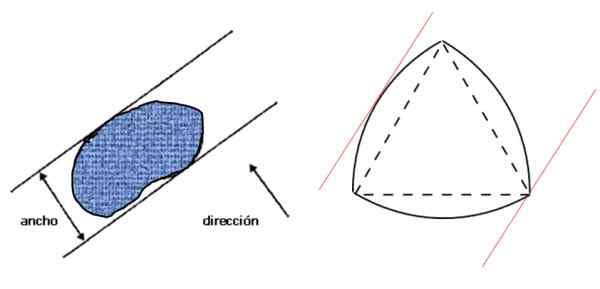Kuva 3. Minkä tahansa litteän kuvan (vasen) ja Reuleaux -kolmion leveys, vakio leveä kuva (oikea). Lähde: f. Zapata.

Sitten oikealla on Reuleaux -kolmio, joka on vakio leveä kuva ja joka täyttää vasemmassa kuvassa määritellyn tilanteen. Jos hahmon leveys on D, sen kehä antaa Barbierin lause:

Voi palvella sinua: Amorfisten lukujen likimääräinen mittaus: Esimerkki ja liikunta

L = π.D -d

San Franciscon kaupungin viemärit Kaliforniassa on muotoiltu Reuleaux'n kolmioksi, nimeltään saksalainen insinööri Franz Reuleaux (1829 - 1905). Tällä tavalla tapas ei voi pudota reikään ja käyttää vähemmän materiaalia niiden valmistukseen, koska niiden alue on pienempi kuin ympyrän:

A = (1- √3).πd² = 0.705.D -d²

Kun ympyrä varten:

A = π.(D/2)² = (π/4) d²= 0.785.D -d²

Mutta tämä kolmio ei ole ainoa vakio leveä luku. Puhelut voidaan rakentaa Reuleaux -polygonit muiden monikulmioiden kanssa, joilla on pariton sivunumero.

Ympärysmitta

Seuraavassa luvussa on kehän elementit, jotka on määritelty seuraavasti:

Köysi: linjasegmentti, joka yhdistää kehän kaksi pistettä. Kuvassa on köyttä, joka liittyy pisteisiin C ja D, mutta äärettömät jouset voidaan jäljittää, jotka ainutlaatuiset ympäristön pari pistettä.

Halkaisija: Se on köysi, joka kulkee keskuksen läpi, yhdistäen kehän kaksi pistettä keskustaan ​​tai. Se on kehän pisin köysi, tästä syystä sitä kutsutaan "suureksi köysiksi".

Radio: linjasegmentti, joka liittyy keskustaan ​​millä tahansa kehän pisteellä. Sen arvo, kuten halkaisija, on vakio.

Ympärysmitta: Se on joukko pisteitä, jotka rinnastavat tai.

Keula: Se on määritelty kehäsegmentiksi, jonka kaksi radiota on rajattu (ei piirretty kuvaan).

Kuva 4. Kehän osia, mukaan lukien halkaisija, joka kulkee keskuksen läpi. Lähde: Wikimedia Commons.

- Esimerkki 1

Esitetty suorakulmio on 10 tuumaa pitkä, joka käämiessä se muodostaa suoran pyöreän sylinterin, jonka halkaisija on 5 tuumaa. Vastaa seuraaviin kysymyksiin:

Se voi palvella sinua: toisiaan poissulkevat tapahtumat: ominaisuudet ja esimerkit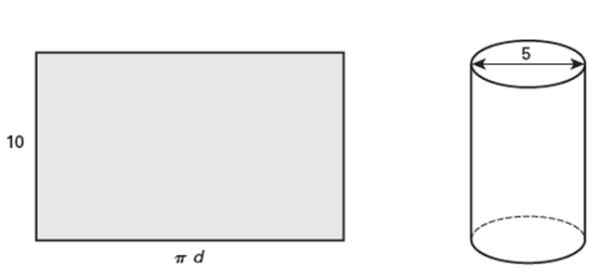Kuva 5. Valssatusta suorakulmiosta tulee suora pyöreä sylinteri. Lähde: Jiménez, R. Matematiikka II. Geometria ja trigonometria. Toinen. Painos. Pearson.

a) mikä on putken ääriviivat?
b) Etsi suorakulmioalue
c) Laske sylinterin ristikkäinen alue.

Liittää jhk

Putken muoto on l = π.D = 5π plg = 15.71 PLG.

Ratkaisu b

Suorakulmioalue on Pohja x korkeus, Koska pohja L on jo laskettu ja korkeus on 10 PLG lausunnon mukaan: siksi:

A = 15.71 plg x 10 plg = 157.1 plg².

Liuos C

Lopuksi pyydetty alue lasketaan seuraavasti:

A = π.(D/2)² = (π/4) d² = (π/4) x (5 PLG)²= 19.63 PLG².

- Esimerkki 2

Laske kuvan 5A varjostettu alue. Neliöllä on sivu L.

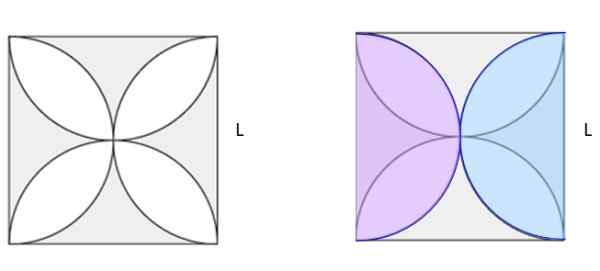Kuva 6. Etsi varjostettu alue vasemmasta kuvasta. Jiménez, r. Matematiikka II. Geometria ja trigonometria. Toinen. Painos. Pearson.

Ratkaisu

Kuviossa 5b on piirretty kaksi identtistä koko, kokoinen koko vaaleanpunaisissa ja sinisissä värissä, päällekkäin alkuperäisessä kuvassa. Heidän välillä he tekevät täydellisen ympyrän. Jos neliön neliö lasketaan ja ympyrän pinta -ala on vähennetty, se tekee kuvan 5b varjostetusta pinta -alasta. Ja näyttää hyvältä, osoittautuu, että se on puolet varjostetusta alueesta 5A: ssa.

-Alue -aukio: l²
-Puoli -ympyrän halkaisija: L
-Ympyräalue: π.(L/2)²= (π/4) l²
-Alueiden ero = puolet varjostetusta alueesta =

Lens² - (π/4) l² = [(4 - π)/4] l²= 0.2146 l²

-Varjostettu alue = 2 x 0.2146 l²= 0.4292L2

Kuinka monta halkaisijaa kehällä on?

Äärettömät halkaisijat voidaan piirtää ympyrään, ja mikä tahansa niistä mittaa samat.

Viitteet

1. Antonio. Reuleaux -kolmiot ja muut vakioleveyskäyrät. Palautettu: levittäjät.com.
2. Baldor, a. 2002. Litteä ja tila ja trigonometriageometria. Kulttuuriryhmä.
3. Jiménez, r. Matematiikka II. Geometria ja trigonometria. Toinen. Painos. Pearson.
4. Wikipedia. Reuleaux -kolmio. Palautettu: se on.Wikipedia.org.
5. Wolfram Mathworld. Halkaisija. Toipunut: MathWorld.Susi.com.