Hiukkasjärjestelmän dynamiikka, harjoitukset

Se Hiukkasjärjestelmän dynamiikka Se koostuu Newtonin lakien soveltamisesta liikkeestä hiukkasjoukkoon, joka voidaan olla hienovarainen (hiukkaset voidaan laskea) tai olla osa laajennettua esinettä, tässä tapauksessa järjestelmä on jatkuva.

Hiukkasjärjestelmän liikkumisen selittämiseksi on hankalaa analysoida kutakin erikseen ja nähdä, mitkä voimat siihen toimivat. Sen sijaan määritetään sarjan edustava kohta, nimeltään Massakeskus.

Massikeskuksen liikkumisen kuvaaminen tarjoaa erittäin menestyvän panoraaman sarjan globaalista liikkeestä, sallii myös soveltaa Newtonin lakeja, jotka ovat analogisia siihen, kun esinettä pidetään hiukkasena ilman mittoja.

Tämä viimeinen malli, nimeltään hiukkasmalli, On hyvä kuvata käännöksiä ja myös silloin, kun objektin mittoja ei tarvitse harkita. Mutta tavalliset esineet ovat kokoisia, ja jos niillä on myös kiertoliike, on tarpeen ottaa huomioon kohdat, joissa voimat kohdistetaan.

[TOC]

Esimerkit

Maa ja kuu

Maa- ja kuun kuva

Joukko erillisiä hiukkasia m₁, m₂, m₃... Se lopulta liikkuu koordinaattijärjestelmän alkuperän suhteen, johtuen siitä johtuen siitä, että niihin liittyvä voima on hyvä esimerkki hiukkasjärjestelmästä.

Maata voidaan pitää yhtenä hiukkasena ja kuun toisena, sitten molemmat muodostavat kahden hiukkasen järjestelmän auringon painovoiman vaikutuksesta.

Laajennetut esineet

Henkilöä, eläintä tai mikä tahansa ympäristökohde, voidaan pitää myös hiukkasjärjestelmänä, vain että nämä ovat niin pieniä, että ei voida laskea yksi kerrallaan. Tämä on jatkuva järjestelmä, mutta ottaen huomioon tietyt näkökohdat, sen hoito on sama kuin huomaamaton järjestelmä.

Se voi palvella sinua: mikä on koulutuksen entalpia? (Harjoituksilla)

Tässä ovat yksityiskohdat.

Hiukkasjärjestelmän massakeskus

Hiukkasjärjestelmän tutkimuksen aloittamiseksi sinun on löydettävä massakeskus (cm), mikä on piste, jossa järjestelmän koko massa on keskittynyt.

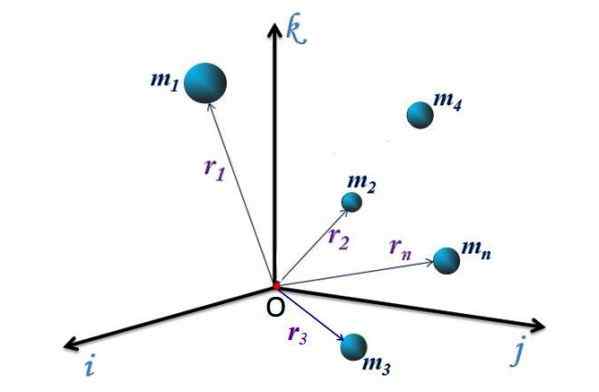
Kuvio 1. Hiukkasjärjestelmä XYZ -vertailujärjestelmässä. Lähde: f. Zapata.

Kuvion 1 erilliselle järjestelmälle, n Hiukkaset, jokaisella on sijaintivektori, joka on suunnattu alkuperästä tai koordinaattijärjestelmästä pisteeseen P (x, y, z), missä hiukkas. Nämä vektorit merkitään nimellä r -₁, r -₂, r -₃.. r -_n.

CM -koordinaatit lasketaan seuraavilla yhtälöillä:

Missä jokainen sarjan massasta on esitetty m₁, m₂, m₃... m_n. Huomaa, että summa ∑ m_Yllyttää Se vastaa sarjan kokonaismassaa m. Jos järjestelmä on jatkuva, yhteenvedot korvataan integraaleilla.

Jokaista kohtisuoraosoitteita edustaa yksikkövektorit Yllyttää, J - ja k -k -, Siksi CM -sijaintivektori, merkitty r -_Cm, Se voidaan ilmaista:

r -_Cm = x_Cm Yllyttää + ja_Cm J - + z -z_Cm k -k -

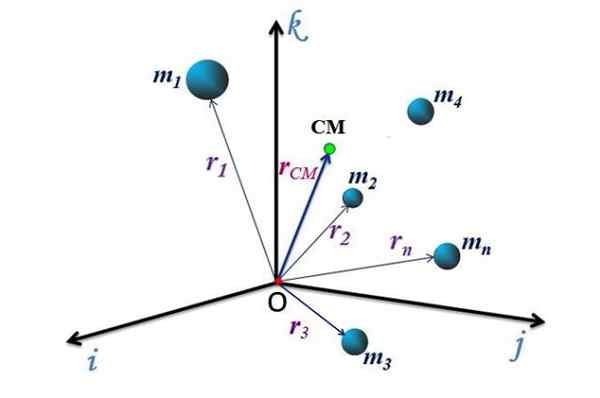Kuva 2. Hiukkasjärjestelmän massakeskus sijainti. Lähde: f. Zapata.

Cm -liike

Kun massikeskuksen sijainti on tiedossa, liikkeen tunnettuja yhtälöitä käytetään. CM: n nopeus on ensimmäinen johdettu sijainnista ajan suhteen:

Tässä tapauksessa järjestelmässä on kokonaismäärä liike P joka lasketaan järjestelmän kokonaismassan ja massan keskuksen nopeuden tuloksena:

Se voi palvella sinua: Fyysinen etenemissuunta: Ominaisuudet, tyypit, esimerkit ja harjoitukset

P = M ∙v_Cm

Vaihtoehtoisesti järjestelmän järjestelmän kokonaismäärä voidaan laskea suoraan:

P = m₁v₁ + m₂v₂ + m₃v₃ +.. . = ∑ m_Yllyttää v_Yllyttää

Kun taas CM: n kiihtyminen on johdettu nopeus:

Vahvuus CM: llä

Hiukkasjärjestelmään vaikuttavat voimat voivat olla:

• Sisäiset voimat samojen hiukkasten välisistä vuorovaikutuksista johtuen.
• Ulkoiset voimat, jotka aiheuttavat järjestelmän ulkopuoliset edustajat.

Koska sisäiset voimat esitetään pareittain, samalla suuruudella ja suunnassa, mutta vastakkaiset aistit, Newtonin kolmannen lain mukaan on täytettävä, että:

∑ F_int = 0 -

Siksi sisäiset voimat eivät muuta kokonaisuuden liikettä, mutta ne ovat erittäin tärkeitä sisäisen energian määrittämiseksi.

Jos järjestelmä on eristetty ja Newtonin ensimmäisen lain mukaan ulkoisia voimia ei ole, massikeskus on levossa tai liikkuu yhtenäisellä suorakulmioliikkeellä. Muutoin massakokemuksen keskipiste kiihtyvyydestä:

∑ F_alanumero = M ∙-lla_Cm

Missä m on järjestelmän kokonaismassa. Aikaisempi yhtälö voidaan kirjoittaa näin:

Ja se tarkoittaa, että ulkoinen voima vastaa liikkeen määrän väliaikaista vaihtelua, toinen tapa ilmaista Newtonin toinen laki ja sama, jota kuuluisa englantilainen fyysikko käyttää kirjassaan Periaate.

Liikuntaa

2 hiukkasjärjestelmän massakeskus on x -akselilla tietyllä hetkellä, asennossa x = 2.0 m ja liikkuu nopeudella 5.0 m/s samaan suuntaan ja positiivisesti. Jos yksi hiukkasista on alkuperässä ja toinen, massa 0.1 kg, on levossa x = 8.0 m, laske:

Voi palvella sinua: Diamagnetismi: Materiaalit, sovellukset, esimerkit

a) Hiukkasen massa, joka on alkuperässä.

b) Järjestelmäliikkeen määrä

c) Mikä nopeus hiukkas on alkuperässä?

Liittää jhk

Massikeskuksen sijainnin yhtälöstä:

r -_Cm = x_Cm Yllyttää + ja_Cm J - + z -z_Cm K = 2.0 m Yllyttää

Koska CM: llä on vain X -koordinaatti, käytetään ensimmäistä aikaisemmin annettua trioyhtälöä:

Koordinaatit korvataan nyt, jos hiukkanen on merkitty alkuperässä, kuten numero 1 ja muut, kuten numero 2, numeeriset tiedot ovat:

x₁ = 0 m, x₂ = 8.0 m, m₂ = 0.1 kg, x_Cm = 2.0 m

Pysyminen:

= 0.3kg

Ratkaisu b

Järjestelmän liikkeen määrä lasketaan:

P = M ∙v_Cm

Kokonaismassa m on yhtä suuri kuin:

M = 0.3 kg + 0.1 kg = 0.4 kg

Siksi:

P = 0.4 kg ∙ 5.0 m/s Yllyttää = 2 kg.neiti Yllyttää

Liuos C

Yhtälö P kahden osapuolen järjestelmästä se tyhjentää v₁, Koska muut tiedot tunnetaan, koska lausunnossa sanotaan, että hiukkas 2 on levossa, siksi:

v₂ = 0 - 

JA P Se on yksinkertaisesti kuin:

P = m₁v₁

v₁ = P / m₁ = 2 kg.neiti Yllyttää / 0.3kg = 6.67 m/s Yllyttää

Viitteet

1. Duke University. Hiukkasten järjestelmät. Palautettu: WebHome.Pala.Herttua.Edu.
2. Rex, a. 2011. Fysiikan perusteet. Pearson.
3. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1. Pearson.
4. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Osa 1. Seitsemäs. Ed. Cengage -oppiminen.
5. Tipler, P. (2006) Tieteen ja tekniikan fysiikka. 5. ed. Osa 1. Toimitus palautti.