Hypergeometrinen jakaumakaavat, yhtälöt, malli

Se hypergeometrinen jakauma Se on hienovarainen tilastollinen funktio, joka on riittävä laskemaan todennäköisyys satunnaiskokeissa kahdella mahdollisella tuloksella. Sovellettavaksi tarvittava ehto on, että se on pieni populaatio, jossa uuttoja ei korvata ja todennäköisyydet eivät ole vakioita. 

Siksi, kun väestöelementti valitaan tietämään tietyn ominaisuuden tulos (tosi tai väärä), samaa elementtiä ei voida valita uudelleen.

Kuvio 1. Tällaisten ruuvien populaatiossa on varmasti viallisia näytteitä. Lähde: Pixabay.

Varmasti seuraava valittu elementti saa siis todennäköisemmin todellisen tuloksen, jos edellisellä elementillä oli negatiivinen tulos. Tämä tarkoittaa, että todennäköisyys on vaihteleva siinä määrin, että näytteen elementit uutetaan.

Hypergeometrisen jakauman tärkeimmät sovellukset ovat: laadunvalvonta prosesseissa, joissa on vähän populaatiota, ja todennäköisyyksien laskeminen satunnaisissa peleissä.

Mitä tulee matemaattiseen funktioon, joka määrittelee hypergeometrisen jakauman, tämä koostuu kolmesta parametrista, jotka ovat:

- Väestöelementtien luku (n)

- Näytteen koko (m) 

- Koko populaation tapahtumien lukumäärä, jolla on suotuisa (tai epäsuotuisa) tulos tutkituista ominaisuuksista (n).

[TOC]

Kaavat ja yhtälöt

Hypergeometrinen jakautumiskaava antaa todennäköisyyden P mitä x Tiettyjen ominaisuuksien suotuisat tapaukset tapahtuvat. Tapa kirjoittaa se matemaattisesti, yhdistelmälukuista riippuen on:

Edellisessä ilmaisussa N, n ja m Ne ovat parametreja ja x itse muuttuja. 

-Kokonaisväestö on N.

-Tietyn binaarisen ominaisuuden positiivisten tulosten lukumäärä kokonaispopulaation suhteen on n.

-Näytteen lukumäärä on m.

Tässä tapauksessa, X Se on satunnaismuuttuja, joka ottaa arvoa x ja P (x) osoittaa esiintymisen todennäköisyyden x suotuisat tutkitun ominaisuuden tapaukset.

Tärkeät tilastolliset muuttujat

Muita tilastollisia muuttujia hypergeometriseen jakaumaan ovat:

- Puoli μ = m*n/n

- Varianssi σ^2 = m*(n/n)*(1-n/n)*(n-m)/(n-1)

- Tyypillinen poikkeama σ joka on varianssin neliöjuuri.

Malli ja ominaisuudet 

Päästäksesi hypergeometriseen jakautumismalliin, se perustuu saamisen todennäköisyyteen x suotuisat tapaukset koonäytteessä m. Tämä näyte sisältää elementtejä, jotka täyttävät tutkittavan kiinteistön, ja elementtejä, jotka eivät.

Muistakaamme se n edustaa suotuisten tapausten lukumäärää koko väestössä N kohteet. Sitten todennäköisyys lasketaan näin:

Voi palvella sinua: vektoritila: pohja ja mitta, aksioomit, ominaisuudet

P (x) = (# tavoista saada x# epäonnistuneilla tavoilla)/(# valintatavat)

Edellä esitetyn yhdistelmälukujen muodossa, seuraavat todennäköisyyden jakautumismallit saavutetaan:

Hypergeometrisen jakauman pääominaisuudet

Ovat seuraavat:

- Otoksen on aina oltava pieni, vaikka populaatio on suuri.

- Näytteen elementit uutetaan yhdestä sisällyttämättä niitä uudelleen väestöön.

- Tutkittava ominaisuus on binaarinen, ts. Se voi ottaa vain kaksi arvoa: 1 jompikumpi 0 -, O hyvin TOTTA jompikumpi väärennetty.

Jokaisessa vaiheen uuttamisvaiheessa todennäköisyys muuttuu aiempien tulosten mukaan.

Lähestymistapa binomiaalisesti

Toinen hypergeometrisen jakauman ominaisuus on, että siihen voidaan lähestyä binomijakaumaa, nimeltään Bi, Niin kauan kuin väestö N olla suuri ja vähintään 10 kertaa suurempi kuin näyte m. Tässä tapauksessa se olisi niin:

P (n, n, m; x) = bi (m, n/n, x)           

Niin kauan kuin n on suuri ja n> 10m

Esimerkit

Esimerkki 1

Oletetaan, että kone, joka tuottaa ruuveja ja kertyneitä tietoja. Sitten n = 500 ruuviruuvissa virheiden lukumäärä on:

N = 500 * 1/100 = 5

Todennäköisyydet hypergeometrisen jakauman kautta

Oletetaan.

Todennäköisyys, että näytteen ruuvi (x = 0) ei ole viallinen, ei ole 52,63%. Tämä tulos saavutetaan käytettäessä hypergeometristä jakautumistoimintoa:

P (500, 5, 60; 0) = 0,5263

Todennäköisyys, että x = 3 näytteen ruuvit jättävät viallisen, on: P (500, 5, 60; 3) = 0,0129.

Toisaalta todennäköisyys, että näytteen kuusikymmentäluvun x = 4 ruuvit ovat puutteellisia, on: P (500, 5, 60; 4) = 0,0008.

Lopuksi, todennäköisyys, että x = 5 ruuvia kyseisessä näytteessä tulee virheeseen, on: P (500, 5, 60; 5) = 0.

Mutta jos haluat tietää todennäköisyyden, että kyseisessä näytteessä on enemmän kuin 3 viallista ruuvia, on saatava kertynyt todennäköisyys, lisäämällä:

P (3)+P (4)+P (5) = 0,0129+0,0008+0 = 0,0137.

Tämä esimerkki on esitetty kuvassa 2, joka on saatu käyttämällä Geogebra Laajakäyttöinen ilmainen ohjelmisto kouluissa, instituutioissa ja yliopistoissa.

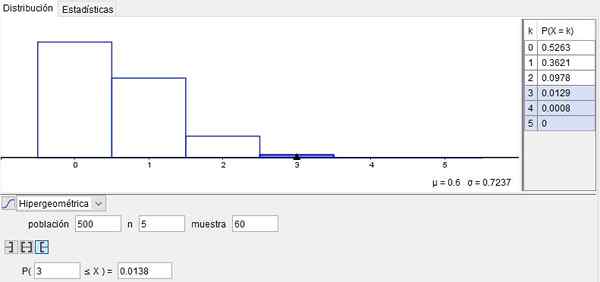Kuva 2. Esimerkki hypergeometrisesta jakautumisesta. Valmistettu f. Zapata geogebralla.

Esimerkki 2

Espanjalaisella kannella on 40 korttia, joista 10 on kultaa ja loput 30: lla ei ole sitä. Oletetaan.

Voi palvella sinua: Keskeinen symmetria: Ominaisuudet, esimerkit ja harjoitukset

Jos x on kullan lukumäärä, joka on läsnä 7 poistetussa kortissa, niin todennäköisyys, että X Oroos on 7 kortin uuttamisessa, annetaan hypergeometrisella jakaumalla P (40,10,7; x).

Tarkastellaan tätä: Lasketaan todennäköisyys, että 4 kultaa on 4 kortin uuttamisessa, käytämme hypergeometristä jakautumiskaavaa seuraavilla arvoilla:

Ja tulos on: 4,57% todennäköisyys.

Mutta jos haluat tietää todennäköisyyden saada yli 4 korttia, meidän on lisättävä:

P (4)+P (5)+P (6)+P (7) = 5,20%

Ratkaisut

Seuraavat harjoitukset on tarkoitus havainnollistaa ja omaksua käsitteitä, jotka on esitetty tässä artikkelissa. On tärkeää, että lukija yrittää ratkaista ne yksin, ennen kuin tarkastellaan ratkaisua.

Harjoitus 1

Ennaltaehkäisevä tehdas on havainnut, että jokaisesta tietyn koneen tuottamasta 1000 kondomista 5 on viallinen. Laadunvalvonnan suorittamiseksi 100 kondomia otetaan satunnaisesti ja erä hylätään, jos on ainakin yksi tai useampi viallinen. Vastaa:

a) minkä mahdollisuuden on oltava 100 erä hylätty?

b) Onko tämä laadunvalvontakriteeri tehokas?

Ratkaisu

Tässä tapauksessa ilmestyy erittäin suuria yhdistelmälukuja. Laskenta on vaikeaa, ellei riittävä tietokonepaketti ole käytettävissä.

Mutta koska se on suuri populaatio ja otos on kymmenen kertaa vähemmän kuin kokonaispopulaatio, voit käyttää lähestymistapaa hypergeometriseen jakautumiseen binomijakauman vuoksi:

P (1000,5,100; x) = bi (100, 5/1000, x) = bi (100, 0.005, x) = c (100, x)*0.005^x (1-0.005)^(100-x)

Edellisessä ilmaisussa C (100, x) Se on yhdistelmänumero. Silloin Hayan todennäköisyys useampi kuin yksi viallinen lasketaan seuraavasti:

P (x> = 1) = 1 - bi (0) = 1-.6058 = 0.3942

Se on erinomainen lähestymistapa verrattuna arvoon, joka saadaan hypergeometristä jakaumaa sovellettaessa: 0.4102

Voidaan sanoa, että 40%: n todennäköisyys, paljon 100 ennaltaehkäisevää ennaltaehkäisyä tulisi hylätä, mikä ei ole kovin tehokas.

Mutta koska se on hiukan vähemmän vaativa laadunvalvontaprosessissa ja hylkää.

Harjoitus 2

Muovinen taco -kone toimii siten, että jokaisesta kymmenestä kappaleesta on muodonmuutos. 5 -kappaleen näytteessä, että mahdollisuus on oltava yhden kappaleen viallinen.

Ratkaisu

Väestö: n = 10

Voi palvella sinua: Pythagorean -identiteetit: esittely, esimerkki, harjoitukset

Numero n viallinen jokaiselle n: n = 1

Näytteen koko: M = 5

P (10, 1, 5; 1) = C (1,1)*C (9,4)/C (10,5) = 1*126/252 = 0.5

Siksi on 50% todennäköisyys, että viidessä näytteessä taco tulee epämuodostuneeksi.

Harjoitus 3

Nuorten lukioiden kokouksessa on 7 naista ja 6 herraa. Tyttöjen keskuudessa 4 tutkimus humanistista ja 3 tiedettä. Poikaryhmässä 1 tutkii humanistisia ja 5 tieteitä. Laske seuraava:

a) Kolmen tytön satunnaisesti: Mitkä ovat todennäköisyys, että kaikki tutkimus humanistiset tieteet?.

b) Jos ystävätapaamiseen valitaan kolme osallistujaa: mitkä ovat kolme heistä sukupuolesta riippumatta, opiskele kolmea tai humanistisia tieteitä myös kaikki kolme?.

c) Valitse nyt kaksi satunnaista ystävää ja soita x satunnaismuuttujalle "humanististen tieteiden tutkijoiden lukumäärä". Määritä kahdesta valituista keskiarvosta tai odotetusta arvosta x ja varianssi σ^2.

Liittää jhk 

Väestö on tyttöjen kokonaismäärä: n = 7. Humanistiset tieteet ovat n = 4, kokonaismäärästä. Tyttöjen satunnainen näyte on M = 3.

Tällöin todennäköisyys, että nämä kolme ovat humanistisia tieteitä, annetaan hypergeometrisella funktiolla:

P (n = 7, n = 4, m = 3, x = 3) = c (4, 3) c (3, 0) / c (7, 3) = 0.1143

Sitten on 11.4%: n todennäköisyys, että kolme satunnaista chicas -tutkimusta humanistiset tieteet.

Ratkaisu b

Käytettävät arvot ovat:

-Väestö: n = 14

-Määrä, joka tutkii kirjaimia, on: n = 6 ja

-Näytteen koko: M = 3.

-Humanististen tieteiden opiskelevien ystävien lukumäärä: x

Tämän mukaan x = 3 tarkoittaa, että kolme tutkimusta humanistista, mutta x = 0 tarkoittaa, että yksikään ei tutki humanistisia tietoja. Todennäköisyys, että kolme tutkimus on sama, annetaan summalla:

P (14, 6, 3, x = 0) + P (14, 6, 3, x = 3) = 0.0560 + 0.1539 = 0.2099

Sitten meillä on 21% todennäköisyys, että satunnaisesti valitut kolme kokousjäsentä tutkivat samaa.

Liuos C

Täällä meillä on seuraavat arvot:

N = 14 ystävien väestöä, n = 6 humanististen tieteiden tutkivan väestön kokonaismäärä, näytteen koko on M = 2.

Toivottavasti on:

E (x) = m * (n/n) = 2 * (6/14) = 0.8572

Ja varianssi:

σ (x)^2 =  m*(n/n)*(1-N/n)*(n-m)/(n-1) = 2*(6/14)*(1-6/14)*(14-2)/(14 -1) =

= 2*(6/14)*(1-6/14)*(14-2)/(14-1) = 2*(3/7)*(1-3/7)*(12) (13)  = 0.4521

Viitteet

1. Erilliset todennäköisyysjakaumat. Toipunut: Biploot.USAL.On
2. Tilasto ja todennäköisyys. Hypergeometrinen jakauma. Haettu osoitteesta: ProjecodesCartes.org
3. Cdpye-Ugr. Hypergeometrinen jakauma. Palautettu: ugr.On
4. Geogebra. Klassinen geogebra, todennäköisyyslaskelma. Toipunut geogebrasta.org
5. Helppo testamentti. Ratkaistuja hypergeometrisiä jakeluharjoituksia. Palautettu: probafacil.com
6. Minitab. Hypergeometrinen jakauma. Haettu: tuki.Minitab.com
7. Vigon yliopisto. Tärkeimmät jakaumat. Toipunut: Anapg.verkkosivustot.Uvigo.On
8. Vituturi. Tilastot ja yhdistelmä. Haettu osoitteesta: vitur.netto
9. Weisstein, Eric W. Hypergeometrinen jakauma. Toipunut: MathWorld.Susi.com
10. Wikipedia. Hypergeometrinen jakauma. Palautettu: on.Wikipedia.com