Satunnainen koe -konsepti, näytetila, esimerkkejä

Siellä on puhetta satunnainen kokeilu Kun kunkin tietyn kokeen tulos on arvaamaton, vaikka tietyn tuloksen esiintymisen todennäköisyys voidaan vahvistaa.

On kuitenkin selvennettävä, että satunnaisen järjestelmän samaa tulosta ei ole mahdollista toistaa samat alkuperäiset parametrit ja olosuhteet kokeen kussakin tutkimuksessa.

Kuvio 1. Dice -käynnistys on satunnainen koe. Lähde: Pixabay.

Hyvä esimerkki satunnaisesta kokeesta on noppan käynnistäminen. Jopa kun huolehdit noppan käynnistämisestä samalla tavalla, jokaisessa yrityksessä saadaan arvaamaton tulos. Itse asiassa ainoa asia, joka voidaan vahvistaa, on, että tulos voi olla joitain seuraavista: 1, 2, 3, 4, 5 tai 6.

Valuutan lanseeraus on toinen esimerkki satunnaisesta kokeesta vain kahdella mahdollisella tuloksella: kasvot tai sinetti. Vaikka valuutta käynnistetään samasta korkeudesta ja samalla tavalla, mahdollisuuskerroin on aina läsnä, mikä johtaa epävarmuuteen jokaiselle uudelle yritykselle.

Satunnaisen kokeen vastakohta on deterministinen koe. Esimerkiksi tiedetään, että joka kerta, kun vesi keitetään merenpinnalla, kiehumislämpötila on 100 ºC. Mutta ei koskaan tapahdu, että samojen olosuhteiden ylläpitäminen on joskus 90 ºC, toinen 12 0ºC ja joskus 100 ºC.

[TOC]

Esimerkkitila

Satunnaisen kokeen kaikkien mahdollisten tulosten joukkoa kutsutaan esimerkkitila. Putken käynnistämisessä satunnaisessa kokeessa näytetila on:

D = 1, 2, 3, 4, 5, 6.

Valuutan käynnistämisen yhteydessä näytetila on:

M = kasvot, sinetti.

Tapahtuma tai tapahtuma

Satunnaisessa kokeessa a tapahtuma Se on tapahtuma tai ei tietyn tuloksen. Esimerkiksi valuutan lanseerauksen tapauksessa tapahtuma tai tapahtuma on oltava kallista.

Voi palvella sinua: homologiset puolet

Toinen tapahtuma satunnaisessa kokeessa voi olla seuraava: että noppaa käynnistyessä lukumäärä on alle kolme.

Jos tapahtuma tapahtuu, mahdollisten tulosten joukko on joukko:

E = 1, 2, 3

Tämä puolestaan ​​on avaruus- tai näytejoukon osajoukko:

M = 1, 2, 3, 4, 5, 6.

Esimerkit

Alla on joitain esimerkkejä, jotka kuvaavat yllä:

Esimerkki 1

Oletetaan, että kaksi kolikkoa heitetään, yksi toisensa jälkeen. Sitä pyydetään:

a) Ilmoita onko se satunnainen koe vai päinvastoin deterministinen koe.

b) Mikä on tämän kokeen näytetila?

c) Ilmoita koko tapahtuma A, joka vastaa kokeilua, on kasvo- ja leimatulos.

d) Laske todennäköisyys, että tapahtuma tapahtuu.

e) Lopuksi löydä todennäköisyys, että tapahtuma B: ei näytä tuloksesta.

Ratkaisu 

a) Se on satunnainen koe, koska ei ole mitään keinoa ennustaa, mikä on seurausta kahden kolikon käynnistämisestä.

b) Näytetila on joukko mahdollisia tuloksia:

S = (c, c), (c, s), (s, c), (s, s)

c) Tapahtumassa A voi olla seuraavat tulokset:

A = (c, s), (s, c)

d) Tapahtuman A todennäköisyys saadaan jakamalla sarjan A elementtien lukumäärä näytetilaa vastaavan joukon elementtien lukumäärän välillä:

P (a) = 2/4 = ½ = 0.5 = 50%

e) Mahdollisten tulosten joukko, joka vastaa tapahtumaa B (ei näy tuloksella) on:

Voi palvella sinua: täydellinen neliömäinen trinomial

B = (s, s)

Joten todennäköisyys, että tapahtuma B esiintyy esseessä, on suhde B: n mahdollisten tulosten lukumäärän välillä kokonaismäärän lukumäärän välillä:

P (b) = ¼ = 0.25 = 25%.

Esimerkki 2

Laukku sisältää 10 valkoista marmoria ja 10 mustaa marmoria. Pussista ne poistetaan satunnaisesti ja katsomatta kolmen marmorin sisällä peräkkäin. 

a) Määritä tämän satunnaisen kokeen näytetila.

b) Määritä tapahtumaa vastaavien tulosjoukko, joka on, että kokeen jälkeen on kaksi mustaa marmoria.

c) Tapahtuman B on hankkia vähintään kaksi mustaa marmoria, määritä tämän tapahtuman tulosjoukot B.

d) Mikä on todennäköisyys, että tapahtuma tapahtuu?

e) Löydä todennäköisyys, että tapahtuma B.

f) Määritä todennäköisyys, että satunnaisen kokeen tulos on, että ainakin yksi musta marmori. Tätä tapahtumaa kutsutaan c.

Kuva 2. Musta ja musta marmorit satunnaisiin kokeisiin. Lähde: NeedPix.

Liittää jhk

Näytetilan rakentamiseksi on hyödyllistä tehdä puukaavio, kuten kuvassa 3 esitetty:

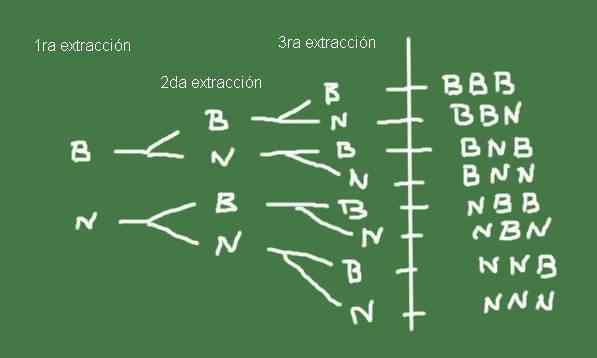Kuva 3. Esimerkiksi puikaavio 2. Valmistettu Fanny Zapata.

Sarja mahdollisia tuloksia kolmen marmorin purkamisesta laukusta, jolla on sama määrä mustia ja mustia marmoreja, on juuri tämän satunnaisen kokeen näytetila.

Ω = (b, b, b), (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n) , (n, n, b), (n, n, n)

Ratkaisu b

Mahdollisia tuloksia, jotka vastaavat tapahtumaa A, joka koostuu kahdesta mustasta marmorista, on:

Voi palvella sinua: Riemannin summa: historia, kaavat ja ominaisuudet, harjoitukset

A = (b, n, n), (n, b, n), (n, n, b)

Liuos C

Tapahtuma B määritellään seuraavasti: "Jos sinulla on ainakin kaksi mustaa marmoria sen jälkeen, kun se on tehnyt kolmen satunnaisen uuttamisen". Mahdolliset tulokset tapahtuman B on:

B = (b, n, n), (n, b, n), (n, n, b), (n, n, n)

Liuos D

Tapahtuman A todennäköisyys on tämän tapahtuman mahdollisten tulosten lukumäärän ja mahdollisten tulosten kokonaismäärä, ts.

P (a) = n (a) / n (ω) = 3/8 = 0.375 = 37.5%

Joten on 37.5%: n todennäköisyys, että kaksi mustaa marmoria on satunnaisesti purettu kolme marmoria laukusta. Mutta huomaa, että emme missään tapauksessa voi ennustaa kokeen tarkan tulosten.

Ratkaisu E

Todennäköisyys, että tapahtuma B on, koostuu ainakin yhdestä mustasta marmorista: on:

P (b) = n (b) / n (ω) = 4/8 = 0.5 = 50%

Tämä tarkoittaa, että tapahtuman Bmahdollisuus on yhtä suuri kuin todennäköisyys, jota ei tapahdu. 

Liuos f

Ainakin yhden mustan marmorin hankkimisen todennäköisyys, että ne on poistettu kolmesta, on yhtä kuin 1 vähemmän todennäköisyys, että tulos on "kolme valkoista marmoria".

P (c) = 1 - p (b b b) = 1 - ⅛ = ⅞ = 0.875 = 87.5%

Nyt voimme tarkistaa tämän tuloksen huomauttaen, että tapahtuman C ollessa C -mahdollisuuksien lukumäärä on yhtä suuri kuin tapahtuman C mahdollisten tulosten lukumäärä:

C = (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n), (n, n, b) , (n, n, n)

N (c) = 7

P (c) = n (c) / n (ω) = ⅞ = 87.5%

Viitteet

1. Canalphi. Satunnainen kokeilu. Palautettu: YouTube.com.
2. Matematiikka. Satunnainen kokeilu. Palautettu: YouTube.com
3. Pishro Nick H . Johdanto todennäköisyyteen. Haettu: Todennäköisyyskuvaa.com
4. Ross. Insinöörien todennäköisyys ja tilastot. MC-Graw Hill.
5. Wikipedia. Koe (todennäköisyysteoria). Haettu: vuonna.Wikipedia.com
6. Wikipedia. Deterministinen tapahtuma. Palautettu: on. Wikipedia.com
7. Wikipedia. Satunnainen kokeilu. Palautettu: on.Wikipedia.com