Jatkuvuusyhtälö

Selitämme, mikä on jatkuvuusyhtälö, sen kaava, sovellukset, esimerkit ja ehdotetaan ratkaistavana harjoituksia

Mikä on jatkuvuusyhtälö?

Se jatkuvuusyhtälö, Puristamattoman nesteen osalta se osoittaa, että putken läpi kiertävän nesteen kokonaismassa on edelleen vakio. Toisin sanoen taikina säilytetään ilman muutoksia, kun nesteen liikkeet.

Puristamaton neste on se, jonka tiheys pysyy suunnilleen vakiona virtaaessa. Esimerkiksi vesi on nestettä, jota pidetään puristamattomana tavanomaisissa paine- ja lämpötila -olosuhteissa.

Jatkuvuusyhtälössä on matemaattinen tapa ilmaista massan säilyttäminen: Annetaan:

-Lla₁∙ V₁ = A₂∙ V₂

Missä v₁ ja v₂ Ne edustavat nesteen nopeutta putken kahdessa osassa₁ jo₂ Ne ovat vastaavat ristikkäiset alueet.

Risti -liitännäisen alueen tuotetta nopeudella kutsutaan virtaus Ja jatkuvuusyhtälö viittaa siihen, että koko putkessa virtaus on vakio. Virtaus tunnetaan myös nimellä tilavuuden virtausnopeus, Se ymmärretään tarkkailemalla huolellisesti edellinen lauseke, jonka mitat ovat tilavuusyksikköä kohti.

Kaava

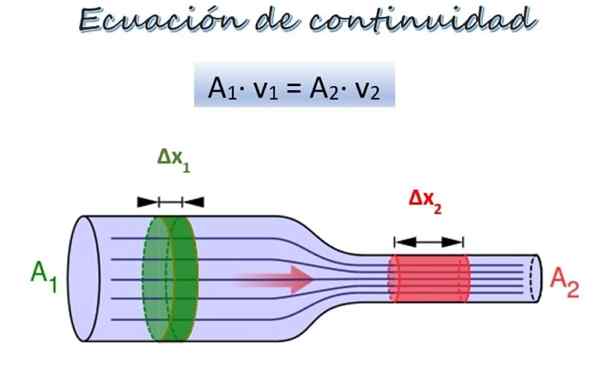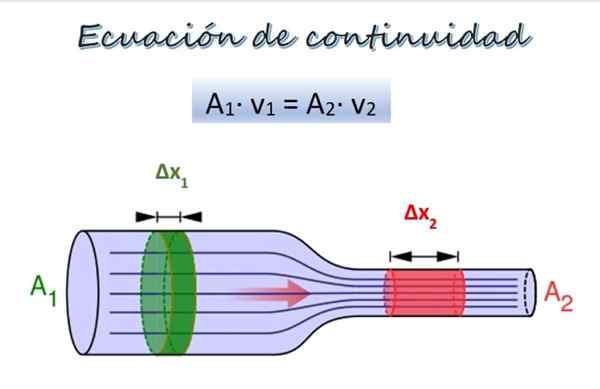
Jatkuvuusyhtälö nesteen virtaukselle eri halkaisijan putkea pitkin. Lähde: Wikimedia Commons/F. Zapata.

Yläkuvassa on putki, jolla on kaksi eri halkaisijan osaa ja samalla korkeudella, vaikka ne voivat olla eri korkeuksilla edustamatta ongelmaa.

Kohdassa 1, leveämpi, ristien alue on₁ ja neste liikkuu nopeudella v₁, Kohdassa 2, kapeampi, risti -aukko on₂ ja nesteen nopeus on v₂.

Taikinan osa ΔM₁ (vihreä) liikkuu jaksolla 1 kerrallaan Δt. Tänä aikana osuus ΔM₂ (Punainen) kulkea jakson 2 läpi. Koska neste on puristamaton, sen tiheys on sama kaikissa pisteissään, joten tiheyden määritelmästä alkaen:

Se voi palvella sinua: Gase Constant: Mikä on, laskenta ja esimerkit

Tässä ρ on tiheys, m on massa ja V -tilavuus. Tämän mukaan massa ΔM₁ on yhtä suuri kuin:

ΔM₁ = ρ ∙ v₁

Missä osa V₁ Se on poikkileikkauksen ja etäisyyden ΔX välinen tuote₁-

ΔM₁ = ρ ∙ (a₁ ∙ Δx₁-A

Mutta sen jälkeen:

Sitten taikinan osa ΔM₁ Voit kirjoittaa nopeuden ja ajan suhteen ΔT: n:

ΔM₁ = ρ ∙ a₁ ∙ Δx₁ = ρ ∙ a₁ ∙ (v₁ ∙ Δt)

Analogi Osa ΔM kirjoitetaan₂ Se virtaa samaan aikaan jaksolla 2:

ΔM₂ = ρ ∙ a₂ ∙ Δx₂ = ρ ∙ a₂ ∙ (v₂ ∙ Δt)

Massan säilyttämällä:

ΔM₁ = ΔM₂

JA:

ρ ∙ a₁ ∙ V₁ ∙ Δt = ρ ∙ a₂ ∙ V₂ ∙ Δt

Kuten Δt ja ρ peruutetaan, tulokset:

-Lla₁ ∙ V₁ = A₂ ∙ V₂

Virtaus q

Poikkileikkauksen A tuotetta nesteen V: n nopeudella kutsutaan virtaukseksi ja se tarkoittaa kuin Q. Se vastaa nesteen tilavuutta putken läpi tai tilavuusvirtausnopeutta: tilavuusvirta:

 V tilavuus ja Δt aikaväli. Kansainvälisen yksikköjärjestelmän virtausnopeus on M³/s, vaikka kuutiometriä, gallonaa/min, gallonat/s litrat/s ja gallonat/s ovat usein. Jotkut eniten käytetyistä muuntotekijöistä ovat seuraavat:

• 1 m³/S = 264.172 gal/s
• 1 l/s = 0.001 m³/s
• 1 jalkaa³/S = 0.0283168 m³/s
• 1 l/s = 0,264172 gal/s
• 1 m³/S = 15850,3 gal/min

Huomaa, että vähentämällä putken poikkileikkausta nesteen nopeus kasvaa ja päinvastoin, jos poikkileikkaus kasvaa, nopeus pienenee siten, että virtaus on vakio.

Sovellukset ja esimerkit

Jatkuvuusyhtälöä käytetään nestevirtauksen analysoinnissa yhdessä Bernoulli -yhtälön kanssa, jossa otetaan huomioon nesteen nopeuden vaihtelut eri osissa, samoin kuin paineen muutokset ja korkeuden vaikutus.

Voi palvella sinua: Suoravirta

Esimerkki 1

Perhepuutarhaletkussa, kun vesi yleensä poistuu suihkusta, on tietty alue, mutta jos se asettaa sormensa letkun poistumiseen, vähentäen lähtöreiää, suihkun alue on suurempi.

Tässä jatkuvuusyhtälö täyttyy, koska vähentämällä lähtösuuttimen pinta -alaa suihkun nopeus kasvaa siten, että nopeuspinta -ala on vakio.

Esimerkki 2

Vesisuihku kapenee sen putoamisen jälkeen, koska sen nopeus kasvaa. Tällä tavoin tuotteen nopeus aluetta kohti pysyy vakiona

Toinen esimerkki, jossa jatkuvuusyhtälö korostetaan.

Tällä tavoin virtaus on vakio, kun taas suihkukone virtaa edelleen laminaarisessa tilassa, ts. Vesi putoaa varovasti ilman turbulenssia tai pyörteitä.

Ratkaisut

Harjoitus 1

Vesi kiertää halkaisijaltaan 20 cm: n putken läpi. Tietäen, että virtaus on 2000 l/s, löydä putkesta veden nopeus.

• Ratkaisu

On kätevää ilmaista kaikki kansainvälisen järjestelmän yksiköissä. Ensinnäkin putken ristikkäinen osa lasketaan, muistaen, että säde on puolet halkaisijasta:

A = π ∙ (d/2)²

D = 20 cm = 0.2 m

Siksi alue on:

A = π ∙ (d/2)² = A = π ∙ (0.2 m /2)² = 0.0314 m².

Virtaus ilmaistaan ​​m³/s asianmukaisen muuntokertoimen avulla:

Q = 2000 l/s = 2 m³/s

Kaavasta Q = A ∙ V nopeus, jolla neste kiertää putken läpi, puhdistetaan:

Harjoitus 2

Sinulla on muuttuva ristikkäinen putki, jonka läpi vesi virtaa. Tietyssä vaiheessa poikkileikkaus on 0.070 m² Ja veden nopeus on 3.50 m/s. Laskea:

Voi palvella sinua: Pascal -periaate: historia, sovellukset, esimerkit

a) Veden nopeus putken toisessa pisteessä, jonka poikkileikkausalue on 0.105 m².

b) Veden tilavuus, joka purkautuu avoimella päällä 1 tunnissa.

• Liittää jhk

Käytetään jatkuvuusyhtälöä, mikä vastaa ensimmäisen pisteen virtausta toisen virtauksen kanssa. Virtaus on:

Q = a ∙ v

Jatkuvuutta varten:

Q -₁ = Q₂

-Lla₁ ∙ V₁ = A₂ ∙ V₂

Nyt he korvaavat lausunnon toimittamat tiedot:

• -Lla₁ = 0.070 m²
• v₁ = 3.50 m/s
• -Lla₂ = 0.105 m²
• v₂ =?

Ja puhdistaa v₂-

Ratkaisu b

Koska virtaus on myös tilavuusaika, sen on:

Siksi volyymi V on:

V = q ∙ Δt = (a ∙ v) Δt

Virtaus, joka voidaan laskea pisteen 1 tai pisteen 2 tiedoilla, koska se on sama molemmissa kohdissa:

Q = a₁ ∙ V₁ = 0.070 m² ∙ 3.50 m/s = 0.245 m³ / s

Tietäen, että 1 tunti = 3600 s, veden tilavuus on:

V = q ∙ Δt = (0.245 m³ / s) × (3600 s) = 882 m³

1 tunnissa 882 m ladataan³ vettä putken läpi.