Tavallinen arviointivirhe Kuinka laskettu, esimerkit, harjoitukset

Hän Vakioarviointivirhe Mittaa poikkeama näytteen populaation arvossa. Eli tavanomainen arviointivirhe mittaa näytteen keskiarvon mahdolliset variaatiot suhteessa väestön keskiarvon todelliseen arvoon.

Esimerkiksi, jos haluat tietää maan (väestön keskiarvo) keskimääräinen ikä, otetaan pieni ryhmä asukkaita, jota kutsumme "näyttelyiksi". Siitä poistetaan keskimääräinen ikä (näytteen keskiarvo) ja oletetaan, että populaatiolla on kyseinen keski -ikä vakioarviointivirhe, joka vaihtelee enemmän tai vähemmän.

M. W -. Toews [CC 2: lla.5 (https: // creativecommons.Org/lisenssit/by/2.5)]

On huomattava, että on tärkeää olla sekoittamatta vakiopoikkeamaa vakiovirheeseen ja standardiestimointia:

1- Vakiopoikkeama on datan dispersion mitta; eli se on populaation vaihtelun mitta.

2- Vakiovirhe on näytteen vaihtelun mitta, joka on laskettu populaation keskihajonnan perusteella.

3- Vakioarviointivirhe on virheen mitta, joka tehdään otoksen keskiarvon ollessa arviona väestön keskiarvosta.

[TOC]

Kuinka se lasketaan?

Vakioarviointivirhe voidaan laskea kaikille näytteistä saatuille mittauksille (esimerkiksi keskimääräinen keskimääräinen arviointi- tai vakiovirhe keskihajonnan arvioinnista) ja mittaa virheen, joka tehdään arvioitaessa todellista populaation mittausta sen näytteen arvosta

Vakioestimointivirheestä vastaavan toimenpiteen luottamusväli rakennetaan.

Voi palvella sinua: Käänteinen matriisi: Laskenta ja liikunta ratkaistu

Vakioarviovirheen kaavan yleinen rakenne on seuraava:

Vakioarviointivirhe = ± luottamuskerroin * Vakiovirhe

Luottamuskerroin = Näytteen tilasto- tai näytteenottojakauman raja.

Vakiovirhe = populaation keskihajonta jaettuna näytteen koon neliöjuurella.

Luottamuskerroin osoittaa vakiovirheiden määrän, jotka ovat valmiita lisäämään ja vähentämään räätälöityjä tiettyyn luottamustasoon tuloksiin.

Esimerkkejä laskelmasta

Oletetaan.

Otetaan N -ihmisistä ja näytteen osuus P ja sen komplementti Q määritetään.

Vakioarviointivirhe (EEE) = ± luottamuskerroin * Vakiovirhe

Luottamuskerroin = z = 1.96.

Vakiovirhe = näytteen osuuden tuotteen neliöjuuri sen komplementin ja näytteen n koon välillä.

Tavallisen arvioiden virheen mukaan aikaväli, jossa väestöpopulaatio tai näytteen osuus muista näytteistä, jotka voidaan muodostaa kyseisestä populaatiosta, on 95%: n luotettavuustaso:

P -EEE ≤ populaation osuus ≤ p + eee

Ratkaisut

Harjoitus 1

1- Oletetaan, että yrität arvioida väestössä olevien ihmisten osuutta, jotka pitävät mieluummin rikastettua meijerikaavaa, ja haluat 95%: n luottamusta tuloksiinsa.

Voi palvella sinua: synteettinen jako

Otetaan 800 ihmistä, ja on määritetty, että otoksen 560 ihmistä on mieluummin rikastettua maitotuotteita. Määritä aikaväli, jossa väestön osuus voidaan odottaa, ja muiden näytteiden osuus, jotka voidaan ottaa väestöstä, 95%: n luottamuksella

A) Lasketaan näytteen osuus p ja sen komplementti:

P = 560/800 = 0.70

Q = 1 -p = 1 -0.70 = 0.30

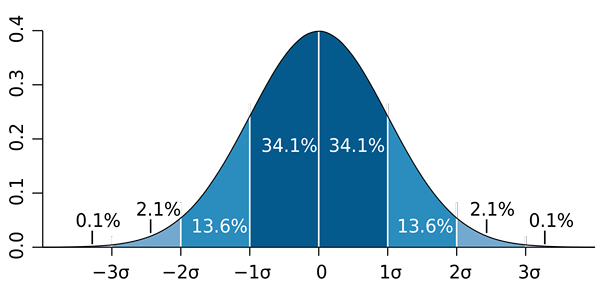
b) Tiedetään, että osuus lähestyy normaalia jakautumista suurikokoisiin näytteisiin (yli 30). Sitten sovelletaan niin kutsuttuja sääntöä 68 - 95 - 99.7 Ja sinun täytyy:

Luottamuskerroin = z = 1.96

Vakiovirhe = √ (p*q/n)

Vakioestimointivirhe (EEE) = ± (1.96)*√ (0.70)*(0.30)/800) = ± 0.0318

c) Vakioarviointivirheestä, jonka väestön osuus odotetaan 95%: n luottamustasolla:

0 -.70 -0.0318 ≤ populaation osuus ≤ 0.70 + 0.0318

0 -.6682 ≤ populaation osuus ≤ 0.7318

Voit odottaa, että 70%: n näytteen osuus muuttuu 3: een.18 prosenttiyksikköä, jos se vie erilaisen 800 yksilön otoksen tai että väestön todellinen osuus on välillä 70 - 3.18 = 66.82% ja 70 + 3.18 = 73.18%.

Harjoitus 2

2- Otamme Spiegelin ja Stephens, 2008, seuraava tapaustutkimus:

Yliopiston ensimmäisen vuoden opiskelijoiden matematiikan kokonaisluokista otettiin satunnainen otos 50 pätevyydestä, jossa havaittu keskiarvo oli 75 pistettä ja keskihajonta, 10 pistettä. Mitkä ovat 95%: n luottamusrajat yliopiston matematiikan pätevyyden keskiarvon arvioinnille?

Se voi palvella sinua: mikä on Rhombus -alueen ja suorakulmion välinen suhde?

A) Lasketaan tavanomainen arviointivirhe:

95%: n luottamuskerroin = z = 1.96

Vakiovirhe = s/√n

Vakioestimointivirhe (EEE) = ± (1.96)*(10√50) = ± 2.7718

b) Vakioiden arviointivirheestä, jonka väestö keskiarvo tai toisen näytteen keskiarvo on 50, luotettavuustaso on 95%:

50 -2.7718 ≤ väestön keskiarvo ≤ 50 + 2.7718

47.2282 ≤ väestön keskiarvo ≤ 52.7718

c) Voit odottaa, että näytteen keskiarvo muuttuu jopa 2.7718 pistettä, jos otetaan erilainen otos 50 luokasta tai että yliopiston väestön matematiikan luokkien todellinen keskiarvo on välillä 47.2282 pistettä ja 52.7718 pistettä.

Viitteet

1. Abraira, V. (2002). Vakiopoikkeama ja vakiovirhe. Semergen -aikakauslehti. Verkko palautettu.Arkisto.org.
2. Rumsey, D. (2007). Keskitilastot nukkeille. Wiley Publishing, Inc.
3. Salinas, H. (2010). Tilastot ja todennäköisyydet. Matosta toipuminen.Uda.Cl.
4. Sokal, r.; Rohlf, f. (2000). Biometria. Biologisen tutkimuksen tilastojen periaatteet ja käytäntö. Kolmas Ed. Blume -versiot.
5. Spiegel, M.; Stephens, L. (2008). Tilastot. Neljäs Ed. McGraw-Hill/Amerikanvälinen Meksikosta. -Lla.
6. Wikipedia. (2019). 68-95-99.7 sääntö. Haettu jstk.Wikipedia.org.
7. Wikipedia. (2019). Vakiovirhe. Haettu jstk.Wikipedia.org.