Fraktiotyypit, esimerkit, harjoitukset ratkaistu

Se fraktiot jompikumpi murtoluku Ne ovat niitä lukuja, jotka ovat edustettuna osoittaen kahden kokonaisluvun välisen osamäärän -lla ja b -, niin kauan kuin b - on erilainen kuin 0. Esimerkiksi 1/3 on murto -osa, joka lukee nimellä "kolmasosa".

Lukuun ottamatta -lla Se tunnetaan nimellä osoittaja ja murto- ja b - kuten nimittäjä Samasta. Nimittäjä osoittaa, kuinka monta osaa koko on jaettava. Osoitin puolestaan ​​osoittaa kuinka monta osaa koko tuosta.

Kuvio 1. Kuinka monta osaa tällä suklaapalkissa on? Lähde: Piqsels.

Koko on mikä tahansa, joka haluaa jakaa tai murto -osan, esimerkiksi pizza tai kuvassa 1 esitetty suklaapalkki. Pylväs on tehty siten, että se on erittäin helppo jakaa viiteen yhtä suureen osaan, missä kukin osa on 1/5 koko palkista.

Jakeessa tai murto -osassa numeroa 1/5, osoitin on 1 arvoinen ja nimittäjän arvoinen 5. Jakelu on "viidesosa".

Oletetaan, että syömme 3 kappaletta suklaata. Sanoisimme, että olemme syöneet 3/5 osaa baarista ja 2/5 osaa on jätetty jakamaan ystävän kanssa. Voimme myös sanoa, että söimme "kolme viidennen suklaata" ja annamme ystävälle "kaksi viidesosaa".

Näiden murto -lukujen graafinen esitys on seuraava:

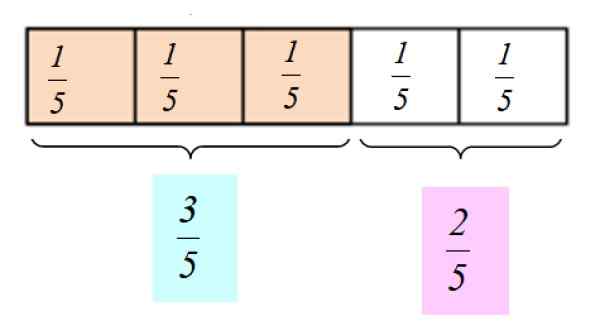Kuva 2.- Fraktioiden graafinen esitys 3/5 ja 2/5. Lähde: f. Zapata.

[TOC]

Fraktiotyypit

Omat fraktiot

Murto on oma, kun osoittaja on pienempi kuin nimittäjä ja siten sen arvo on alle 1. Edellisen osan fraktiot, suklaan esimerkissä, ovat heidän omat fraktiot.

Muita esimerkkejä omasta fraktiostaan ​​ovat: ½; 8/10; 3/4 ja enemmän.

Kuva 3.- Sekä 1/4 että 1/2 ovat heidän omat fraktiot. Lähde: Wikimedia Commons.

Virheelliset fraktiot

Väärin fraktioiden osoittaja on suurempi kuin osoittaja. Esimerkiksi 4/3, 8/5, 21/10 kuuluvat tähän luokkaan.

Näennäiset fraktiot

Nämä fraktiot edustavat koko numeroa. Heidän joukossaan on 4/2, 10/5 ja 27/3, koska jos näytämme hyvältä, näiden fraktioiden nimittäjän jakamisen tulos antaa kokonaislukuluvun.

Siten: 4/2 = 2, 10/5 = 2 ja 27/3 = 9.

Vastaavat fraktiot

Kaksi fraktiota N/M ja P/Q ovat vastaavia, kun jakautuu nimittäjän välillä, sama määrä saadaan. Tällä tavoin vastaavat fraktiot edustavat samaa osaa kokonaisuudesta.

Esimerkiksi meillä on fraktioita: 15/2 ja 30/4. Jaettamalla 15: llä saat 7.5, mutta se on myös sama, jos 30 on jaettu 4: llä.

Voi palvella sinua: injektiotoiminto: mistä se koostuu, mihin se on ja esimerkkejä

Tietää, onko kaksi fraktiota N/M ja P/Q vastaavia, seuraavan tasa -arvon noudattaminen todennetaan:

N*q = m.p

Peruuttamattomat fraktiot

Kun numeraattori ja nimittäjä jaetaan sekä samalla kuvalla että niin kauan kuin tulos on kokonainen, saadaan murto -osa, mutta pienemmillä numeroilla.

Tämä prosessi jatkuu, kun osoittajalla ja nimittäjällä on sama tarkka jakaja. Kun ei ole mahdollista jatkaa jakamista on, että Peruuttamaton osuus alkuperäisen osan.

Etu, joka on työskenneltävä peruuttamattoman fraktion kanssa, on, että saadaan vastaava osa, mutta pienemmillä numeroilla. Siksi kun työskentelet fraktioiden kanssa, sinun on varmistettava, että vähentävät niitä aina kun mahdollista, laskelmien helpottamiseksi.

Oletetaan, että osuus 12/20 on osoitus- ja nimittäjäparia, molemmat voidaan jakaa 2: n:

12/20 = 6/10

Ja vielä kerran:

6/10 = 3/5

3/5 -osa vastaa 12/20, mutta yksinkertaisempaa.

Sekarakennukset

Väärä fraktio myöntää myös edustuksen sekoitettuna lukumääränä, jota kutsutaan niin, koska sillä on koko osa ja toinen murto -osa, murto -osa on omaa murto -osaa.

Katsotaanpa nopeaa esimerkkiä, jossa on murto -osan 15/2, jonka tiedämme vastaavat 7.5.

Voimme ilmaista 15/2: een tällaisena sekoitettuna numerona:

15/2 = 7 + 0.5

Mutta 0.5 = ½. Siksi 15/2 = 7½, joka lukee "Seitsemän ja keskipitkän".

Esimerkkejä fraktioista

Jakeluvut ovat välttämättömiä, koska sekä luonnolliset että kokonaisluvut ovat riittämättömiä, kun haluamme jakaa esimerkiksi suklaapalkin.

Ja siksi on ääretön monenlaisia ​​mittausmalleja ja esineitä, joiden vaatimukset sisältävät murto -luvut, puhumattakaan päivittäisten tilanteiden määrästä, joissa nämä ovat välttämättömiä.

Ruokaostot

Maissa, joissa desimaalimetristä järjestelmää käytetään, kilon käyttö on yleinen viitaten monien elintarvikkeiden painoon. Emme aina halua ostaa kokonaisia ​​määriä, mutta vähän enemmän tai vähän vähemmän.

Siksi kysymme:

• ½ kg kalaa
• ¾ kg tomaattia
• ¼ kilo sipulia
• 1 ½ kg persikoita (1 ja puoli kilo).

Ja kun käytetään anglo -takson mittauskuvioita, sama tapahtuu: tarvitsemme 2 ja puoli kiloa tai 1/4 jotain jotain.

Voi palvella sinua: toimintojen arviointi

Kaikki nämä numerot ovat murto -osia, ja kuten olemme nähneet, ne vastaavat kahta erityyppistä fraktiota: omat ja väärät.

Keittiön reseptit

Keittiön reseptit käyttävät usein murto -lukuja tiettyjen ainesosien lukumäärän osoittamiseksi. Esimerkiksi:

• ½ kuppi jauhoja
• ¾ kg sokeria kakun valmistamiseksi.

Pituudet ja halkaisijat

Huonekalujen mitat, tekstiilit ja kaikenlaiset kotimaiset välineet mitataan metro- tai tuuman fraktioissa riippumatta.

Jopa maissa, joissa desimaalimetrinen järjestelmä vallitsee, kaupallinen kupari, teräs ja muut putkityömateriaalit toimitetaan yleensä tuuman halkaisijoilla. Samoin muut laitteistot, kuten ruuvit ja mutterit.

Tuumana vastaa 2.54 cm, yleensä nämä kappaleet, joilla on pienet halkaisijat, ilmaistaan ​​tuuman jakeluina.

Erittäin yleiset kotimaisten putkien toimenpiteet ovat:

• ½ tuumaa
• ¼ tuumaa
• 3/8 ja 5/8 tuumaa.

Aikarajat

Päivittäin murto -lukuja käytetään ilmaisemaan aikavälejä, kuten ¼, ½ ja ¾ tunnin tai jopa hiukan suurempia: 1 tunti ja ¼ ja niin edelleen.

Kuva 4. He ovat puolet yksitoista tämän käden kellolla. Lähde: Pixabay.

Harjoitukset fraktioilla

- Harjoitus 1

Nykyään Juanito on ottanut kakun syntymäpäiväänsä kouluun ja haluaa jakaa sen kaikkien ystäviensä keskuudessa, mutta opettaja haluaa antaa kappaleen, joka on kolme kertaa suurempi lasten suhteen.

Ottaen huomioon, että opettajaa on 24 lasta +, jolle hän haluaa antaa vastaavan kolme kappaletta, kuinka monta kappaletta kakun tulisi leikata?

Ratkaisu

Jos Juanito halusi jakaa kakun vain ystäviensä keskuudessa, jokainen vastaa 1/24.

Mutta koska opettaja haluaa antaa osan ja. Eli kukin lapsi vastaa 1/27 kappaletta ja opettaja 3/27 kappaletta.

Lisäksi, jos vähentämme 3/27 -fraktiota, saamme opettajan ottamaan 1/9 osaa kakusta.

- Harjoitus 2

Yrityksellä, jolla on pomo ja kolme työntekijää, on 6000 euroa tuloja joka kuukausi. Kuinka paljon rahaa kukin henkilö vastaa, jos pomo haluaa pitää puolet siitä, mitä hän voitti?

Voi palvella sinua: Rhomboid: Ominaisuudet, kuinka kehä ja alue vie pois

Ratkaisu

Jos pomo haluaa voittaa puolen, hänen on pysyttävä 6000/2, mikä tekee 3000 euroa. Muista jäljellä olevista 3000 eurosta on se, mitä kolme työntekijää tulisi jakaa. Siten jokainen työntekijä voittaa 3000/3, mikä johtaa 1000 euroa.

- Harjoitus 3

Löydä peruuttamaton osa:

a) 12/18 ja b) 4/11

Liittää jhk

Ensimmäisessä tapauksessa huomasimme, että sekä numeroija että nimittäjä ovat tasaisia ​​ja jaettavissa 2: n välillä. Ne ovat myös jaettavissa 3: n välillä, koska 12 ja 18 ovat monikerroksia siitä.

Joten voimme yksinkertaistaa fraktiota jakamalla sekä numeroija että nimittäjä joko 2 tai 3 välillä, järjestys on välinpitämätön.

Alkaen jakamisesta 2:

12/18 = 6/9

Nyt huomataan, että sekä tämän vastaavan fraktion nimeäjä että nimittäjä ovat 3: n kertoimia, joten jakavat molemmat tämän luvun välillä:

6/9 = 2/3

Ja koska 2 ja 3 ovat ensisijaisia ​​lukuja, heillä ei enää ole muuta yleistä jakajaa paitsi 1. Olemme saavuttaneet peruuttamattoman osan.

Suurin osakumppanin ja nimittäjän suurin yhteinen MCD -jakaja olisi voitu laskea. 12 ja 18:

MCD (12,18) = 6.

Ja sitten numeroija ja nimittäjä on jaettu tällä numerolla, mikä vastaa niin vaiheita.

Ratkaisu b

Tässä havaitsemme, että 11 on ensisijainen luku ja sen jakajat ovat 1 ja 11. Puolestaan ​​4 myöntää jakautuneina 4, 2 ja 1. Lukuun ottamatta 1, näillä numeroilla ei ole yhteistä jakajaa, ja siksi 4/11 -osa on peruuttamaton.

- Harjoitus 4

Ilmoita mikä on jokaisen parin suurin osa:

a) ¾ ja 5/4

b) 3/7 ja 4/9

Liittää jhk

Kun kahdella positiivisella fraktiolla on sama nimittäjä, suurin on yksi, jolla on suurin osoittaja. Siksi 5/4 on suurempi, koska 5> 3.

Ratkaisu b

Jos fraktiot N/M ja P/Q on erilainen nimittäjä ja molemmat ovat positiivisia, vertailukriteerit ovat seuraavat:

Ilman.Q> m. P, sitten n/m> p/q

Toinen vaihtoehto on löytää kunkin fraktion desimaalin ilmaisu ja verrata.

Ensimmäisen kriteerin mukaan: n = 3, m = 7, p = 4, q = 9. Siksi: n.Q = 3*4 = 12 ja m.P = 7*4 = 28.

Kuten 12< 28, ocurre que 3/7 < 4/9.

Tai ilmaisemme jokaisen fraktion desimaalina, hankkimalla tämän:

3/7 = 0.428571428… .

4/9 = 0.44444444… .

Suspensat osoittavat, että desimaalien määrä on ääretön. Mutta tämä riittää varmistamaan, että todellakin 4/9> 3/7.

Viitteet

1. Baldor, a. 1986. Aritmeettinen. Codex -versiot ja jakaumat.
2. Carena, m. 2019. Matematiikan käsikirja. Rannikon kansallinen yliopisto.
3. Figuera, J. 2000. Matematiikka 8. Co-bo-painikkeet.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Matematiikan sivu. Mikä on murto -osa? Toipunut: ThemathPage.com.