Absoluuttinen taajuuskaava, laskenta, jakauma, esimerkki

Se Absoluuttinen freekuusia Se määritellään kuinka monta kertaa samat tiedot toistetaan numeerisen muuttujan havaintojen sisällä. Kaikkien absoluuttisten taajuuksien summa vastaa tietojen kokonaismäärää.

Kun tilastollisesta muuttujasta on monia arvoja, on kätevää organisoida ne oikein, jotta saadaan tietoa heidän käyttäytymistään. Tällaiset tiedot annetaan keskeisillä taipumustoimenpiteillä ja dispersiotoimenpiteillä.

Kuvio 1. Tilastollisen havainnon absoluuttinen taajuus on avain tietojoukkoa seuraavan trendin löytämiseen

Näiden toimenpiteiden laskelmissa tiedot esitetään sen taajuuden kautta, jolla ne ilmestyvät kaikissa havainnoissa.

Seuraava esimerkki osoittaa, kuinka kunkin datan absoluuttisen taajuuden paljastaminen on. Toukokuun ensimmäisellä puoliskolla nämä olivat parhaiden jakamisen cocktail -pukujen koot, hyvin tunnettujen naisten vaatevarasto:

8; 10; 8; 4; 6; 10; 12; 14; 12; 16; 8; 10; 10; 12; 6; 6; 4; 8; 12; 12; 14; 16; 18; 12; 14; 6; 4; 10; 10; 18

Kuinka monta mekkoa myydään tietyssä koossa, esimerkiksi koko 10? Omistajat ovat kiinnostuneita tietämään tilauksia.

Tietojen tilaaminen on helpompaa laskea, yhteensä on tarkalleen 30 havaintoa kuin pienimmästä korkeimpaan on tällainen:

4; 4; 4; 6; 6; 6; 6; 8; 8; 8; 8; 10; 10; 10; 10; 10; 10; 12; 12; 12; 12; 12; 12; 14; 14; 14; 16; 16; 18; 18

Ja nyt on selvää, että koko 10 toistetaan 6 kertaa, joten sen absoluuttinen taajuus on yhtä suuri kuin 6. Sama menettely suoritetaan jäljellä olevien koon absoluuttisen taajuuden selvittämiseksi.

[TOC]

Kaavat

Absoluuttinen taajuus, nimeltään f_Yllyttää, Se on yhtä suuri kuin tiettynä x -arvon lukumäärä_Yllyttää on havaintojen ryhmässä.

Olettaen, että kokonaishavainnot ovat N -arvoja, kaikkien absoluuttisten taajuuksien summan on oltava yhtä suuri kuin mainittu luku:

Voi palvella sinua: papruda

∑f_Yllyttää = f₁ + F₂ + F₃ +… F_n = N

Muut taajuudet

Jos jokainen F -arvo_Yllyttää Se on jaettu tietojen kokonaismäärällä n, sinulla on suhteellinen taajuus F_{r -} arvo x_Yllyttää-

F_{r -} = f_Yllyttää / N

Suhteelliset taajuudet ovat arvoja välillä 0 ja 1, koska n on aina suurempi kuin mikään F_Yllyttää, Mutta summan on oltava yhtä suuri kuin 1.

Kertomalla 100: lla jokaiselle F -arvolle_{r -} sinulla on Suhteellinen prosenttiosuus, jonka summa on 100%:

Suhteellinen prosenttiosuus = (f_Yllyttää / N) x 100%

Se on myös tärkeää kertynyt taajuus F_Yllyttää Kunnes tietty havainto, tämä on kaikkien absoluuttisten taajuuksien summa, kunnes mainitut havainnot sisältävät:

F_Yllyttää = f₁ + F₂ + F₃ +… F_Yllyttää

Jos kertynyt taajuus on jaettu datan kokonaismäärällä n, sinulla on kertynyt suhteellinen taajuus, joka kerrotaan 100: ta kohti, johtaa kertynyt suhteellinen taajuusprosentti.

Kuinka saada absoluuttinen taajuus?

Tietyn arvon absoluuttinen taajuus, joka kuuluu tietojoukkoon, ne kaikki on järjestetty vähiten suurimpaan ja arvo lasketaan.

Mekkojen koon esimerkissä koko 4: n absoluuttinen taajuus on 3 mekkoa, eli f₁ = 3. Koko 6: lle myytiin 4 mekkoa: f₂ = 4. Myös kooltaan 8 4 mekkoja myytiin, f₃ = 4 ja niin edelleen.

Taulukko

Kokonaistulokset voidaan esittää taulukossa, joka näyttää kunkin absoluuttiset taajuudet:

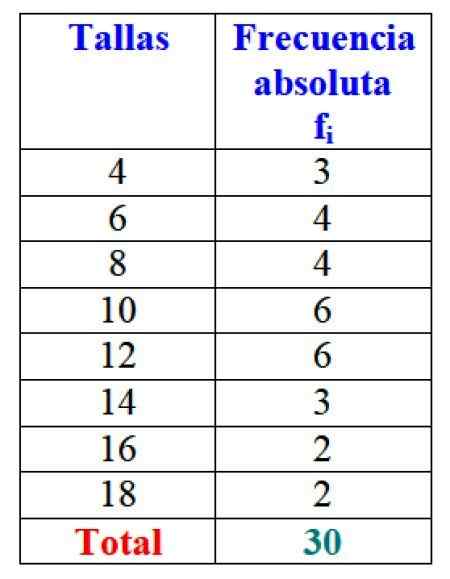Kuva 2. Taulukko, joka edustaa muuttujaa "myyty myynti" ja vastaavat absoluuttiset taajuudet. Lähde: f. Zapata.

On selvää, että on edullista tilata tiedot ja pystyä käyttämään sitä sen sijaan, että työskentelisit löysällä datalla.

Tärkeä: Huomaa, että lisäämällä kaikki sarakkeen F arvot_Yllyttää  Tietojen kokonaismäärä on aina saatu. Jos ei, kirjanpito on tarkistettava, koska virhe on.

Laaja taajuuspöytä

Edellistä taulukkoa voidaan laajentaa lisäämällä muun tyyppisiä taajuutta peräkkäisissä sarakkeissa oikealle:

Voi palvella sinua: Homocedaticity: Mikä on, merkitys ja esimerkit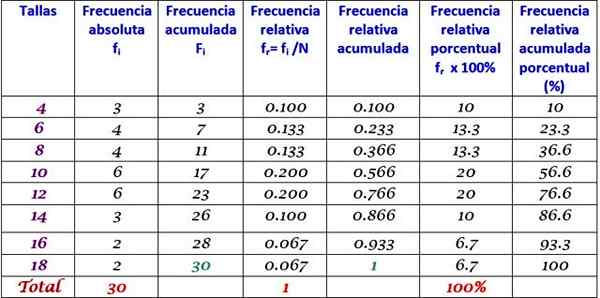

Taajuusjakauma

Taajuusjakauma on seurausta datan järjestämisestä niiden taajuuksien suhteen. Kun työskentelet monien tietojen kanssa, on kätevää ryhmitellä ne luokkiin, väliajoihin tai luokkiin, jokaisella on vastaavat taajuudet: absoluuttiset, suhteelliset, kertyneet ja prosenttiosuus.

Niiden tekemisen tavoitteena on päästä helpommin tietoihin, joita tiedot sisältävät, samoin kuin tulkita niitä oikein, mikä ei ole mahdollista, kun ne esitetään ilman järjestystä.

Kokojen esimerkissä tietoja ei ole ryhmitelty, koska ne eivät ole liian monta kokoa ja niitä voidaan helposti manipuloida ja laskea. Laadullisia muuttujia voidaan myös työskennellä tällä tavalla, mutta kun tietoja on erittäin paljon, ne työskentelevät paremmin ryhmittelemällä ne luokkiin.

Ryhmitetyn datan taajuusjakauma

Tietojen ryhmittymiseksi yhtä suuret luokat seuraavia on otettava huomioon:

-Koko, leveys tai luokan amplitudi: Se on ero luokan suurimman arvon ja alaikäisen välillä.

Luokan koosta päätetään jakamalla alue R: n lukumäärän mukaan. Alue on ero tietojen maksimiarvon ja alaikäisen välillä, kuten tämä:

Luokan koko = alue / luokkien lukumäärä.

-Luokkaraja: aikaväli, joka siirtyy luokan ylärajan alarajasta.

-Luokan tuotemerkki: Se on aikavälin keskipiste, jota pidetään luokan edustavana. Se lasketaan ylärajan ja luokan alarajan puoliksi limien kanssa.

-Luokkien lukumäärä: Sturges -kaavaa voidaan käyttää:

Luokat = 1 + 3 322 log n

Missä n on luokkien lukumäärä. Kuten yleensä desimaaliluku, seuraava on pyöristetty.

Esimerkki

Suuri tehdaskone ei ole toiminnassa, koska sillä on toistuvia vikoja. Mainitun koneen peräkkäiset passiivisuuden ajanjaksot minuutteina on tallennettu alla, yhteensä 100 data:

Se voi palvella sinua: Taajuuden todennäköisyys: Konsepti, miten se lasketaan ja esimerkkejä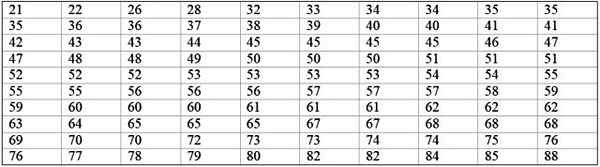

Ensinnäkin luokkien lukumäärä määritetään:

Luokat = 1 + 3,32 log n = 1 + 3.32 log 100 = 7.64 ≈ 8

Luokan koko = luokkien lukumäärä = (88-21) / 8 = 8.375

Se on myös desimaalin lukumäärä, joten se vie 9 luokan kokoa.

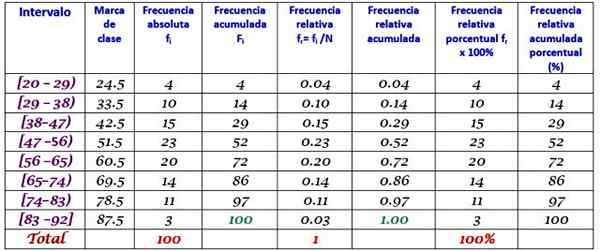
Luokan tuotemerkki on keskiarvo luokan ylä- ja alarajan välillä, esimerkiksi luokan [20-29) välillä on merkki:

Luokkabrändi = (29 + 20) / 2 = 24.5

Jatka samalla tavalla löytääksesi jäljellä olevien väliajojen luokan tuotemerkit.

Liikuntaa

40 nuorta ilmoitti, että seuraavana sunnuntaina Internetissä kuluneissa minuutteissa oli yhä enemmän:

0; 12; kaksikymmentä; 35; 35; 38; 40; Neljä viisi; 45, 45; 59; 55; 58; 65; 65; 70; 72; 90; 95; 100; 100; 110; 110; 110; 120; 125; 125; 130; 130; 130; 150; 160; 170; 175; 180; 185; 190; 195; 200; 220.

Näiden tietojen taajuuden jakauma pyydetään.

Ratkaisu

N = 40 datan sarjan R R on:

R = 220 - 0 = 220

Sturges -kaavan soveltaminen luokkien lukumäärän määrittämiseksi tuottaa seuraavan tuloksen:

Luokat = 1 + 3,32 log n = 1 + 3.32 loki 40 = 6.3

Kuten desimaali, välitön kokonaisuus on 7, siksi tiedot on ryhmitelty 7 luokkaan. Jokaisen luokan leveys on:

Luokan koko = luokkien lukumäärä = 220/7 = 31.4

Sulje ja pyöreä arvo on 35, joten luokan leveys on 35.

Luokkamerkit lasketaan keskiarvoa kunkin aikavälin yläraja ja alaraja, esimerkiksi aikavälille [0,35):

Luokkabrändi = (0+35)/2 = 17.5

Jatkamme samalla tavalla jäljellä olevien luokkien kanssa.

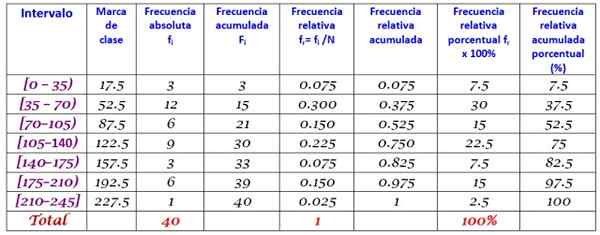
Lopuksi, taajuudet lasketaan yllä kuvatun menettelyn mukaisesti, mikä johtaa seuraavaan jakaumaan:

Viitteet

1. Berenson, m. 1985. Hallinnon ja taloustieteen tilastot. Inter -American S.-Lla.
2. DeVore, J. 2012. Tekniikan ja tieteen todennäköisyys ja tilastot. Kahdeksas. Painos. Kyynärmä.
3. Levin, r. 1988. Järjestelmänvalvojien tilastot. Toinen. Painos. Prentice Hall.
4. Spiegel, M. 2009. Tilastot. Schaum -sarja. 4 ta. Painos. McGraw Hill.
5. Walpole, r. 2007. Tekniikan ja tieteen todennäköisyys ja tilastot. Pearson.