Yleiset kaava neliöyhtälöt, esimerkit, harjoitukset

Se Yleinen kaava, joka tunnetaan myös nimellä liuottimen kaava Joissakin teksteissä sitä käytetään toisen asteen yhtälöiden ratkaisemiseen: kirves² + BX + C = 0.

Heissä -lla, b - ja c Ne ovat todellisia lukuja, sillä ehdolla -lla on erilainen kuin 0, oleminen x Tuntematon. Sitten yleinen kaava esittelee tuntemattoman puhdistuman lausekkeella, joka sisältää arvot -lla, b - ja c seuraavasti:

Kuvio 1. Matematiikan yleistä kaavaa käytetään kvadraattisten yhtälöiden ratkaisemiseen. Lähde: f. Zapata.

Ja tämän kaavan kautta löydät minkä tahansa toisen asteen tai neliömäisen yhtälön ratkaisun, mikäli mainittu ratkaisu on olemassa.

Historioitsijoiden mukaan muinainen Babylonian matematiikka tunnetaan jo yleinen kaava. Myöhemmin se siirrettiin muihin kansoihin, kuten egyptiläisiin ja kreikkalaisiin, kulttuurivaihtojen kautta.

Kaava ja sen variantit saapuivat Eurooppaan muslimimatemaattien ansiosta, jotka asettuivat Iberian niemimaalle. He eivät kuitenkaan käyttäneet algebrallista merkintää, jota tällä hetkellä käytämme. Tämä merkintä johtuu Ranskan matemaatikoista ja 16. vuosisadan salausasiantuntijasta Francois Viette.

[TOC]

Yleisen kaavan neliömäiset yhtälöt

Katsotaanpa kuinka yleinen kaava syntyy sen pätevyyden varmistamiseksi. Alkaen yleisestä kvadraattisesta yhtälöstä:

kirves² + BX + C = 0

Otetaan käytännössä joitain yksinkertaisia ​​algebrallisia manipulaatioita tuntemattoman puhdistuman saavuttamiseksi. Tämän kantamiseen on useita tapoja, esimerkiksi neliöiden suorittaminen, kuten silloin kuvataan.

Yleisen kaavan osoittaminen

Aloitamme lisäämällä (-c) tasa-arvon molemmille puolille:

kirves² + Bx = - c

Ja nyt se kerrotaan 4A: lla, aina tasa -arvon molemmilla puolilla, jotta lausekkeita ei muuta:

Neljäs² x² + 4AB x = - 4ac

Lisäämällä b²-

Neljäs²⋅x² + 4AB⋅x + B² = - 4AC + B²

Tämän tarkoituksena on suorittaa neliöt tasa -arvon vasemmalla puolella, joka sisältää tuntemattoman, tällä tavalla sen puhdistumaa helpotetaan. Täten:

Voi palvella sinua: 8: 8: Mitkä ovat helppoja selityksiä

-Ensimmäinen termi: 4² x² Se on täydellinen 2AX: n neliö

-Viimeinen, joka on B², Se on täydellinen b -neliö.

-Ja keskustermi on 2AX: n ja B: 2⋅2AX⋅B = 4ABX kaksoistuote

Siksi meillä on neliömäinen binomi:

Neljäs²⋅x² + 4AB⋅x + B² = (2AX + B)²

Ja voimme kirjoittaa:

(2AX + B)² = - 4AC + B²

Olemme yhden askeleen päässä tuntemattoman tyhjentämisestä x-

Ja saamme jo yleisen kaavan, jonka tiedämme:

On myös muita tapoja manipuloida kvadraattista yhtälöä ja saada sama tulos.

Esimerkkejä yleisen kaavan käytöstä

Yleisen kaavan soveltamiseksi A-, B- ja C -arvot määritetään huolellisesti ja korvataan kaavassa. Huomaa symboli vähemmän osoitimessa; Tämä osoittaa, että meidän on otettava huomioon kaksi operaatiota koskevaa mahdollisuutta, toinen merkki + ja toinen merkinnällä -.

Neliöyhtälöllä voi olla seuraavat ratkaisut subradikaalin määrän arvon mukaan, joka tunnetaan nimellä syrjivä-

-Kyllä B² - 4AC> 0, neliömäisessä yhtälössä on kaksi todellista ja erilaista ratkaisua.

-Kun b² - 4AC = 0, yhtälöllä on ainutlaatuinen ratkaisu, jonka antaa:

x = -b/2a

-Lopuksi, jos b² - 4AC < 0, la ecuación no tiene soluciones reales, pero sí tiene soluciones complejas.

Katsotaanpa joitain esimerkkejä, joissa yleistä kaavaa käytetään, huomaa, että jos jotain tuntemattoman kertoimista ei näy, ymmärretään, että se on 1 arvoinen. Ja jos riippumaton termi on se, jota ei löydy, se on 0 arvoa.

- Esimerkki 1

Ratkaise seuraavat neliömäiset yhtälöt:

a) 6x² + 11x -10 = 0

b) 3x² -5x -1 = 0

Vastaa

Kirjoitamme kunkin termin kertoimet: A = 6, B = 11, C = -10 ja korvata arvot yleisessä kaavassa:

Voi palvella sinua: verotus

x = (-11 ± 19) /12

Tulos johtaa seuraaviin kahteen todelliseen ratkaisuun:

x₁ = (-11 + 19)/12 = 8/12 = 2/3

x₂ = (-11 -19)/12 = -5/2

Vastaus b

Jälleen kertoimet määritetään: a = 3, b = -5 ja c = -1. Korvaamalla kaava:

Toisin kuin edellisessä tapauksessa, 37: n neliöjuuri ei ole kokonaisluku, mutta voimme myös nostaa nämä kaksi ratkaisua ja jättää juuri tai löytää vastaava desimaalin arvo laskimen avulla:

x₁ = (-5 + √37)/6 ≈ 0.18

x₂ = (-5 - √37)/6 ≈ - 1.85

- Esimerkki 2

Ratkaise toisen asteen yhtälö x² - 4x +13 = 0.

Vastaus

Kuten aina, tunnistamme kertoimien arvot ja korvaamme yleisen kaavan: a = 1, b = - 4, c = 13. Tämä johtaa:

Meillä on negatiivinen juuri, joten tämän yhtälön ratkaisut ovat kompleksisia lukuja. Juuri voidaan ilmaista Yllyttää, se Kuvitteellinen yksikkö-

√ (36i²) = 6i

Koska minä² = -1, siksi monimutkaiset ratkaisut ovat:

x₁ = (4 + 6i)/2 = 2 + 3i

x₂ = (4 - 6i)/2 = 2 - 3i

Liikuntaa

10 m pitkä portaikko lepää pystysuuntaista seinää vasten, jalka 6 m siitä seinästä. Portaikko liukuu ja jalka erotetaan 3 m enemmän pohjasta.

Etsi portaikon yläosan läpi kulkeva pystysuora etäisyys.

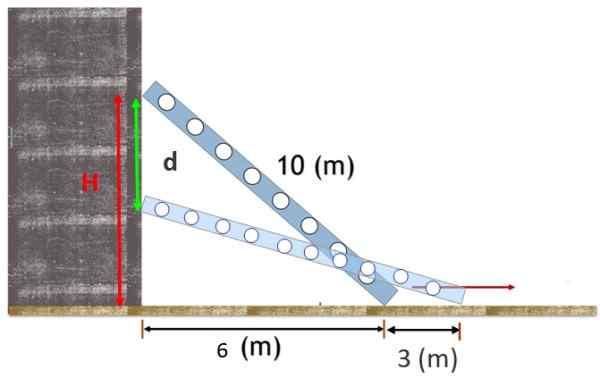Kuva 2. Seinällä tuettu portaikko liukuu hiukan ja yläpysäkki liikkuu pystysuunnassa etäisyydellä D. Lähde: f. Zapata.

Ratkaisu

Portaikon yläosan liukumisen pystysuuntaisen etäisyyden löytämiseksi sinun on löydettävä sijainti, jossa se alun perin koski maata. Voimme tehdä sen Pythagoras -lauseen kanssa, koska muodostettu luku on oikean kolmion kuva:

H = (10² - 6²-A ^½ = 8 m

Kun portaikko liukastuu, etäisyys liikkuu d -d, Mittaa, koska yläosa oli 8 m korkea, kunnes se saavutti uuden aseman, (H-D) metrissä maanpinnan yläpuolella. Selvyyden tuntematon on D.

Voi palvella sinua: Kertynyt taajuus: kaava, laskenta, jakauma, esimerkit

Sen löytämiseksi ehdotamme uutta suorakulmiokolmiota, joka muodostuu sen jälkeen, kun tikkaat liukastuivat vähän. Tässä kolmiossa on edelleen hypotenusa yhtä suuri kuin 10 m ja rinnakkainen cateto on nyt 6m + 3M = 9 m, siksi:

(H-d)² = 10² - 9² = 100 - 81 = 19

Korvaamme h = 8m, aikaisemmin laskettu:

(8-D)² = 19

Yhtälö voidaan ratkaista monin tavoin, mukaan lukien yleisen kaavan käyttö, jonka näytämme alla näillä vaiheilla:

Vaihe 1

Kehitä vasemmanpuoleinen huomattava vasemmisto:

64 -16d + D² = 19

Vaihe 2

Määritä toisen asteen yhtälö tuntemattomalle d:

d -d² - 16D + 45 = 0

Vaihe 3

-Kertoimet ovat: a = 1, b = -16 ja c = 45, korvaamme ne yleisessä kaavassa:

Yhtälön ratkaisut ovat:

d -d₁ = (16 + √76)/2 ≈ 12.36 m

d -d₂ = (16 - √76)/2 ≈ 3.64 m

Vaihe 4

Saadut ratkaisut analysoidaan: ensimmäisellä ei ole fyysistä järkeä, koska tikkaat eivät ole mahdollista kääntää 12.36 m, jos alun perin pysäkki oli 8 m korkealla maassa.

Siksi oikea vastaus on toinen ratkaisu: portaikon yläosa liukuu d = 3.64 m.

Voiko lukija ratkaista ongelman soveltamalla toista menetelmää?

Viitteet

1. Kalju. 1977. Perusalgebra. Venezuelan kulttuuriversiot.
2. Hoffman, J. Matematiikan aiheiden valinta. Nide 2.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Stewart, J. 2006. Precculment: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.
5. Zill, D. 1984. Algebra ja trigonometria. McGraw Hill.