Matematiikka

Bijektiivifunktio Mikä on, miten se tehdään, esimerkkejä, harjoituksia

Bijektiivifunktio Mikä on, miten se tehdään, esimerkkejä, harjoituksia

Eräs Bijektiivifunktio Se täyttää olemisen kaksinkertaisen kunto Injektio- ja liiallinen. Toisin sanoen kaikilla verkkotunnuksen elementeillä on yksi kuva codominiumissa, ja puolestaan ​​codominium on yhtä suuri kuin funktion alue ( R -F -A.

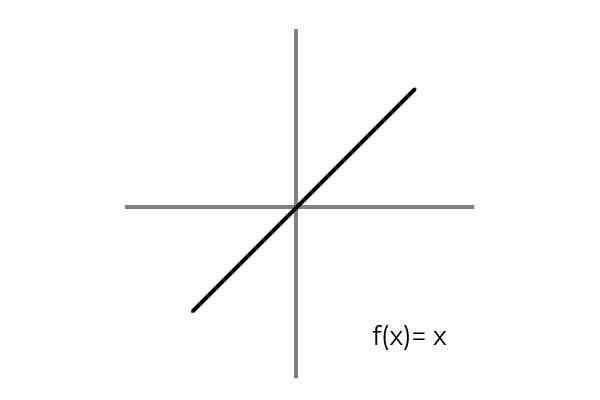
Se täyttyy, kun otetaan huomioon biunivocal -suhde domeenin elementtien välillä. Yksinkertainen esimerkki on toiminto F: r → R - linjalla määritelty F (x) = x

Lähde: Kirjoittaja

Havaitaan, että jokaiselle verkkotunnuksen tai lähtöjoukon arvolle (molemmat termit koskevat yhtäläisesti) Codominium- tai saapumisjoukossa on yksi kuva. Lisäksi ei ole mitään osaa codominiumista, joka ei ole kuva.

Täten F: r → R - linjalla määritelty F (x) = x on bijektiivi

[TOC]

Kuinka bijjective -toiminto on?

Tähän vastaamiseksi on tarpeen olla selkeitä käsitteitä, jotka liittyvät Injektiivisuus ja Funktion liiallisuus, Käsittelytoimintojen kriteerien lisäksi niiden mukauttamiseksi vaatimuksiin.

Funktion injektiivisuus

Toiminto on Injektiivinen Kun jokainen sen domeenin elementti liittyy yhteen Codominium -elementtiin. Codominium -elementti voi olla vain kuva yhdestä domeenin elementistä, tällä tavoin riippuvaisen muuttujan arvoja ei voida toistaa.

Harkita Injektiivinen Seuraavat on täytettävä funktioon:

∀ x1  ≠ x2   ⇒ f (x1 ) ≠ F (x2 -A

Funktion liiallisuus

Toiminto luokitellaan Liiallinen, Jos jokainen sen Codominium -elementti on ainakin yhden verkkotunnuksen elementin kuva.

Harkita Liiallinen Seuraavat on täytettävä funktioon:

Voi palvella sinua: Vaihtonäytteenotto

Olla F: DF → CF

∀ B ℮ CF  JA ℮  D -dF   / F (a) = b

Tämä on algebrallinen tapa selvittää, että jokaiselle C: lle kuuluu B -F On "a", joka kuuluu DF sellainen, että "A": ssä arvioitu funktio on yhtä suuri kuin "B". 

Toimintojen ilmastointi

Joskus funktio, joka ei ole Bijektiivi, voi käydä läpi tiettyjen ilmastointien. Nämä uudet olosuhteet voivat muuttaa sen a Bijektiivifunktio. Kaiken tyyppiset muutokset funktion verkkotunnukseen ja codominiumiin ovat päteviä, missä tavoitteena on täyttää injektiota ja yli -alkenitiivisuusominaisuuksia vastaavassa suhteessa.

Esimerkkejä: Ratkaisut harjoitukset

Harjoitus 1

Olla toiminto F: r → R - linjalla määritelty F (x) = 5x +1

V: [Kaikki todelliset numerot]

Havaitaan, että kaikissa verkkotunnusarvoissa on kuva codominiumissa. Tämä kuva on ainutlaatuinen, mikä tekee F ole yksi Injektiotoiminto. Samalla tavalla havaitsemme, että funktion codominium on yhtä suuri kuin sen alue. Täten täyttämällä ehto Liiallinen.

Injektio- ja liiallinen oleminen samanaikaisesti voimme päätellä sen

F: r → R - linjalla määritelty F (x) = 5x +1 on Bijektiivifunktio.

Tämä koskee kaikkia lineaarisia funktioita (toiminnot, joiden suurempi muuttujan aste on yksi).

Harjoitus 2

Olla toiminto F: r → R - määritelty F (x) = 3x2 - 2

Kun piirtät vaakaviivaa, havaitaan, että kaavio löytyy useammasta kuin yhdessä tilanteessa. Tämän vuoksi funktio F Se ei ole injektiivinen, joten se ei ole Bijektiivi Samalla kun se on määritelty R - → R -

Samoin on kodominium -arvoja, jotka eivät ole kuvia mistään verkkotunnuksen elementistä. Tämän vuoksi funktio ei ole liiallinen, mikä myös ansaitsee saapumisjoukon ehtoa.

Voi palvella sinua: Aseta teoria: Ominaisuudet, elementit, esimerkit, harjoitukset

Funktion verkkotunnus ja kodominium on ehdollinen

                                               F: [0 , ∞] → [ - 2 , ∞ -

Missä havaitaan, että uusi verkkotunnus kattaa arvot nollasta positiiviseen äärettömyyteen. Injektiivisuuteen vaikuttavien arvojen toistumisen välttäminen.

Siten kodominiumia on muokattu, laskemalla ”-2” positiiviseen äärettömyyteen eliminoimalla codominium-arvot, jotka eivät vastaa mitään domeenielementtiä

Tällä tavalla voidaan varmistaa F : [0 , ∞] → [ - 2 , ∞ - määritelty F (x) = 3x2 - 2

Se on bijektiivi

Harjoitus 3

Olla toiminto F: r → r määritelty F (x) = sin (x)

Välein [[ -∞ , +∞ - Sinusfunktio vaihtelee sen tuloksia nollan ja yhden välillä.

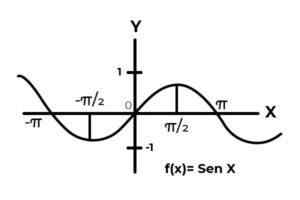Lähde: Kirjoittaja.

Toiminto F Se ei vastaa injektiivisuus- ja liiallisuuskriteerejä, koska riippuvat muuttujan arvot toistetaan jokainen π -aikaväli. Lisäksi välin ulkopuolella olevan codominiumin termit [-Eleven] Ne eivät ole kuvaa mistään verkkotunnuselemenistä.

Kun tutkitaan funktiografiikkaa F (x) = sin (x) Väliajoja havaitaan, jos käyrän käyttäytyminen täyttää kriteerit Bijektiivisuus. Kuten aikaväli  D -dF  = [[  π/2,3π/2  - Verkkotunnukselle. JA CF  = [-1, 1] Codominium.

Missä funktio vaihtelee välillä 1 --1, toistamatta mitään arvoa riippuvaisessa muuttujassa. Ja samanaikaisesti co -imeinium on yhtä suuri kuin lausekkeen käyttämät arvot Synti (x)

Tällä tavalla funktio F: [  π/2,3π/2  ] → [-1, 1]  määritelty F (x) = sin (x). Se on bijektiivi

Harjoitus 4

Nosta tarvittavat olosuhteet D: lleF ja cF. Niin että ilmaus

Voi palvella sinua: näytteenottovirhe: kaavat ja yhtälöt, laskenta, esimerkit

F (x) = -x2  Olla puolueena.

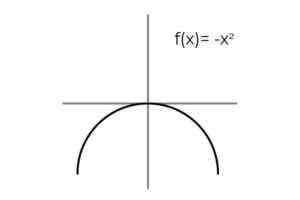Lähde: Kirjoittaja

Tulosten toisto havaitaan, kun muuttuja ottaa vastakkaiset arvot:

F (2) = f (-2) = -4

F (3) = f (-3) = -9

F (4) = f (-4) = -16

Verkkotunnus on ehdollinen, rajoittaen sen oikean viivan oikealle puolelle.

D -dF = [0 , +∞ -

Samoin havaitaan, että tämän funktion alue on aikaväli [[ -∞ , 0], joka palvelemalla codominium vastaa liiallisuusolosuhteita.

Tällä tavalla voimme päätellä sen

Ilmaisu F: [0 , +∞ ] → [ -∞ , 0] määritelty F (x) = -x2   Se on bijektiivi

Ehdotetut harjoitukset

Varmista, ovatko seuraavat toiminnot bijektiivi:

F: [0 , ∞) → R - määritelty F (x) = 3 (x + 1)2  +2

F: [ 3π/2,5π/2  ] → R määritelty F (x) = 5ctg (x)

F: [ -π,π  ] → R määritelty F (x) = cos (x - 3)

F: r → R - linjalla määritelty F (x) = -5x + 4

Viitteet

  1. Johdatus logiikkaan ja kriittiseen ajatteluun. Merrilee h. Lohi. Pittsburghin yliopisto
  2. Matemaattisen analyysin ongelmat. Piotr Bilar, Alfred Witkowski. Wroclawin yliopisto. Pylväs.
  3. Abstraktin analyysin elementit. Mícheál O'Searcoid PhD. Matematiikan laitos. University College Dublin, Beldfield, Dublind 4
  4. Johdatus logiikkaan ja deduktiivisten tieteiden metodologiaan. Alfred Tarski, New York Oxford. Oxford University Press.
  5. Matemaattisen analyysin periaatteet. Enrique Linés Escardó. Toimituksellinen palautus. Vuoteen 1991. Barcelona, ​​Espanja.