Monikulmiokaavio

Esimerkki monikulmiografiikoista. Lisenssillä

Mikä on monikulmainen grafiikka?

Eräs Monikulmiokaavio Se on lineaarinen kuvaaja. Toisin sanoen monikulmiokaavio on sellainen, joka löytyy Cartesian tasosta, jossa kaksi muuttujaa liittyy ja niiden välillä merkityt kohdat yhdistyvät jatkuvan ja epäsäännöllisen viivan muodostamiseksi.

Polygonaalinen kuvaaja saavuttaa histogrammin saman tarkoituksen, mutta se on erityisen hyödyllinen tietoryhmien vertaamisessa. Se on myös hyvä vaihtoehto osoittaa kumulatiiviset taajuusjakaumat.

Tässä mielessä termitaajuus ymmärretään, kun tapahtuma tapahtuu näytteen sisällä.

Kaikki monikulmaiset grafiikat on alun perin rakennettu histogrammeiksi. Tällä tavoin akseli on merkitty x: ksi (vaakasuora) ja akseliin y (pystysuora).

Jotkut muuttujat valitaan myös vastaavilla väliajoilla ja taajuuksilla tällaisten väliajojen mittaamiseksi. Yleensä muuttujat on merkitty x -tasoon ja taajuudet.

Kun X- ja Y -akselien muuttujat ja taajuudet on määritetty, pisteet, jotka yhdistävät ne tasossa. Nämä pisteet ovat myöhemmin yhtenäisiä, muodostaen jatkuvan ja epäsäännöllisen viivan, joka tunnetaan monikulmiona grafiikkana.

Monikulmainen graafinen toiminto

- Polygonaalisen kuvaajan päätehtävä on osoittaa ilmiön kärsimät muutokset määritellyllä ajanjaksolla tai suhteessa toiseen taajuuteen kutsuttuun ilmiöön.

- Se on hyödyllinen työkalu muuttujien tilaa ajassa tai toisin kuin muut tekijät.

Voi palvella sinua: Ryhmittelemättömän datan keskeiset taipumusmittaukset: Kaavat, harjoitukset

Joitakin yleisiä esimerkkejä, jotka voidaan osoittaa päivittäin.

- Yleisesti ottaen käytetään monikulmaista kuvaajaa, kun ilmiön variaatiossa on visuaalisesti edustettuna, tavoitteena määrittää samanvertaiset vertailut samasta.

Tämä kuvaaja on johdettu monissa histogrammin tapauksissa, koska Cartesian -tasossa merkityt kohdat vastaavat kohteita, jotka peittävät histogrammipalkit.

Esitys kaavio

Toisin kuin histogrammi, monikulmiokaavio ei käytä eri korkeuksia, muuttujien muutoksen merkitsemiseen määritellyn ajan kuluessa.

Kaavio käyttää linjasegmenttejä, jotka nousevat tai laskeutuvat Cartesian -tasoon, riippuen pisteistä, jotka merkitsevät muuttujien käyttäytymisen muutoksen sekä X -akselissa että ja in and and in the and in the and in the and in the and in the and in an and the- ja.

Tämän erityisyyden ansiosta monikulmiografiikka vastaanottaa nimensä, koska tuloksena oleva pisteiden liiton lukumäärä linjasegmenteillä Cartesian tasossa on monikulmio, jolla on peräkkäiset segmentit.

Tärkeä erityispiirte, joka on otettava huomioon, kun haluat edustaa monikulmaista kuvaajaa, on, että sekä X -akselin muuttujat että akselin taajuudet on merkitty niiden mittaamisen otsikolla.

Tällä tavalla kaavioon sisältyvien jatkuvien kvantitatiivisten muuttujien lukeminen on mahdollista.

Voi palvella sinua: Suhteellisuusvakio: Mikä on, laskenta, harjoitukset

Toisaalta, jotta voidaan tehdä monikulmainen kaavio, päihin on lisättävä kaksi väliaikaista, kukin niistä on yhtä suuri ja taajuus, joka vastaa nollaa.

Siten analysoidun muuttujan pää- ja pienempi raja otetaan ja kukin jaetaan kahdella, jotta voidaan määrittää paikka, jossa monikulmion graafisen linjan on käynnistettävä ja viimeistely.

Lopuksi kaavion pisteiden sijainti riippuu tiedoista, jotka on aiemmin otettu sekä muuttujasta että taajuudesta.

Nämä tiedot on järjestettävä pareittain, joiden sijainti Cartesian -lentokoneessa edustaa pistettä. Polygonaalisen kuvaajan muodostamiseksi pisteet on yhdistettävä suuntaan vasemmalta oikealle.

Esimerkkejä monikulmion grafiikasta

Esimerkki 1

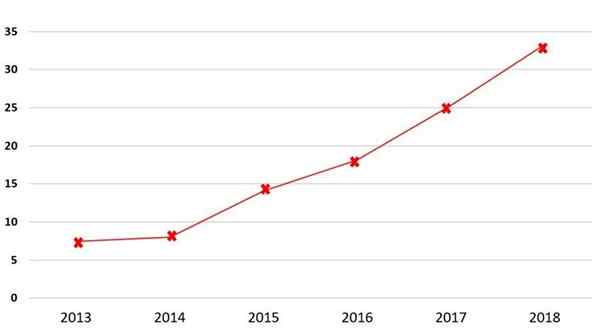Lähde: Josepicols123, CC BY-SA 4.0, Wikimedia Commons

Venezuelan työttömyysaste esitetään Nicolás Maduron toimeksiannolla vuosina 2013–2018 kansainvälisen valuuttarahaston tietojen mukaan.

Esimerkki 2

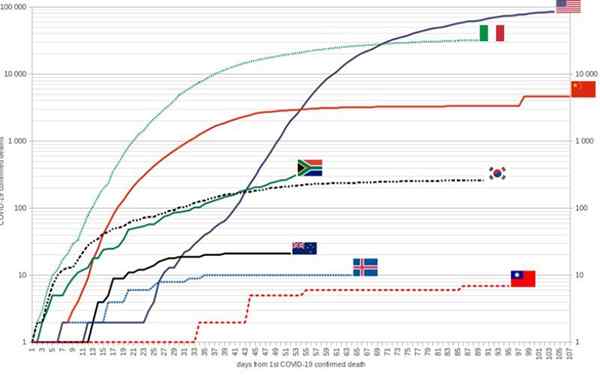Lähde: Jeandré du TOIT, CC BY-SA 4.0, Wikimedia Commons

Kaavio näyttää COVID-19: n kuolemat 8 maassa, ensimmäisestä vahvistetusta koronaviruksen kuolemasta vuoteen 2020 saakka.

Esimerkki 3

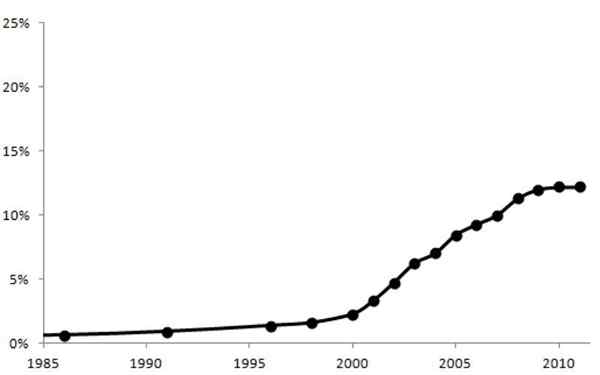Lähde: Davius, Wikimedia Commons

Kaavio osoittaa ulkomaisen väestön kasvun Espanjan kansallisen instituutin (INE) tietojen mukaan vuosina 1985-2010.

Viitteet

1. Taajuus monikulmio. Byjus.com
2. Taajuus monikulmio. Haettu OnlinestatBookista.com.