Hypercubo -määritelmä, mitat, koordinaatit, taitetut

Eräs hypercubo on ulottuvuus kuutio n. Dimension hypercubon erityistä tapausta kutsutaan Testaaja. Hypercubo tai N-CuBo koostuu suorista segmenteistä, kaikki saman pituudet, jotka ovat ortogonaalisia heidän kärjissä.

Ihmiset havaitsevat kolmen dimensionaalisen tilan: leveä, korkea ja syvyys, mutta meille ei ole mahdollista visualisoida yli 3 ulottuvuuden hypercubo. 

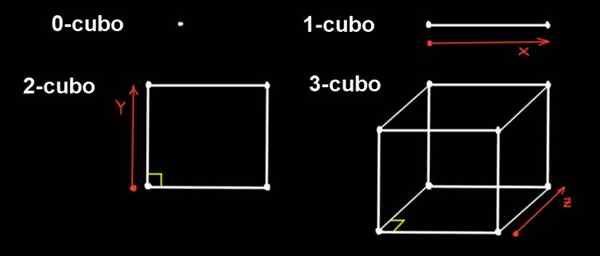
Kuvio 1. 0-kubo on piste, jos tämä piste ulottuu yhteen suuntaan etäisyydellä 1-kuutiotavalla, jos 1-kuutio ulottuu etäisyyteen ortogonaaliseen suuntaan, siellä on 2-kuutio (sivuista x A: iin), Jos 2-kuutio ulottuu etäisyyteen ortogonaaliseen suuntaan, on 3-kuutio. Lähde: f. Zapata.

Voimme tehdä ennusteita kolmen dimensionaalisessa tilassa edustamaan sitä, samanlainen kuin kuinka projisoimme kuutiota lentokoneessa edustamaan sitä edustamaan sitä.

Mitta 0 ainoa kuva on kohta, joten 0-kubo on piste. 1-kuutio on suora segmentti, joka muodostuu siirtämällä pisteen etäisyyteen etäisyyteen.

Puolestaan ​​2-kuutio on neliö. Se on rakennettu syrjäyttämällä 1-kuutio (segmentti pitkä a) suuntaan ja mikä on ortogonaalinen X-osoitteeseen, etäisyys.

3-kuutio on yleinen kuutio. Se on rakennettu neliöstä, joka syrjäyttää saman kolmanteen suuntaan (z), joka on ortogonaalinen X- ja Y -suuntiin, etäisyys -lla.

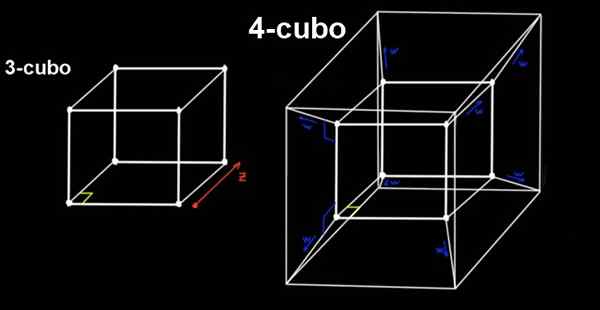Kuva 2. 4-kuutio (testiakti. Lähde: f. Zapata.

4-kuutio on koe, joka on rakennettu 3-kuutiosta, joka syrjäyttää saman ortogonaalisesti, etäisyys -lla, kohti neljättä ulottuvuutta (tai neljäs suuntaa), jota emme voi havaita.

Liipaisimella on kaikki suorat kulmat, siinä on 16 kärkeä ja kaikilla sen reunoilla (yhteensä 18) on sama pituus -lla.

Jos N-kubo- tai hypercubon reunojen pituus on 1, niin se on yksikkö hypercubo, jossa pisin diagonaalinen mittaa √n.

Voi palvella sinua: Lineaarinen ohjelmointi: Mihin se on, mallit, rajoitukset, sovelluksetKuva 3. N-kubo saadaan (n-1) -kuboolta, joka laajentaa sitä ortogonaalisesti seuraavassa ulottuvuudessa. Lähde: Wikimedia Commons.

[TOC]

Mitkä ovat mitat?

Mitat ovat vapauden asteet tai mahdolliset ohjeet, joissa esine voi liikkua.

Mitta 0 ei ole mahdollista liikkua, ja ainoa mahdollinen geometrinen objekti on kohta.

Euklidialaisen tilan ulottuvuutta edustaa suuntautunut viiva tai akseli, joka määrittelee kyseisen ulottuvuuden, nimeltään X -akseli. Kahden pisteen A ja B välinen ero on euklidian etäisyys:

D = √ [(x_-lla - x_{b -}-A²-. 

Kahdessa ulottuvuudessa tilaa edustaa kaksi ortogonaalista suuntautunutta viivaa toistensa kanssa, nimeltään X ja akseli.

Minkä tahansa pisteen sijainti tässä kahdessa dimensioisessa tilassa annetaan sen Cartesian -koordinaattiparilla (x, y) ja kahden pisteen A ja B välinen etäisyys on:

D = √ [(x_-lla - x_{b -}-A² + (ja_-lla - ja_{b -}-A²-

Koska se on tila, jossa euklidigeometria toteutetaan.

Kolmen ulottuvuuden tila

Kolmen dimensioinen tila on tila, jossa liikkumme. Sillä on kolme suuntaa: leveys, korkea ja syvyys.

Tyhjässä huoneessa kohtisuorat kulmat toistensa kanssa antavat nämä kolme suuntaa ja jokaiselle voimme yhdistää akselin: x, y, z.

Tämä tila on myös euklidian ja kahden pisteen A ja B välinen etäisyys lasketaan seuraavasti:

D = √ [(x_-lla - x_{b -}-A² + (ja_-lla - ja_{b -}-A² + (z_-lla - z -z_{b -}-A²-

Ihmiset eivät voi havaita enemmän kuin kolme alueellista mitat (tai euklideaa).

Tiukasti matemaattisesta näkökulmasta se on kuitenkin mahdollista.

Tässä tilassa pisteellä on koordinaatit: (x1, x2, x3, ..., xn) ja kahden pisteen välinen etäisyys on: 

D = √ [(x_Ensimmäinen - x_{1 b}-A² + (x_Toinen - x_2b-A² +... + (x_naa - x_HUOM-A²-.

Voi palvella sinua: hypergeometrinen jakauma: kaavat, yhtälöt, malli

Neljäs ulottuvuus ja aika

Itse asiassa suhteellisuusajan teoriassa käsitellään vielä yhtenä ulottuvuutena ja koordinaatti liittyy.

Mutta on selvennettävä, että tämä ajan liittyvä koordinaatti on kuvitteellinen numero. Siksi kahden pisteen tai tapahtuman erottaminen avaruusajassa ei ole euklidiana, vaan seuraa Lorentzin metriä.

Neliulotteinen hypercubo (liipaisin) ei elä avaruusaikana, kuuluu neliulotteiseen euklideaaliseen hyper-avaruuteen. 

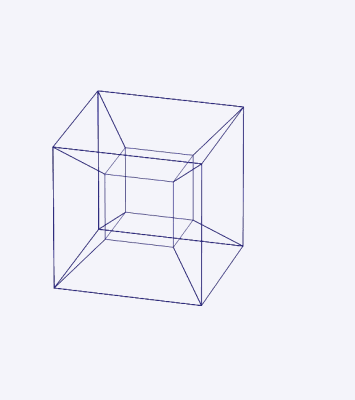
Kuva 4. Neljän dimensionaalisen hypercubon 3D -projektio yksinkertaisessa kierroksessa tason ympärillä, joka jakaa etukuvion vasemmalle, takaisin oikealle ja ylhäältä alas. Lähde: Wikimedia Commons.

Hypercubon koordinaatit

Alkuperäiseen keskittyneen N-kubo-kärjen koordinaatit saavutetaan tekemällä kaikki seuraavan lausekkeen mahdolliset permutaatiot:

(A/2) (± 1, ± 1, ± 1, .. ., ± 1)

Missä a on reunan pituus.

-Hän tilavuus Reunan a on: (A/2)ⁿ (2ⁿ) = aⁿ.

-Se pisin diagonaali Se on etäisyys vastakkaisten kärkien välillä.

-Seuraavat ovat vastakkaiset kärkipisteet neliössä: (-1, -1) ja (+1, +1).

-Ja a Kuutio: (-1, -1, -1) ja (+1, +1, +1). 

-Se pisin diagonaali N-kubo-toimenpiteistä: 

D = √ [1 -(-1))² +… + (1 -(-1))²] = √ [n 2²] = 2√n

Tässä tapauksessa oletetaan, että sivu on A = 2. N-kubo-puolelle kenelle tahansa pysyy:

d = a√n.

-Kokeessa on jokainen sen 16 kärjestä kytketty neljään reunaan. Seuraava kuva osoittaa, kuinka kärkipisteet on kytketty liipaisimeen.

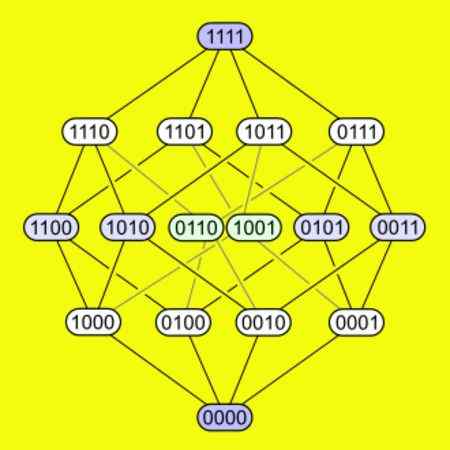Kuva 5. Neljän ulottuvuuden hypercubon 16 kärkipistettä esitetään ja kuinka ne yhdistävät saman. Lähde: Wikimedia Commons.

Hypercubo

Säännöllinen geometrinen luku, esimerkiksi monikulmio, voidaan avata useissa alemman ulottuvuuden lukuissa.

2-kuutiota (neliö) voidaan avata neljään segmenttiin, ts. Neljä 1-kuutiota.

Se voi palvella sinua: Poisson -jakelu: kaavat, yhtälöt, malli, ominaisuudet

Samoin 3-kuutio voidaan avata kuudessa 2-kuutiossa.

Kuva 6. N-kubo voidaan avata useissa (N-1) -kuboissa. Lähde: Wikimedia Commons.

4-kuutio (testaatti) voidaan avata kahdeksassa 3-kuutiossa.

Seuraava animaatio osoittaa tripin avautumisen.

Kuva 7. 4 -dimensioinen hypercubo voidaan avata kahdeksassa kolmen dimensionaalisessa kuutiossa. Lähde: Wikimedia Commons. Kuva 8. Neljän dimensionaalisen hypercubon kolmen dimensioinen projektio, joka tekee kaksinkertaisen kierroksen kahden ortogonaalisen tason ympärillä. Lähde: Wikimedia Commons.

Viitteet

1. Tieteellinen kulttuuri. Hypercubo, visualisoimalla neljäs ulottuvuus. Haettu: Culturacientifica.com
2. Epsilones. Tetradimensionaalinen hypercubo tai tesseract. Toipunut: Epsilones.com
3. Perez R, Aguilera a. Menetelmä tutkimuksen saamiseksi hypercubon (4d) kehityksestä (4d). Toipunut: ResearchGate.netto
4. Wikilibros. Matematiikka, polyhedra, hypercubes. Palautettu: on.Wikibooks.org
5. Wikipedia.  Hyperkuutio. Haettu: vuonna.Wikipedia.com
6. Wikipedia. Tesserakti. Haettu: vuonna.Wikipedia.com