Magneettiset induktiokaavat, miten se lasketaan ja esimerkkejä

Se magneettinen induktio tai magneettinen vuon tiheys on ympäristön muutos, joka johtuu sähkövirtojen läsnäolosta. He muokkaavat ympäröivän tilan luonnetta, luomalla a ala Vektori.

Vektori Magneettinen induktio, magneettinen vuon tiheys Tai yksinkertaisesti magneettikenttä B -, Sillä on kolme erottuvaa ominaisuutta: intensiteetti, joka ilmaistaan ​​numeerisella arvolla, osoitteella ja myös avaruuskohdassa annetulla mielellä. Se on korostettu lihavoituna erottamaan se puhtaasti numeerisista määristä tai skalaarista.

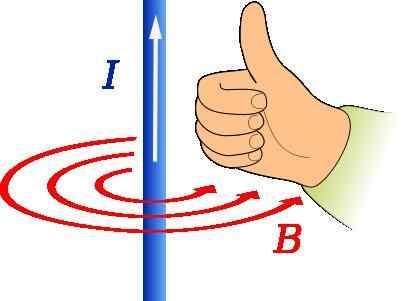Oikean peukalon sääntö magneettisen induktiovektorin suunnan ja suunnan määrittämiseksi. Lähde: Jfmelero [CC BY-SA 4.0 (https: // creativecommons.Org/lisenssit/by-SA/4.0)]

Oikea peukalosääntöä käytetään magneettikentän suunnan ja suunnan löytämiseen, joka on peräisin virtaa kuljettavasta johdosta, kuten yllä olevassa kuvassa esitetään.

Oikean käden peukalon tulisi osoittaa virran suuntaan. Sitten jäljellä olevien sormien käännös osoittaa B -, että kuvassa edustaa samankeskiset punaiset ympyrät.

Tässä tapauksessa osoite B - Se on tangentiaalinen johdon kanssa tapahtuvalle kehälle ja merkitys on kellojen kädet ristiriidassa.

Se magneettinen induktio B - Kansainvälisessä järjestelmässä Tesla (T) mitataan, mutta on yleisempää mitata sitä toisessa Gauss -yksikössä (g). Molemmat yksiköt nimitettiin vastaavasti Nikola Teslan (1856-1943) ja Carl Friedrich Gaussin (1777-1855) kunniaksi heidän poikkeuksellisesta panoksestaan ​​sähkön ja magnetismin tieteeseen.

[TOC]

Mitkä ovat magneettisen induktion tai magneettisen vuon tiheyden ominaisuudet?

Kompassi, joka on sijoitettu langan lähellä virran kanssa, kohdistuu aina B -. Tanskalainen fyysikko Hans Christian Oersted (1777-1851) oli ensimmäinen, joka toteutti tämän ilmiön 1800-luvun alussa.

Voi palvella sinua: areolaarinen nopeus: miten se lasketaan ja ratkaistu harjoitukset

Ja kun virta lakkaa, kompassi osoittaa maantieteelliseen pohjoiseen, kuten aina. Vaihtamalla kompassin varovasti, kartta saadaan magneettikentän muodosta.

Tällä kartalla on aina samankeskisten ympyröiden muoto johtoon, kuten alussa on kuvattu. Tällä tavalla se voidaan visualisoida B -.

Vaikka lanka ei olisi suora, vektori B - muodostaa samankeskiset ympyrät sen ympärille. Sen määrittämiseksi, mikä kentällä on, riittää kuvitella hyvin pieniä vaijeregmenttejä, niin pieniä, että ne vaikuttavat suoraviivaisilta ja samankeskisten kehysten ympäröimänä.

Magneettikenttälinjat, jotka tuottavat virtaa kuljettaa langan silmukka. Lähde: Pixabay.com

Tämä osoittaa magneettikenttälinjojen tärkeän ominaisuuden B -: Heillä ei ole periaatetta tai loppua, he ovat aina suljettuja käyriä.

Biot-Savart-laki

Yhdeksästoista vuosisataa määritti tieteen sähkön ja magneettisuuden aikakauden alun. Lähellä vuotta 1820 ranskalaiset fyysikot Jean Marie Biot (1774-1862) ja Felix Savart (1791-1841) löysivät lain, joka kantaa hänen nimensä ja joka mahdollistaa vektorin laskemisen B -.

He tekivät seuraavat havainnot vaikutuksesta magneettikenttään, joka on tuotettu differentiaalipituuden lanka -segmentissä DL joka kuljettaa sähkövirran Yllyttää-

• Suuruus B - vähenee käänteisen etäisyyden neliön kanssa johdin (tämä on järkevää: kaukana johtimesta B - Sen on oltava vähemmän kuin läheisissä kohdissa).
• Suuruus B - Se on verrannollinen virran voimakkuukseen Yllyttää Se kulkee langalla.
• Osoite B - Se on tangentiaalinen radion ympärysmitta r - keskitetty johtoon ja suuntaan B - Se on annettu, kuten sanoimme, oikealla peukalon sääntöllä.

Vektori tai tuotteen ristituote on sopiva matemaattinen työkalu viimeisen pisteen ilmaisemiseksi. Vektorituotteen luomiseksi tarvitaan kaksi vektoria, jotka määritellään seuraavasti:

• d -dlens Se on vektori, jonka suuruus on differentiaalisegmentin pituus DL
• r - Se on vektori, joka siirtyy langasta pisteeseen, josta haluat löytää kentän

Voi palvella sinua: Sähkömagneettinen spektri: Ominaisuudet, kaistat, sovellukset

Kaavat

Kaikki tämä voidaan yhdistää matemaattisessa ilmaisussa:

Tasa -arvon määrittämiseksi tarvittava suhteellisuusvakio on Vapaan tilan magneettinen läpäisevyys μ_jompikumpi  = 4π.10^-7 T.m/a

Tämä lauseke on Biotin ja Savartin laki, jonka avulla voit laskea nykyisen segmentin magneettikentän.

Tällaisen segmentin puolestaan ​​on oltava osa suurempaa ja suurempaa piiriä: virranjakauma.

Edellytys, että piiri on suljettu, on välttämätöntä sähkövirran virtaamiseksi. Sähkövirta ei voi virtaa avoimissa piireissä.

Lopuksi tämän virran jakauman kokonaismagneettikentän löytämiseksi lisätään kaikki kunkin differentiaalisegmentin vaikutukset d -dlens. Tämä vastaa kaiken jakelun integrointia:

Biot-Savart-lain soveltamiseksi ja magneettisen induktiovektorin laskemiseksi on tarpeen harkita erittäin tärkeitä tärkeitä kohtia:

• Vektorituote kahden vektorin välillä johtaa aina toiseen vektoriin.
• Biot-Savart-lain vektorituotteen suuruus on:missä θ on kulma d -dlens ja r -.
• Vektorituote olisi löydettävä ennen Jos kiinteä resoluutio ratkaistaan, kunkin erikseen saatujen komponenttien integraali ratkaistaan.
• On välttämätöntä piirtää tilanne ja luoda riittävä koordinaattijärjestelmä.
• Aina kun jonkin symmetrian olemassaoloa havaitaan, sitä on käytettävä laskenta -ajan tallentamiseen.
• Kun kolmioita on, Pythagoras -lause ja kosinin lause ovat suuria apua muuttujien geometrisen suhteen luomiseksi.

Kuinka se lasketaan?

Käytännöllisellä esimerkillä laskelmasta B - Strektilinariseen johdolle nämä suositukset sovelletaan.

Se voi palvella sinua: Täsmällinen kuorma: Ominaisuudet ja Coulomb Law

Esimerkki

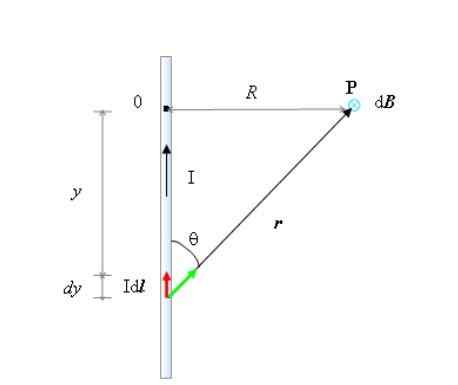
Laske magneettikentän vektori, jonka erittäin pitkä suorakulmainen johdin tuottaa tilan pisteessä P, esitetyn kuvan mukaan.

Geometria, joka on tarpeen magneettikentän laskemiseksi pisteessä P, äärettömän pitkän virran johdin. Lähde: Itse tehty.

Kuvasta sinun täytyy:

• Lanka on suunnattu pystysuunnassa, virtaan virtaavan virran. Tämä osoite on +ja koordinaattijärjestelmässä, jonka alkuperä on pisteessä tai.
• θ on kulma d -dlens ja r - Ja on myös totta, että: 
• Tässä tapauksessa oikean peukalon säännön mukaan, B - Kohdassa P on suunnattu paperiin, joten se on merkitty pienellä ympyrällä ja "x" kuvassa. Tämä osoite pidetään -z.
• Oikea kolmio, jonka jalat ovat ja ja R -, liittyy molemmat muuttujat Pythagoras -lauseen mukaan: r -²= R²+ja²

Kaikki tämä korvataan olennaisesti. Vektori- tai ristituote on merkitty sen suuruudella plus -suunta ja sen merkitys:

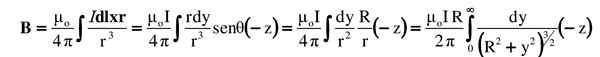
Ehdotettu integraali haetaan integraalitaulukossa tai se ratkaistaan ​​sopivalla trigonometrisella korvauksella (lukija voi tarkistaa tuloksen käyttämällä y = rtg θ)-

Tulos on yhtä mieltä odotettavissa olevista: kentän suuruus vähenee etäisyyden R kanssa ja kasvaa suhteessa virran I voimakkuuden kanssa.

Vaikka äärettömän pitkä lanka on idealisointi, saatu lauseke on erittäin hyvä lähestymistapa pitkän johdon kentälle.

BIOT- ja Savart -lain kanssa on mahdollista löytää muiden korkean symmetriajakauman magneettikenttä, kuten pyöreä spiraali, joka kuljettaa virtaa tai taitettuja johtoja, joissa yhdistyvätisstrilineaariset ja kaarevat segmentit yhdistävät.

Tietysti integroidun analysoimiseksi ongelmalla on oltava korkea symmetria. Muuten vaihtoehto on ratkaiseva integraali numeerisesti.

Viitteet

1. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Nide 2. Meksiko. Cengage Learning Editors. 367-372.