Ortogonaaliset matriisiominaisuudet, esittely, esimerkit

Sinulla on yksi Ortogonaalinen matriisi Kun mainittu matriisi kerrottuna sen siirtämisellä johtaa identiteettimatriisiin. Jos matriisin käänteinen on yhtä suuri kuin siirretty, alkuperäinen matriisi on ortogonaalinen.

Ortogonaaliset matriisit ovat ominaista, että rivien lukumäärä on yhtä suuri kuin sarakkeiden lukumäärä. Lisäksi rivivektorit ovat yksikön ortogonaalisia vektoreita ja myös transposoidun vektorien ihottuma.

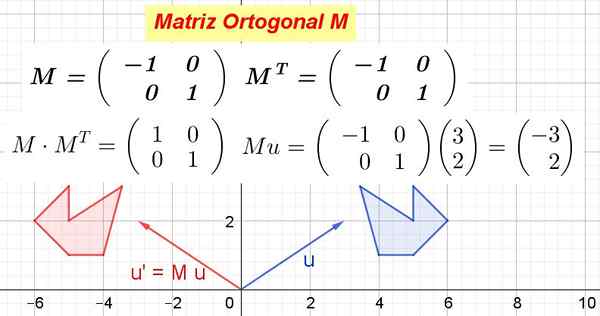Kuvio 1. Esimerkki ortogonaalisesta matriisista ja siitä, kuinka geometriset objektit muuttavat. (Valmistaja Ricardo Pérez)

Kun ortogonaalinen matriisi kerrotaan vektoritilan vektoreilla isometrinen muutos, toisin sanoen muutos, joka ei muuta etäisyyksiä ja säilyttää kulmat.

Ortogonaalisten matriisien tyypillinen edustaja on kiertomariisit. Ortogonaalisten matriisien muutoksia vektoritilassa kutsutaan Ortogonaaliset muutokset.

Kartesialaisten vektorien edustamat kierto- ja heijastus geometriset muunnokset tehdään soveltamalla alkuperäisiin vektoriin ortogonaalisia matriiseja, jotta saadaan muunnettujen vektorien koordinaatit. Tästä syystä ortogonaalisia matriiseja käytetään laajasti laskennallisessa graafisessa prosessoinnissa.

[TOC]

Ominaisuudet

Taulukko M Se on ortogonaalinen, jos se kerrotaan sen siirtämällä M^T Identiteettimatriisi johtaa Yllyttää. Samoin ortogonaalisen matriisin siirron tuote identiteettimatriisin alkuperäisellä matriisilla:

M m^T = M^T M = i

Edellisen lausunnon seurauksena ortogonaalisen matriisin siirretty on yhtä suuri kuin sen käänteinen matriisi:

M^T = M^-1.

Ortogonaalisen ulottuvuuden matriisien joukko n x n Ne muodostavat ortogonaalisen ryhmän Tai (n). Ja osa Tai (n) Ortogonaalisten matriisien määrittämisellä +1 muodostavat Erityinen matriisiryhmä sen (n). Ryhmän matriisit Sinun (n) Ne ovat matriiseja, jotka tuottavat lineaarista kiertomuutoksia, tunnetaan myös nimellä Kiertoryhmä.

Esittely

Osoitamme, että matriisi on ortogonaalinen, jos ja vain jos rivivektorit (tai pylväsvektorit) ovat ortogonaalisia toisiinsa ja normi 1.

Voi palvella sinua: Bayes -lause

Oletetaan. Jos sitä merkitään v1, v2,.. ., vn N -vektorit täyttyy:

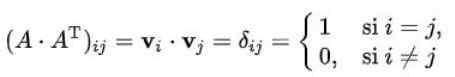
Missä on selvää, että rivivektorien joukko on joukko ortogonaalisia vektoreita, joilla on normi.

Esimerkit

Esimerkki 1

Osoita, että vektorilla on 2 x 2 -matriisi ensimmäisessä rivissä V1= (-1 0) ja toisessa rivissä vektori V2= (0 1) on ortogonaalinen matriisi.

Ratkaisu: Matriisi on rakennettu M ja sen siirto lasketaan M^T-

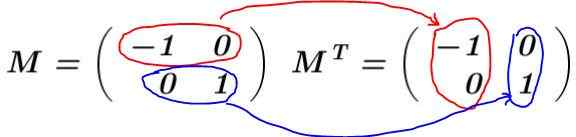
Tässä esimerkissä matriisi M Se on siirretty auto, toisin sanoen, että matriisi ja sen siirto ovat identtisiä. Se moninkertaistaa M sen siirtämiseksi M^T-

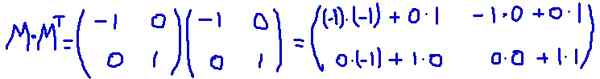
Se on varmistettu M M^T Se on yhtä suuri kuin identiteettimatriisi:

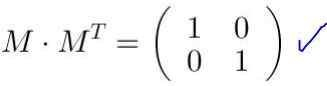
Kun matriisi M Se kerrotaan vektorin tai pisteen koordinaateilla, saadaan uusia koordinaatit, jotka vastaavat matriisin tekemistä muunnosta.

Kuvio 1 näyttää miten M Muuttaa vektoria tai sisään tai' Ja myös kuten M Muuta sininen monikulmio punaiseksi monikulmioksi. Kuten M Se on ortogonaalinen, se on sitten ortogonaalinen muutos, joka säilyttää etäisyydet ja kulmat.

Esimerkki 2

Oletetaan, että seuraavalla lausekkeella on määritelty 2 x 2 -matriisi:

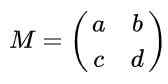
Löytää todelliset arvot -lla, b -, c ja d -d niin että matriisi M Olla ortogonaalinen matriisi.

Ratkaisu: Määritelmän mukaan matriisi on ortogonaalinen, jos se kerrottuna sen siirtämisellä saadaan sen seurauksena identiteettimatriisi. Muistaminen, että siirretty matriisi saadaan alkuperäisestä, sarakkeiden vaihtaminen on seuraava tasa -arvo:

Se voi palvella sinua: funktion verkkotunnus ja ristiriita (esimerkkien kanssa)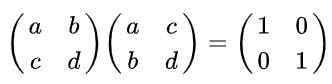

Matriisin kertolasku on:

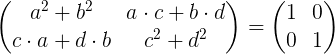
Vastaten vasemman matriisin elementit oikealla olevan identiteettimatriisin elementtien kanssa, saadaan neljän yhtälön järjestelmän, jossa on neljä tuntematonta A, B, C ja D.

Ehdotamme A, B, C ja D seuraavia lausekkeita, jotka perustuvat trigonometrisiin syihin sinus ja kosini:

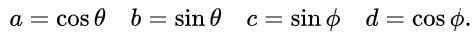
Tämän ehdotuksen ja perusteellisen trigonometrisen identiteetin vuoksi matriisielementtien tasa -arvon ensimmäinen ja kolmas yhtälö tyydytetään automaattisesti. Kolmas ja neljäs yhtälö ovat samat ja matriisin tasa -arvossa ehdotettujen arvojen korvaamisen jälkeen on tällainen:

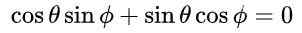
Mikä johtaa seuraavaan ratkaisuun:

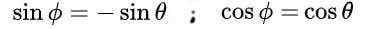
Lopuksi saadaan seuraavat ratkaisut ortogonaaliselle matriisille m:

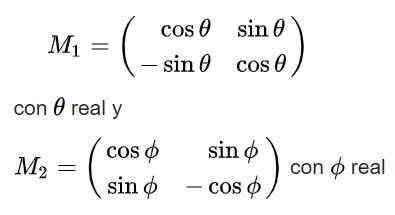
Huomaa, että ensimmäisellä ratkaisuilla on determinantti +1, joten se kuuluu sen ryhmään (2), kun taas toisella ratkaisulla on determinantti -1, ja siksi se ei kuulu tähän ryhmään.

Esimerkki 3

Seuraavan matriisin perusteella löydä A- ja B -arvot, jotta sinulla olisi ortogonaalinen matriisi.

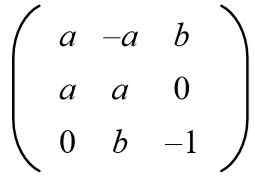
Ratkaisu: Jotta tiety. Sitten siirretyllä matriisilla annetun matriisin matriisituote tehdään seuraavaksi: seuraavaksi:

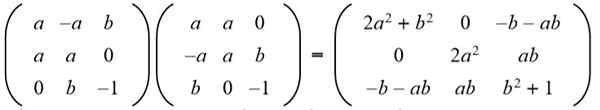
Seuraavaksi tulos sovitetaan identiteettimatriisiin 3 x 3:

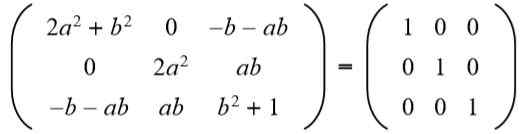
Toisessa rivin kolmannessa sarakkeessa (A b = 0), mutta -lla Se ei voi olla nolla, koska jos niin, toisen rivin ja toisen sarakkeen elementtien tasa -arvo ei toteuteta. Silloin välttämättä B = 0. Korvaaminen b - Arvolle 0 meillä on:

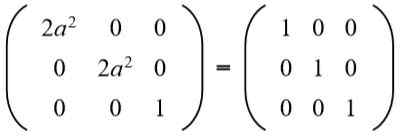
Sitten yhtälö ratkaistaan: 2a^2 = 1, Kenen ratkaisut ovat: +½√2 ja -½√2.

Voi palvella sinua: kulmat, ominaisuudet ja esimerkit

Positiivinen ratkaisu -lla Se johtaa seuraavaan ortogonaaliseen matriisiin:

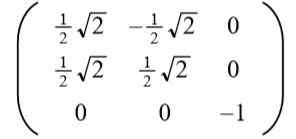
Lukija voi helposti varmistaa, että rivivektorit (ja myös sarakevektorit) ovat ortogonaalisia ja yksikköä, toisin sanoen Ortonormal.

Esimerkki 4

Osoita, että matriisi -Lla Kenen rivit ovat V1 = (0, -1 0), V2 = (1, 0, 0) ja V3 = (0 0 -1) Se on ortogonaalinen matriisi. Lisäksi löydä kuinka kanonisen pohjan vektorit muuttuvat I J K Vektoreille U1, U2 ja U3.

Ratkaisu: On muistettava, että matriisin elementti (i, j) kerrottuna sen siirrolla, on rivinvektorin skalaarituote (i) transpose -sarakkeella (J). Lisäksi tämä tuote on yhtä suuri kuin Kroneckerin suisto, jos matriisi on ortogonaalinen:

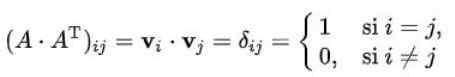
Meidän tapauksessamme se on näin:

V1 • V1 = 0x0 + (-1) x (-1) + 0x0 = 1

V2 • V2 = 1 × 1 + 0x0 + 0x0 = 1

V3 • v3 = 0x0 + 0x0 + (-1) x (-1) = 1

V1 • v2 = 0x1 + (-1) x0 + 0x0 = 0

V2 • V1 = 1 × 0 + 0x (-1) + 0x0 = 0

V2 • v3 = 1 × 0 + 0x (0) + 0x (-1) = 0

V3 • v2 = 0x1 + 0x (0) + (-1) x0 = 0

V1 • V3 = 0x0 + (-1) x (0) + 0x (-1) = 0

V3 • v1 = 0x0 + 0x (-1) + (-1) x0 = 0

Mitä osoitetaan, että se on ortogonaalinen matriisi.

sitä paitsi u1 = a i = (0, 1, 0); U2 = a J = (-1, 0, 0) ja lopulta U3 = a k = (0, 0, -1)

Viitteet

1. Anthony Nicolaides (1994) determinantit ja matriisit. Pass -julkaisu.
2. Birkhoff ja Maclane. (1980). Moderni algebra, Ed. Vicens-Vives, Madrid.
3. Casteleiro Villalba m.  (2004) Johdanto lineaariseen algebraan. ESIC -toimitus.
4. Dave Kirkby (2004) Maths Connect. Heinemann.
5. Jenny Olive (1998) Matematiikka: Opiskelijan selviytymisopas. Cambridge University Press.
6. Richard J. Brown (2012) 30 sekunnin matematiikka: 50 mielenterveysteoriaa matematiikassa. Ivy Press Limited.
7. Wikipedia. Ortogonaalinen matriisi. Palautettu: on.Wikipedia.com
8. Wikipedia. Ortogonaalinen matriisi. Haettu: vuonna.Wikipedia.com