Tachtenberg -menetelmä Mikä on, esimerkkejä

Hän Trachtenberg -menetelmä Se on järjestelmä aritmeettisten operaatioiden, lähinnä kertolaskujen suorittamiseksi, helposti ja nopealla tavalla, kun niiden säännöt ovat tiedossa ja hallitsevia.

Venäläinen insinööri Jakow Trachtenberg (1888-1953) suunnitteli hänet, kun hän oli natsien vanki keskitysleirillä, häiriötekijänä terveyden ylläpitämiseksi, kun hän jatkoi vankeutta.

Kuvio 1. Kertolasku. Lähde: Wikimedia Commons. Taulacat [CC BY-SA 3.0 (https: // creativecommons.Org/lisenssit/by-SA/3.0)] [TOC]

Mikä on etuja ja haittoja

Tämä menetelmä edustaa, että kertoimien suorittaminen se ei ole välttämätöntä.

Haittana on, että millään luvulla ei ole yleistä sääntöä, mutta sääntö vaihtelee kertoimen mukaan. Kuvioita ei kuitenkaan ole vaikea muistaa, ja periaatteessa sallivat operaatiot ilman paperia ja lyijykynää.

Koko tämän artikkelin ajan keskitymme säännöihin, jotka kertovat nopeasti.

[TOC]

Esimerkit

Menetelmän soveltamiseksi on tarpeen tietää säännöt, joten esittelemme ne yksitellen ja esimerkkejä:

- Kerro kuva 10 tai 11

Kertolasku 10: llä

-Mitä tahansa lukua 10: llä, nolla lisätään yksinkertaisesti oikealle. Esimerkiksi: 52 x 10 = 520.

Säännöt moninkertaisesti 11: llä

-Nolla lisätään kuvan alkuun ja lopussa.

-Jokainen numero lisätään oikeanpuoleisella naapurillaan ja tulos on sijoitettu alkuperäisen kuvan vastaavan numeron alapuolelle.

-Jos tulos ylittää yhdeksän, yksikkö merkitään ja on asetettu pieni kohta muistaa, että meillä on yksikkö, joka lisätään seuraavan kuvan summaan oikealla naapurillaan.

Yksityiskohtainen kertolasku 11: llä

Kerro 673179 11: llä

Voi palvella sinua: lähentymisradio: Määritelmä, esimerkit ja harjoitukset ratkaistu

0 -6731790 x 11 =

--

= 7404969

Vaadittavat vaiheet tämän tuloksen saavuttamiseksi, jotka on kuvattu värien kautta, ovat seuraavat:

-Kertoimen yksikön (11) 1 kerrottiin kertoimella 9 (06731790) ja se lisättiin 0. Yhtenäisyysnumero saatiin: 9.

-Sitten se moninkertaistaa 1 x 7 ja lisää yhdeksän antaa 16 ja meillä on 1, kymmenkunta numero on sijoitettu: 6.

-Kerro sitten 1: llä 1: llä lisätään oikean 7 plus 1: n naapuri, joka johti seurauksena 9 Sata.

-Seuraava luku saadaan kertomalla 1 1: llä plus naapurimaiden 1, se tulokset 4 Tuhansien numeroiden.

-Se kerrotaan 1: 1 ja naapuri lisätään tuloksena 10, nolla sijoitetaan (0 -) Tithe -numerona ja se vie yhden.

-Sitten 1 6 plus naapuri 7 on 13 plus 1, joka oli 14, 4 sadan tuhannen numerona ja ottaa 1.

-Lopuksi kerro 1 nolla, joka lisättiin alkuun, antaen nollaa enemmän naapuri 6 plus yksi, joka otti. Se on vihdoin 7 Miljoonia vastaavalle numerolle.

- Kertolasku numeroilla 12 - 19

Kerrotaan 12: lla 

-Alkuun lisätään nolla ja toinen nolla kuvan lopussa moninkertaisesti.

-Jokainen numero kaksinkertaistetaan kerroksesta kerrottuna ja lisää oikean naapurinsa kanssa.

-Jos summa ylittää 10, yksikkö lisätään seuraavaan päällekkäisyyteen ja lisää naapurin kanssa.

Esimerkki kertolaskusta 12: lla

Kerro 63247 12: lla

0 -632470 x 12 =

-

758964

Yksityiskohdat tämän tuloksen saavuttamiseksi, tiukasti noudattavien sääntöjen mukaisesti, esitetään seuraavassa kuvassa:

Kuva 2. Trachtenberg -menetelmä moninkertaistaaksesi minkä tahansa numeron 12: lla. Lähde: f. Zapata.

- Kertomussääntöjen laajentaminen 13: lla ..

Kerroinmenetelmä 12: lla voidaan laajentaa kertolaskuihin 13, 14 asti 19: een yksinkertaisesti muuttaa kolmentoista tapauksen päällekkäisyyttä, nelinkertaisesti 14 ja niin edelleen, kunnes se on saavuttanut 19.

Voi palvella sinua: Ortogonaalinen matriisi: Ominaisuudet, esittely, esimerkit

Tuotteiden säännöt 6, 7 ja 5

- Kertolasku 6: lla

-Lisää nollat ​​kuvan alkuun ja loppuun kerrottuna 6: lla.

-Lisää puolet oikealta oikealta jokaiselle numerolle, mutta jos numero on outo lisätä 5.

Kuva 3. Kuvion kertominen 6: lla, Trachtenberg -menetelmän mukaisesti. Lähde: f. Zapata.

- Kertolasku 7

-Lisää nollat ​​kuvan alkuun ja lopussa moninkertaistaa.

-Kopioi kukin numero ja lisää naapurin alaosa, mutta jos numero lisätään lisäksi 5.

Esimerkki kertolaskusta 7

-Kerro 3412 7: llä

-Tulos on 23884. Sääntöjen soveltamiseksi on ensin suositeltavaa tunnistaa parittomat numerot ja asettaa pieni 5 muistaaksesi tämän luvun lisääminen tulokseen.

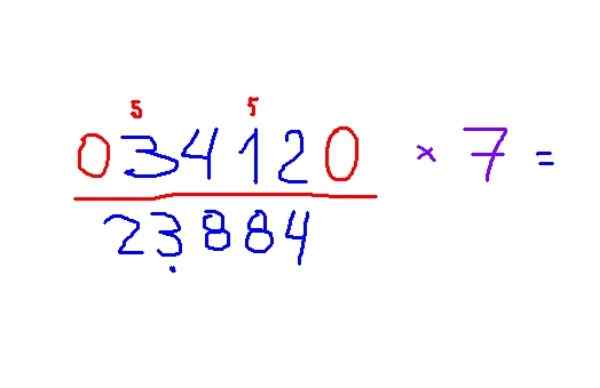Kuva 4. Esimerkki Kuvan kertolasku 7: llä, Trachtenbergin menetelmän mukaan. Lähde: f. Zapata.

- Kertolasku 5

-Lisää nollat ​​kuvan alkuun ja lopussa moninkertaistaa.

-Aseta jokaisen naapurin alaosan alle oikealla puolella, mutta jos numero on pariton lisäksi 5.

Esimerkki kertolasku 5

Kerro 256413 5: llä

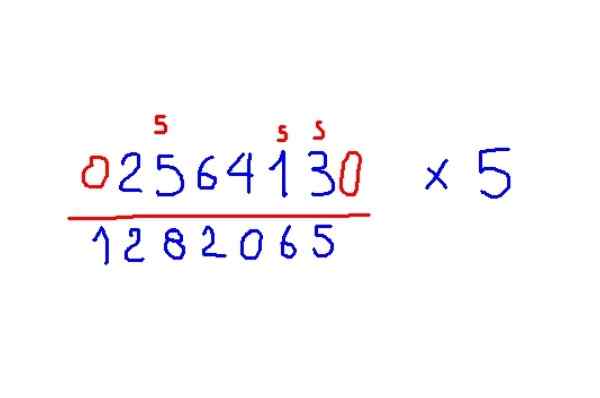Kuva 5. Esimerkki Kuvan kertolasku 5: llä, Trachtenberg -menetelmän mukaan. Lähde: f. Zapata.

Tuotesäännöt 9: llä

-Alkuun lisätään nolla ja toinen kuvan lopussa kerrotaan yhdeksällä.

-Ensimmäinen numero oikealle saadaan vähentämällä kuvan vastaava numero moninkertaiseksi.

-Sitten seuraava numero vähennetään ja naapuri lisätään.

-Edellinen vaihe toistetaan, kunnes saavutat kertomuksen nollan, missä vähennämme 1 naapurista ja tulos kopioidaan nollan alapuolelle.

Voi palvella sinua: mitkä ovat 30? (Selitys)

Esimerkki kertolaskusta 9

Kerro 8769 9: llä:

087690 x 9 =

--

78921

Toimenpide

10 - 9 = 1

(9-6) + 9 = 12 (( 2 Ja se vie 1)

(9-7)+1+6 =9

(9-8) +7 =8

(8-1) = 7

Kertolasku 8, 4, 3 ja 2

-Lisää nollat ​​kuvan alkuun ja lopussa moninkertaistaa.

-Ensimmäisen numeron oikeanpuoleinen vähennys 10: stä ja tulos kaksinkertaistuu.

-Seuraavien numeroiden vähentyminen 9: stä tulos kaksinkertaistuu ja naapuri lisätään.

-Saavuttuaan nolla vähentämään 2 oikealta oikealta.

- Kertolasku 8: lla

Esimerkki kertolaskusta 8

-Kerro 789 8: lla

Kuva 6. Esimerkki Kuvan kertolasku 8: lla, Trachtenberg -menetelmän mukaan. Lähde: f. Zapata.

- Kertolasku 4: llä

-Lisää nollat ​​oikealle ja vasemmalle moninkertaistumisesta.

-Vähennä 10 yksikön vastaava numero lisäämällä 5, jos se on pariton numero.

-Vähennä 9: stä kunkin kerroksen muodossa, lisäämällä puolet naapurista oikealle ja jos se on pariton numero lisäämään 5 lisäksi.

-Saavuttuaan nollaan moninkertaisen paikan alussa puolet naapurin puolet paitsi yksi.

Esimerkki kertolaskusta 4

Kerro 365187 x 4

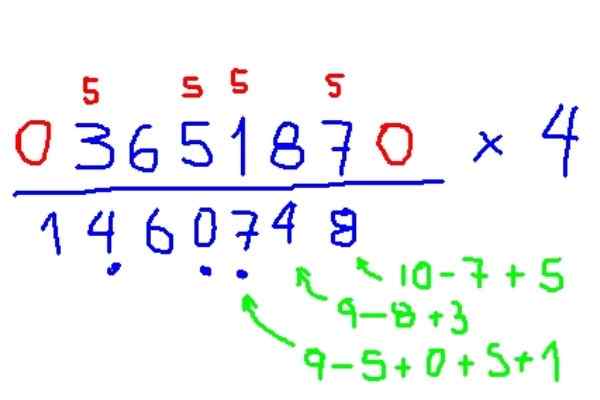Kuva 7. Esimerkki Kuvan kertolasku 4: llä, Trachtenberg -menetelmän mukaan. Lähde: f. Zapata.

- Kertolasku 3: lla

-Lisää nolla lisääntymisen kumpaankin päähän.

-Vähennä 10 paitsi yksikön numero ja lisää 5, jos se on pariton numero.

-Muiden numeroiden osalta vähennä 9 kopioi tulos, lisää puolet naapurista ja lisää 5, jos se on pariton.

-Saavuttuaan otsikon nolla, aseta koko puoli naapurin koko puoli miinus 2.

Esimerkki kertolaskusta 3

Kerro 2588 3: lla

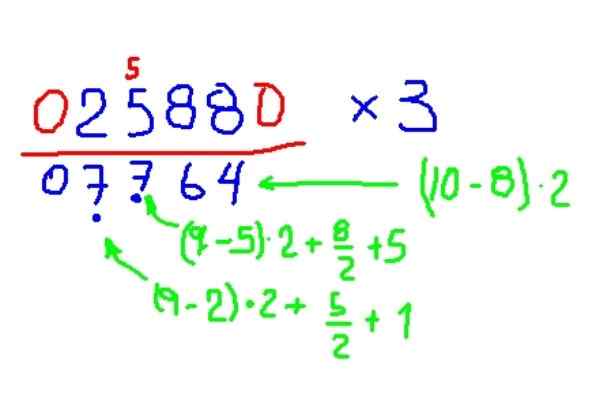Kuva 8. Esimerkki Kuvan kertolasku 3: lla, Trachtenberg -menetelmän mukaan. Lähde: f. Zapata.

- Kertolasku 2: lla

-Lisää nollat ​​päihin ja kaksinkertaista jokainen numero, jos ylität 10, lisää yksi seuraavaan.

Esimerkki kertolasku 2

Kerro 2374 2: lla

0 -23740 x 2

04748

Kerro yhdistelmäkuvioilla

Edellä mainittuja sääntöjä sovelletaan, mutta tulokset kulkevat vasemmalle kymmenien, satoja ja niin edelleen. Katsotaanpa seuraavaa esimerkkiä:

Harjoittele 

Kerro 37654 498: lla

0376540 x 498

301232 Sääntö 8

338886 sääntö 9: lle

150616 Sääntö 4: lle

18751692 Lopullinen summa

Viitteet

1. Cutler, Ann. 1960.Matematiikan perusjärjestelmä Trachtenbergin nopeusjärjestelmä. Doubleday & Co, NY.
2. Valhe. Nopea matematiikkajärjestelmä. Palautettu: Dialnet.com
3. Matemaattinen nurkka. Nopea kertolasku Trachtenbergin menetelmällä. Toipunut: Rinconmathematical.com
4. Matematiikan perusjärjestelmä Trachtenbergin nopeusjärjestelmä. Toipunut: Trachtenbergspeedmath.com
5. Wikipedia. Trachtenberg -menetelmä. Toipunut: Wikipedia.com