Orthoedro -kaavat, pinta -ala, tilavuus, diagonaali, esimerkkejä

Hän Ortoedro Se on tilavuus- tai kolmiulotteinen geometrinen hahmo, jolla on kuusi suorakulmaista kasvoja, niin että vastakkaiset kasvot ovat rinnakkaisissa tasoilla ja ovat identtisiä tai yhdenmukaisia ​​suorakulmioita toistensa kanssa toistensa kanssa. Toisaalta tietyn kasvojen vieressä olevat kasvot ovat kohtisuorassa olevissa tasoilla.

Sitä voidaan myös harkita milloin Ortoedro Ortogonaalisena suorakaiteen muotoisena perusprismina, jossa diHedros -kulmat Yhteisen reunan vieressä olevien kahden puolella olevan suunnitelman muodostama, ne mittaavat 90º. Kahden pinnan välinen kaksitahoinen kulma mitataan kohtisuoran ja yhteisen tason kasvojen risteyksessä.

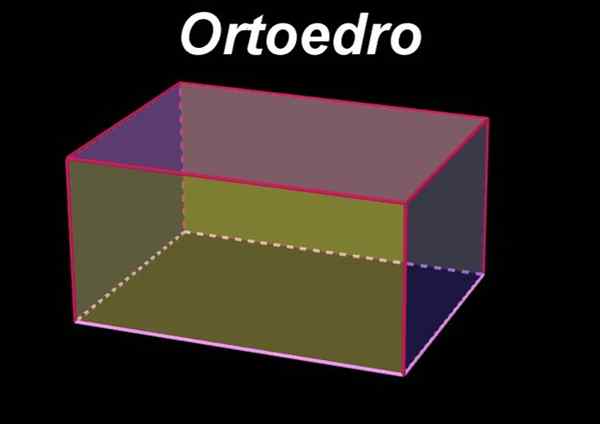
Kuvio 1. Ortoedro. Lähde: f. Zapata geogebralla.

Samoin ortoedro on a suorakulmio, Koska tämä on määritelty rinnakkaiskipille kuuden pinnan tilavuuskuvaksi, jotka ovat yhdensuuntaiset kaksi kahteen.

Kaikissa rinnakkaiskipiteissä kasvot ovat yhdensuuntaisia ​​ohjelmia, mutta suorakulmiossa rinnakkaispipejä kasvojen on oltava suorakaiteen muotoisia.

[TOC]

Ortodron osat

Polihedronin osat, kuten Orthoedro, ovat:

-Reunat

-Kärjet 

-Kasvot

Ortoedron pinnan kahden reunan välinen kulma on samaan aikaan kuin kahden muun reunan vieressä olevan kahden muun pinnan muodostaman kaksipuolisen kulman kanssa muodostaen oikean kulman. Seuraava kuva selventää jokaista konseptia:

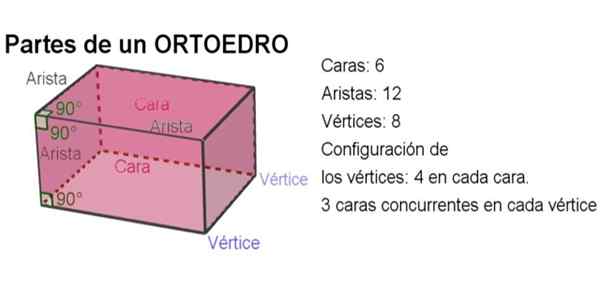Kuva 2. Osa ortoedrosta. Lähde: f. Zapata geogebralla.

-Kaiken kaikkiaan ortoedrossa on 6 kasvoja, 12 reunaa ja 8 kärkeä.

-Kahden reunan välinen kulma on oikea kulma.

-Kaupallinen kulma minkä tahansa kahden sivun välillä on myös suora.

-Kummassakin kasvossa on neljä kärkipistettä ja jokaisessa kärkipisteessä on kolme puolueetonta ortogonaalista kasvoja.

Voi palvella sinua: mikä on Capicúa -numero? Ominaisuudet ja esimerkit

Orthoedro -kaavat

Alue

A: n pinta tai alue Ortoedro Se on heidän kasvojensa alueiden summa.

Jos kärkipisteen yhdellä kolmella reunalla on mitat A, B ja C, kuten kuvassa 3 esitetään, niin etupinnalla on alue C⋅B Ja taustapinnassa on myös C⋅B -alue.

Sitten kahdella sivuttaisella kasvolla on alue A⋅B jokainen. Ja lopuksi, lattian ja katon kasvoilla on alue A⋅C jokainen.

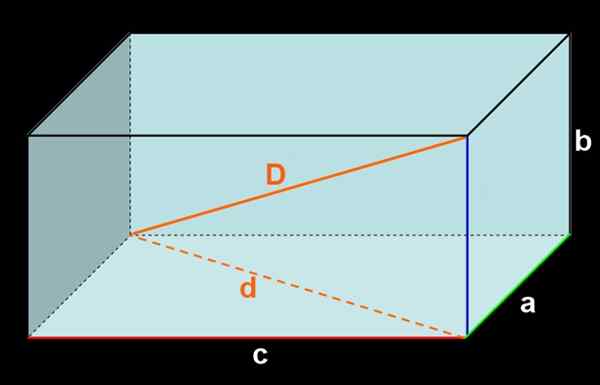Kuva 3. Ortoedro mitoista A, B, C. Sisäinen diagonaali D ja ulkoinen diagonaali D.

Kaikkien kasvojen alueen lisääminen saadaan:

A = 2⋅c⋅b + 2⋅ a⋅b + 2⋅a

Yleisen tekijän piirtäminen ja termien tilaaminen:

A = 2⋅ (a⋅b + b⋅c + c⋅a)

Tilavuus

Jos Orthoedroa pidetään prismana, sen tilavuus lasketaan seuraavasti:

Tilavuus = prisman pohjapinta -ala x prisman korkeus

Tässä tapauksessa mitat lattia otetaan suorakaiteen muotoiseksi c ja -lla, Joten perusalue on C⋅a.

Korkeus annetaan pituudella b - Ortogonaalisista reunoista sivuille -lla ja c.

Kertomalla pohjapinta -ala (A⋅C) korkeudella b - Sinulla on äänenvoimakkuus V Orthoedrosta:

V = a⋅b⋅c

Sisäinen diagonaali

Ortoedrossa on kahta tyyppiä diagonaaleja: ulkoiset diagonaalit ja sisäiset diagonaalit.

Ulkoiset diagonaalit ovat suorakaiteen muotoisilla kasvoilla, kun taas sisäiset diagonaalit ovat segmenttejä, jotka liittyvät kahteen vastakkaiseen kärkipisteeseen, jotka ymmärtävät vastakkaiset kärkipisteet, jotka eivät jaa mitään reunaa.

Ortoedrossa on neljä sisäistä diagonaalia, kaikki yhtä suuret mittaukset. Sisäisten diagonaalien pituus voidaan saada soveltamalla Pythagoras -lause suorakulmioihin.

Se voi palvella sinua: trigonometriset toiminnot: Basic, Cartesian tasossa, esimerkkejä, liikunta

Orthoedro -lattian ulkoisen diagonaalin pituus D täyttää Pythagoran suhteen:

d -d² = a² + c²

Samoin Pythagoran suhteen sisätilojen mittaus diagonaali:

D -d² = D² + b -².

Yhdistämällä kaksi aikaisempaa lauseketta, jotka sinulla on:

D -d² = a² + c² + b -².

Lopuksi, minkä tahansa Orthoedron sisäisen diagonaalin pituus annetaan seuraavalla kaavalla:

D = √ (a² + b -² + c² -A. 

Esimerkit

- Esimerkki 1

Mason rakentaa ortoedro -muotoisen säiliön, jonka sisäiset mitat ovat: 6 m x 4 m ja 2 m korkea. Sitä pyydetään:

a) Määritä säiliön sisäpinta, jos se on täysin avoin yläosassaan. 

b) Laske säiliön sisätilan tilavuus.

c) Löydä diagonaalin sisäpituus.

d) Mikä on säiliön kapasiteetti litrana?

Liittää jhk

Otamme suorakulmaisen pohjan A = 4 m ja c = 6 m ja korkeuden mitat b = 2 m

Ortoedron alue annetut mitat annetaan seuraavalla suhteella:

A = 2⋅ (a⋅b + b⋅c + c⋅a) = 2⋅ (4 m⋅2 m + 2 m⋅6 m + 6 m⋅4 m)

Tarkoittaen:

A = 2⋅ (8 m² + 12 m² + 24 m²) = 2⋅ (44 m²) = 88 m²

Aikaisempi tulos on ortoedron alue suljettu annetuilla mitoilla, mutta koska se on säiliö, joka on täysin löydetty sen yläosasta, säiliön sisäosien pinnan saamiseksi, puuttuvan kannen pinta -ala tuo on:

C⋅a = 6 m ⋅ 4 m = 24 m².

Lopuksi säiliön sisäpinta on: s = 88 m² - 24 m² = 64 m².

Ratkaisu b

Säiliön sisätilavuus annetaan säiliön sisämittaisten ortoedrojen tilavuudella:

V = a⋅b⋅c = 4 m ⋅ 2 m ⋅ 6 m = 48 m³.

Liuos C

Oktareedronin sisävioginaalilla säiliön sisätilojen mitat ovat antaneet:

Voi palvella sinua: jatkuva satunnaismuuttuja

√ (a² + b -² + c² ) = √ ((4 m)² + (2 m)² + (6 m)² -A

Suorittamalla ilmoitetut toiminnot:

D = √ (16 m² + 4 m² + 36 m² ) = √ (56 m²) = 2√ (14) m = 7,48 m.

Liuos D

Tankin säiliön kapasiteetin laskemiseksi on tarpeen tietää, että kuutiometrin tilavuus vastaa litran kapasiteettia. Se oli aikaisemmin laskettu tilavuutena kuutiometreinä, mutta se on muutettava kuutiometriin ja sitten litreiksi:

V = 48 m³ = 48 (10 dm)³ = 4.800 DM³ = 4.800 L

- Harjoitus 2

Lasi -akvaarion kuutiomuoto on 25 cm. Määritä alue m², Litran tilavuus ja diagonaalin sisäpituus CM: ssä.

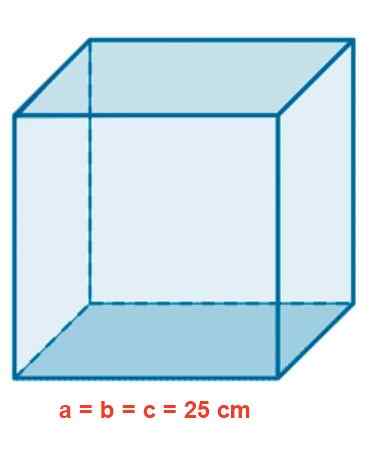Kuva 4. Kuutiolasi -akvaario.

Ratkaisu

Alue lasketaan samalla Orthoedro -kaavalla, mutta ottaen huomioon, että kaikki mitat ovat identtisiä:

A = 2⋅ (3 a⋅a) = 6⋅ a² = 6⋅ (25 cm)² = 1.250 cm²

Kuution tilavuus on annettu:

V = a³ = (25 cm)³ = 15.625 cm³ = 15.625 (0,1 dm)³ = 15 625 DM³ = 15,625 l.

Sisätalojen pituus D on:

D = √ (3²) = 25√ (3) cm = 43,30 cm.

Viitteet

1. Arias j. Geogebra: Prisma. Palautettu: YouTube.com.
2. Laskeminen.DC. Harjoitukset ja ongelmat, jotka on ratkaistu alueille ja tilavuuksille. Palautettu: laskelma.DC.
3. Salvador r. Pyramid + Orthoedro geogebralla (IHM). Palautettu: YouTube.com
4. Weisstein, Eric. "Ortoedro". Matematiikka. Wolfram -tutkimus.
5. Wikipedia. Ortoedro. Palautettu: on.Wikipedia.com