Lineaarinen ohjelmointi mihin se on, mallit, rajoitukset, sovellukset

Se lineaarinen ohjelmointi Se on matemaattinen menetelmä, jonka tarkoituksena on optimoida (maksimoida tai minimoida tarpeen mukaan) funktio, jonka muuttujat ovat rajoituksia, niin kauan kuin funktio ja rajoitukset ovat lineaarisesti riippuvaisia ​​muuttujista.

Yleensä toiminto käytännön tilanteen optimoimiseksi, kuten valmistajan voitto, jonka panokset, työvoima tai koneet ovat rajoitetut.

Kuvio 1. Lineaarista ohjelmointia käytetään laajasti voittojen optimointiin. Lähde: Piqsels.

Yksi yksinkertaisimmista tapauksista on lineaarinen funktio maksimoida, joka riippuu vain kahdesta muuttujasta, joita kutsutaan Päätösmuuttujat. Se voi olla muoto:

Z = k₁x + k₂ja

K: n kanssa₁ ja k₂ vakiot. Tämä toiminto tunnetaan nimellä Objektiivitoiminto. Tietenkin on tilanteita, jotka ansaitsevat enemmän kuin kaksi muuttujaa heidän tutkimukselleen, ja ne ovat monimutkaisempia:

Z = k₁x₁ + k -k -₂x₂ + k -k -₃x₃ +.. .

Ja rajoitukset on myös matemaattisesti mallinnettu yhtälöjärjestelmän tai eriarvoisuuden kautta, yhtä lineaarisesti x ja ja.

Tämän järjestelmän ratkaisuja kutsutaan toteutettavissa olevat ratkaisut jompikumpi toteutettavissa olevat kohdat. Ja toteutettavissa olevien pisteiden joukossa on ainakin yksi, joka optimoi objektiivifunktion.

Lineaarinen ohjelmointi kehitti itsenäisesti amerikkalainen fyysikko ja matemaatikko.

Ongelmanratkaisumenetelmä, joka tunnetaan nimellä Simplex -menetelmä Se on Dantzigin perustaminen, joka työskenteli Yhdysvaltain ilmavoimissa, Berkeleyn yliopistossa ja Stanfordin yliopistossa.

Kuva 2. Matemaatikot George Dantzig (vasen) ja Leonid Kantorovich (oikea). Lähde: f. Zapata.

[TOC]

Lineaariset ohjelmointimallit

Tarvittavat elementit lineaarisen ohjelmointimallin perustamiseksi, jotka sopivat käytännön tilanteeseen, ovat:

-Objektiivitoiminto

-Päätösmuuttujat

-Rajoitukset

Objektiivisessa toiminnossa mitä haluat saavuttaa, on määritelty. Oletetaan esimerkiksi, että halutaan maksimoida tiettyjen tuotteiden valmistuksesta saadut voitot. Sitten "voitto" -toiminto on vahvistettu, sen hinnan mukaan, jolla tuotteet myydään.

Matemaattisesti tämä funktio voidaan ilmaista lyhennetyllä summauksella:

Z = ∑k_Yllyttää x_Yllyttää

Tässä yhtälössä k_Yllyttää Ne ovat kertoimia ja x_Yllyttää Ovatko päätöksenteon muuttujat.

Päätösmuuttujat ovat järjestelmän elementtejä, joiden hallinta on ja niiden arvot ovat positiivisia todellisia lukuja. Ehdotetussa esimerkissä päätöksenteon muuttujat ovat kunkin valmistettavan tuotteen määrä enimmäisvoittoa varten.

Lopuksi meillä on rajoituksia, jotka ovat lineaarisia yhtälöitä tai epätasa -arvoisia päätöksentekomuuttujien suhteen. Ne kuvaavat ongelman rajoituksia, jotka tunnetaan ja voivat olla esimerkiksi valmistuksessa käytettävissä olevat raaka -aineiden määrät.

Voi palvella sinua: korkeampi kuin kahden toiminnot (esimerkit)

Rajoitustyypit

Sinulla voi olla määrä M -rajoituksia, alkaen J = 1 siihen asti kun J = m. Matemaattisesti rajoitukset ovat kolmen tyyppisiä:

1. -Lla_{J -} = ∑ a_ij . x_Yllyttää
2. B -_{J -} ≥ ∑ b_ij . x_Yllyttää
3. C_{J -} ≤ ∑ c_ij . x_Yllyttää

Ensimmäinen rajoitus on lineaarista yhtälötyyppiä ja tarkoittaa, että arvo_{J -}, jota tiedetään, on kunnioitettava.

Jäljellä olevat kaksi rajoitusta ovat lineaarisia eriarvoisuuksia ja tarkoittaa, että B -arvot_{J -} ja c_{J -}, tunnetaan, voidaan kunnioittaa tai voittaa, kun ilmestyvä symboli on ≥ (suurempi tai yhtä suuri) tai kunnioittaa tai ei voitettu, jos symboli on ≤ (vähemmän tai yhtä suuri).

Malliesimerkki

Sovelluskentät ovat hyvin monimuotoisia, jotka kattavat liiketalouden ravitsemukseen, mutta menetelmän ymmärtämiseksi ehdotetaan yksinkertainen malli käytännöllisestä tilanteesta kahdella muuttujalla.

Paikallinen leivonnainen tunnetaan kahdesta erikoisuudesta: musta viidakon kakku ja Sacrista -kakku.

Laadinnoissaan ne vaativat munia ja sokeria. Mustalle viidakkolle tarvitaan 9 munaa ja 500 g sokeria, kun taas 8 munaa ja 800 g sokeria ovat välttämättömiä sacripeniinille. Vastaavat myyntihinnat ovat 8 dollaria ja 10 dollaria.

Ongelmana on: kuinka monta kunkin tyypin kakkua leivonnaiset saavat tehdä maksimoimaan sen voiton, tietäen, että siinä on 10 kiloa sokeria ja 144 munaa?

Päätösmuuttujat

Päätösmuuttujat ovat "x" ja "y", jotka suhtautuvat todellisiin arvoihin:

-X: Musta viidakon kakkujen määrä

-Y: Sacriphantine -tyyppiset kakut.

Rajoitukset

Rajoitukset annetaan sillä, että kakkujen lukumäärä on positiivinen määrä ja raaka -aineiden määrät on rajoitettua.

Siksi matemaattisella tavalla nämä rajoitukset hankkivat lomakkeen:

1. x ≥ 0
2. ja ≥0
3. 9x +8y ≤ 144
4. 0 -.5 x + 0.8 ja ≤ 10

Rajoitukset 1 ja 2 muodostavat Ei -negatiivisuusolosuhteet Aikaisemmin paljastettu ja kaikki nostetut eriarvoisuudet ovat lineaarisia. Rajoituksissa 3 ja 4 ovat arvoja, joita ei pidä ylittää: 144 munaa ja 10 kg sokeria.

Objektiivitoiminto

Lopuksi, objektiivifunktio on voitto, joka saadaan valmistuksella “x” määrää mustia viidakon kakkuja plus “y” sakristiinien määrä. Se on rakennettu kertomalla hinta valmistettujen kakkujen määrällä ja lisäämällä jokaiselle tyypille. Se on lineaarinen funktio, jota kutsumme g (x, y):

G = 8x + 10y

Ratkaisumenetelmät

Eri ratkaisumenetelmien joukossa ovat graafiset menetelmät, simplex -algoritmi ja sisäpisteen menetelmä, mainita.

- Graafinen tai geometrinen menetelmä

Kun sinulla on ongelma kahdesta muuttujasta, kuten edellisestä osasta, rajoitukset määrittävät monikulmion alueen tasossa Xy, puhelu toteutettavissa oleva alue jompikumpi Elinkelpoisuusalue.

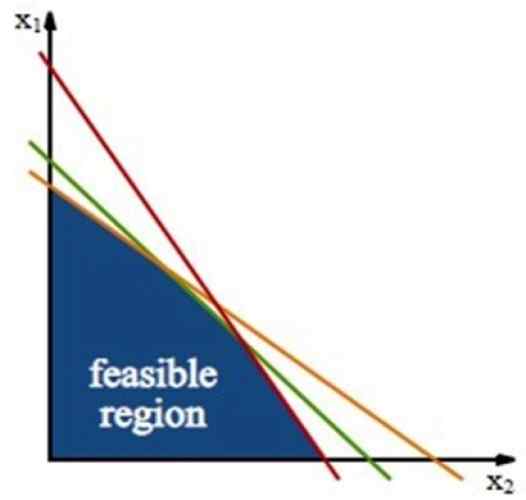Kuva 3. Toteutettavissa oleva alue, jolla optimointiongelman ratkaisu sijaitsee. Lähde: Wikimedia Commons.

Tämä alue on rakennettu läpi Rajoituslinjat, jotka ovat rajoitusten eriarvoisuuksista saatuja viivoja, jotka työskentelevät vain tasa -arvon merkin kanssa.

Voi palvella sinua: äärellinen sarja: Ominaisuudet, esimerkit, ratkaisut harjoitukset

Leipomon tapauksessa, joka haluaa optimoida voitot, rajoituslinjat ovat:

1. x = 0
2. y = 0
3. 9x +8y = 144
4. 0 -.5 x + 0.8y = 10

Kaikki näiden linjojen lukitut alueen kohdat ovat mahdollisia ratkaisuja, joten niitä on ääretön. Lukuun ottamatta siinä tapauksessa, että toteutettavissa oleva alue on tyhjä, jolloin esiin nousevassa ongelmassa puuttuu ratkaisu.

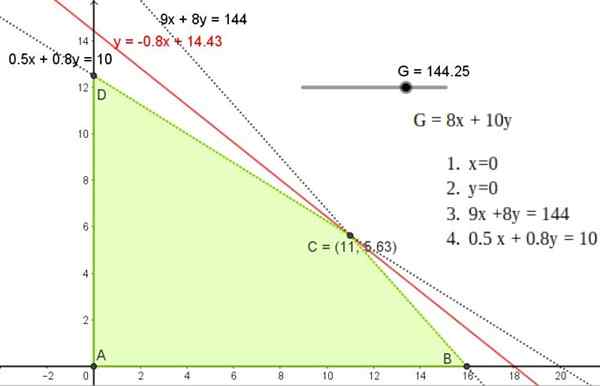
Onneksi leivonnaisongelman vuoksi toteutettavissa oleva alue ei ole tyhjä, meillä on se alla.

Kuva 4. Leivonnaisongelman toteutettavissa oleva alue. Suora linja 0 ylittää alkuperä. Lähde: f. Zapata geogebralla.

Optimaalinen ratkaisu, jos se on olemassa, on objektiivisen toiminnon avulla. Esimerkiksi, kun kyse on maksimaalisen G -vahvistuksen löytämisestä, sinulla on seuraava rivi, jota kutsutaan Iso-benefice Suora-

G = k₁x + k₂ja → y = -k₁x / k₂ + G/ k₂

Tällä linjalla saadaan kaikki parit (x, y), jotka tarjoavat tietyn voiton G, joten G: n arvon mukaan on olemassa linjojen perhe, mutta kaikilla on sama kaltevuus -K₁ / k₂, niin että ne ovat yhdensuuntaisia ​​suorat.

Optimaalinen liuos

Nyt voidaan osoittaa, että lineaarisen ongelman optimaalinen ratkaisu on aina toteutettavan alueen äärimmäinen tai kärki. Niin:

Linjaliuos on kauimpana alkuperästä ja jolla on ainakin yksi yhteinen kohta toteutettavissa olevan alueen kanssa.

Jos lähtöä lähinnä olevalla linjalla on kokonainen segmentti, joka on yhteinen toteutettavissa olevan alueen kanssa, sanotaan, että on olemassa äärettömiä ratkaisuja. Tämä tapaus tapahtuu, jos ISO-hyötyviivan kaltevuus on yhtä suuri kuin minkä tahansa muun alueen rajoittavan linjan.

Leivonnallemme ehdokkaiden kärkipisteet ovat A, B ja C.

- Simplex Dantzigin menetelmä

Graafista tai geometristä menetelmää voidaan soveltaa kahdelle muuttujalle. Se on kuitenkin monimutkaisempaa, kun muuttujia on kolme, ja mahdotonta käyttää suurempaan määrään muuttujia.

Kun kyse on useamman kuin kahden muuttujan ongelmista, Simplex -menetelmä, joka koostuu sarjasta algoritmeja objektiivifunktioiden optimoimiseksi. Yksinkertaisia ​​matriiseja ja aritmeettista käytetään yleensä laskelmien suorittamiseen.

Simplex -menetelmä alkaa valitsemalla toteutettavissa oleva ratkaisu ja tarkistamalla, onko se optimaalinen. Jos se on, olemme jo ratkaisseet ongelman, mutta jos se ei ole, se jatkuu kohti ratkaisua lähempänä optimointia. Jos liuos on olemassa, algoritmi sen kanssa muutamassa yrityksessä.

Voi palvella sinua: mikä on tilastoalue? (Esimerkkejä)

Sovellukset

Monilla aloilla sovellettu lineaarinen ja epälineaarinen ohjelmointi parhaiden päätösten tekemiseksi kustannusten vähentämisessä ja voittojen lisäämisessä, jotka eivät aina ole rahallisia, koska ne voidaan mitata ajoissa, jos haluat minimoida tarvittava aika suorittaa Sarja operaatioita.

Tässä on joitain kenttiä:

-Markkinoinnissa sitä käytetään löytämään paras mediayhdistelmä (sosiaaliset verkostot, televisio, lehdistö ja muut) tietyn tuotteen mainostamiseen.

-Yrityksen tai tehtaan henkilöstölle sopivan työn jakamiseen tai heidän aikatauluihin heille.

-Ravitsevimman ruoan valinnassa ja karjan ja siipikarjateollisuuden alhaisimmilla kustannuksilla.

Ratkaisut

- Harjoitus 1

Kuvaavat edellisissä osissa nostettu lineaarinen ohjelmointimalli.

Ratkaisu

On välttämätöntä kuvaava arvojoukko, joka määritetään ongelmassa määritellyllä rajoitusjärjestelmällä:

1. x ≥ 0
2. ja ≥0
3. 9x +8y ≤ 144
4. 0 -.5 x + 0.8 ja ≤ 10

Erotuurioiden 1 ja 2 antama alue vastaa Cartesian lentokoneen ensimmäistä kvadranttia. Ero -arvioinnissa 3 ja 4 se alkaa löytämällä rajoituslinjat:

9x +8y = 144

0 -.5 x + 0.8y = 10 → 5x + 8y = 100

Mahdollinen alue on nelikulmainen, jonka kärkipisteet ovat pisteitä A, B, C ja D.

Vähimmäisvahvistus on 0, joten 8x + 10 ja 10 -rivi on alaraja ja ISO -benefit -viivat ovat vireillä -8/10 = -0.8.

Tämä arvo on erilainen kuin muiden rajoituslinjojen rinteet ja koska toteutettavissa oleva alue on rajoitettu, on ainutlaatuinen ratkaisu.

Kuva 5. Harjoituksen 1 graafinen ratkaisu, joka näyttää toteutettavan alueen ja pistiliuoksen C yhdessä mainitun alueen kärjessä. Lähde: f. Zapata.

Tämä ratkaisu vastaa kaltevuusviivaa -0.8, joka kulkee yhden pisteistä A, B tai C, jonka koordinaatit ovat:

A (11; 5.625)

B (0; 12.5)

C (16, 0)

Optimaalinen ratkaisu

Laskemme G: n arvon jokaiselle näistä kohdista:

-(11; 5.625): g_-Lla = 8 x 11 + 10 x 5.625 = 144.25

-(0; 12.5): G_{B -} = 8 x 0 + 10 x 12.5 = 125

-(16, 0): G_C = 8 x 16 + 10 x 0 = 128

Suurin voitto on 11 mustaa viidakon kakkua ja 5.625 Sacripantiinikakkua. Tämä ratkaisu on yhtä mieltä ohjelmiston kautta löydetyn kanssa.

- Harjoitus 2

Varmista edellisen harjoituksen tulos käyttämällä useimmissa laskentataulukoita, kuten Excel tai Calc de LibreOffice, joka sisältää simplex -algoritmin lineaariseen ohjelmoinnin optimointiin.

Ratkaisu

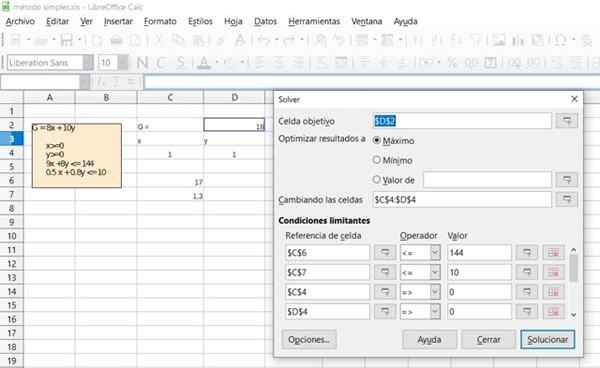Kuva 6. Yksityiskohta harjoituksen 1 ratkaisusta ilmaisen toimistolaskentataulukon kautta. Lähde: f. Zapata. 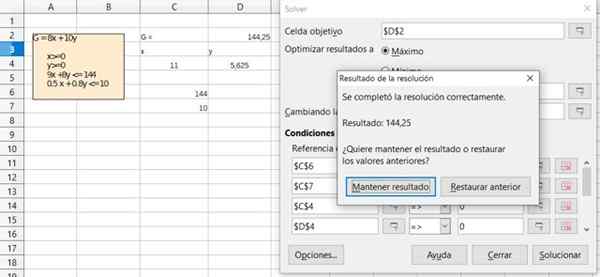Kuva 7. Yksityiskohta harjoituksen 1 ratkaisusta ilmaisen toimistolaskentataulukon kautta. Lähde: f. Zapata.

Viitteet

1. Loistava. Lineaarinen ohjelmointi. Toipunut: loistava.org.
2. Eppen, G. 2000. Operaatiotutkimus hallinnollisessa tieteessä. Viides. Painos. Prentice Hall.
3. Haeussler, E. 1992. Matematiikka hallinto- ja taloustieteelle. Toinen. Painos. Ibero -meralainen toimitusryhmä.
4. Vuokra.Eus. Lineaarinen ohjelmointi. Toipunut: Hiru.Eus.
5. Wikipedia. Lineaarinen ohjelmointi. Palautettu: on. Wikipedia.org.