Omaisuusomaisuuden todistus, esimerkkejä

Se Algebra -lukitusominaisuus Se on ilmiö, joka yhdistää operaation kaksi elementtiä, joissa tarvittava ehto on, että mainitun operaation 2 elementin jälkeen tulos kuuluu myös alkuperäiseen joukkoon.

Esimerkiksi, jos paritonta numeroa otetaan kokonaisuutena ja summa operaationa, saadaan mainitun joukon lukko,. Tämä johtuu siitä, että 2 parillisen numeron summa annetaan aina seurauksena toinen numero, mikä täyttää lukitusolosuhteet.

Lähde: Unspash.com

[TOC]

Ominaisuudet

On monia ominaisuuksia, jotka määrittävät algebralliset tilat tai rungot, kuten rakenteet tai renkaat. Lock -ominaisuus on kuitenkin yksi tunnetuimmista algebrassa.

Kaikkien näiden ominaisuuksien sovellukset eivät perustu ilmiöihin tai numeerisiin elementteihin. Monet päivittäiset esimerkit voivat toimia algebrallisesta teoreettisesta lähestymistavasta puhdasta.

Esimerkki voi olla maan kansalaiset, joissa on muun muassa oikeussuhde, kuten kaupallinen tai avioliitto. Tämän operaation tai johdon jälkeen he ovat edelleen maan kansalaisia. Siten kansalaisuus- ja hallintatoiminnot kahdesta kansalaisesta edustavat lukkoa.

Numeerinen algebra

Numeroiden suhteen on monia näkökohtia, jotka ovat olleet syytä tutkimukseen matematiikan ja algebran eri virroissa. Näistä tutkimuksista on syntynyt suuri joukko aksioomeja ja lauseita, jotka toimivat nykyajan tutkimuksen teoreettisena perustana ja teoksissa.

Jos työskentelet numeeristen sarjojen kanssa, voimme luoda toisen voimassa olevan määritelmän lukitusominaisuudelle. Sanotaan.

Voi palvella sinua: jakava omaisuus

Esittely

Lukon esittelyä käytetään elementteihin ja toimintoihin, jotka ovat läsnä Real N -numeroissa.

Olkoon A ja B kaksi numeroa, jotka kuuluvat joukkoon r, näiden elementtien lukko on määritelty jokaiselle R -sisälle olevalle toiminnalle.

Lisäys

- Summa: ∀ A ˄ B ∈ R → A + B = C ∈ R

Tämä on algebrallinen tapa sanoa se Kaikille a ja b: lle, joka kuuluu reaalilukuihin.

On helppo tarkistaa, onko tämä ehdotus totta; Riittää, jotta voidaan tehdä minkä tahansa todellisen numeron välinen summa ja varmista, kuuluuko tulos myös reaalilukuihin.

3 + 2 = 5 ∈ R

-2 + (-7) = -9 ∈ R

-3 + 1/3 = -8/3 ∈ R

5/2 + (-2/3) = 11/6 ∈ R

On havaittu, että lukkoolosuhteet täyttyvät todellisille numeroille ja summalle. Tällä tavalla se voidaan päätellä: Reaalilukujen summa on algebrallinen lukko.

Kertolasku

- Kertolasku: ∀ A ˄ B ∈ R → A . B = c ∈ R

Kaikille a ja b: lle, jotka kuuluvat todellisiin, A: n kertominen B: lle on yhtä suuri kuin C, joka kuuluu myös todelliseen.

Kun tarkistetaan edellisen esimerkin samoilla elementeillä, seuraavat tulokset havaitaan.

3 x 2 = 6 ∈ R

-2 x (-7) = 14 ∈ R

-3 x 1/3 = -1 ∈ R

5/2 x (-2/3) = -5/3 ∈ R

Tämä on riittävä näyttöä päätelläkseen, että: Todellisten lukujen kertominen on algebrallinen lukko.

Tätä määritelmää voidaan laajentaa kaikkiin reaalilukujen operaatioihin, vaikka löydämme tiettyjä poikkeuksia.

Lähde: Pixabay.com

Erityistapaukset R: ssä

Jako

Erityisesti jaostoa havaitaan, jos seuraavaa poikkeusta arvostetaan:

Voi palvella sinua: Klassinen todennäköisyys: Laskenta, esimerkit, ratkaisut harjoitukset

∀ A ˄ B ∈ R → A / B ∉ R ↔ B = 0

Kaikille A ja B, jotka kuuluvat R - Sen on oltava B: n välillä.

Tämä tapaus viittaa rajoituksiin, jotka eivät pysty jakamaan nollan välillä. Koska nolla kuuluu todellisiin numeroihin, niin on päätelty, että: lensJako ei ole lukko todellisessa.

Radio

Siellä on myös potentiaatiotoimenpiteitä, erityisesti arkistointia, joissa poikkeuksia esitetään vääntömomentin radikaalien voimista:

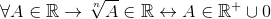; N: n kanssa

Kaikesta, johon se kuuluu kuninkaalle.

Tällä tavoin tarkoitetaan, että tasaiset juuret koskevat vain positiivisia todellisia ja on päätelty, että potentiaatio ei ole lukko r.

Logaritmi

Se on hyväksytty logaritmiselle funktiolle, jota ei ole määritelty pienempien tai yhtäläisten arvoille kuin nolla. Jos haluat tarkistaa, onko logaritmi R -lukko, etenee seuraavasti:

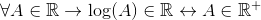
Kaikelle, johon se kuuluu reagoihin, a: n logaritmi kuuluu reagoihin, jos ja vain jos se kuuluu positiiviseen todelliseen.

Kun negatiiviset ja nolla -arvot, jotka myös kuuluvat R: hen jätetään pois, voidaan vahvistaa, että:

Logaritmi ei ole todellisten lukujen lukko.

Esimerkit

Tarkista luonnollisten lukujen summan ja vähentämisen lukko:

Summa n

Ensinnäkin on tarkistaa annetun sarjan eri elementtien lukitusolosuhteet, jos jos havaitaan, että jotkut elementit rikkovat ehdon, lukon olemassaolo voidaan kieltää automaattisesti.

Voi palvella sinua: lähentymisradio: Määritelmä, esimerkit ja harjoitukset ratkaistu

Tämä ominaisuus saavutetaan kaikille mahdollisille A- ja B -arvoille, kuten seuraavissa operaatioissa havaitaan:

1 + 3 = 4 ∈ N

5 + 7 = 12 ∈ N

1000 + 10000 = 11000 ∈ N

Ei ole luonnollisia arvoja, jotka rikkovat lukitusolosuhteita, joten se on saatu päätökseen:

Summa on lukko n.

Vähennä n

Luonnollisia elementtejä pyydetään murtamaan tilan; A - B kuuluu alkuperäiskansoille.

Käyttämällä on helppo löytää pareja luonnollisia elementtejä, jotka eivät täytä lukitusolosuhteita. Esimerkiksi:

7 - 10 = -3 ∉ a n

Tällä tavalla voimme päätellä, että:

Vähennys ei ole luonnollisten lukujen joukko.

Ehdotetut harjoitukset

1-asennus.

2-Explain, jos reaalilukujoukko on koko koko lukko.

3-määrite, mikä numeerinen joukko voi olla reaalilukun lukitus.

4-näyte kuvitteellisten lukujen lukitusominaisuus suhteessa summaan, vähentämiseen, kertolaskuun ja jakoon.

Viitteet

1. Puhtaan matematiikan panoraama: Bourbakist Choice. Jean Dieudonné. Reverte, 1987.
2. Algebrallisten lukujen teoria. Alejandro J. Díaz Barriga, Ana Irene Ramírez, Francisco Tomás. Meksikon kansallinen autonominen yliopisto, 1975.
3. Lineaarinen algebra ja sen sovellukset. Sandra Ibeth Ochoa García, Eduardo Gutiérrez González.
4. Algebralliset rakenteet V: Kehon teoria. Héctor a. Merklen. Amerikan osavaltioiden organisaatio, yleinen sihteeristö, 1979.
5. Johdanto kommutatiiviseen algebraan. Michael Francis Atiyah, I. G. Macdonald. Reverte, 1973.